এ অধ্যায়ের পাঠ্যসূচী।
- উপবৃত্ত (Ellipse)
- উপবৃত্তের প্রমিত সমীকরণ (Standard equation of Ellipse)
- উপবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ (Identifying the standard equation of an ellipse)
- উপবৃত্তের সমীকরণ সনাক্তকরণ (Identifying the equation of an ellipse)
- উপবৃত্তের ক্ষেত্রফল (Area of ellipse)
- উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর (Equation of the ellipse whose Major axis along \(x\) axis)
- উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর (Equation of the ellipse whose Major axis along \(y\) axis)
- নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর (Equation of an ellipse with fixed center whose major axis is along the \(x\) axis)
- নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর (Equation of an ellipse with fixed center whose major axis is along the \(y\) axis)
- \(y=mx+c\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত (The condition of the straight line \(y=mx+c\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\))
- \(x\cos\alpha + y\sin\alpha=p\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত (The condition of the straight line \(x\cos\alpha + y\sin\alpha=p\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\))
- \(lx+my+n=0\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত (The condition of the straight line \(lx+my+n=0\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\))
- উপবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান (The relative position of a point with respect to the ellipse)
- উপবৃত্তের উপরিস্থিত নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকর (Equation of the tangent at a given point on the ellipse)
- উপবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা (Focus and directrix of Ellipse)
- উপবৃত্তের বৃহদাক্ষ ও ক্ষুদ্রাক্ষের দৈর্ঘ্য (Major and Minor axis of Ellipse)
- উপবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা (Eccentricity from the equation of ellipse)
- উপবৃত্তের সমীকরণ থেকে উৎকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ (The co-ordinates of focus and the equation of directrix from the equation of ellipse)
- উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য (From the equation of an ellipse Latus rectum and it's length)
- উপবৃত্তের উপরিস্থিত কোনো বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান (Sum of the two epicentral distance of a point on the ellipse is equal to the length of Major axis)
- উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক যখন \((a\gt{b})\)(Parametric coordinates of a given point on the ellipse when \((a\gt{b})\))
- উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক যখন \((a\lt{b})\) (Parametric coordinates of a given point on the ellipse when \((a\lt{b})\))
- উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর লেখচিত্র (Graph of equation of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\))
- অধ্যায় \(6B\)-এর উদাহরণসমুহ
- অধ্যায় \(6B\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(6B\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(6B\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(6B\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
উপবৃত্ত
Ellipse
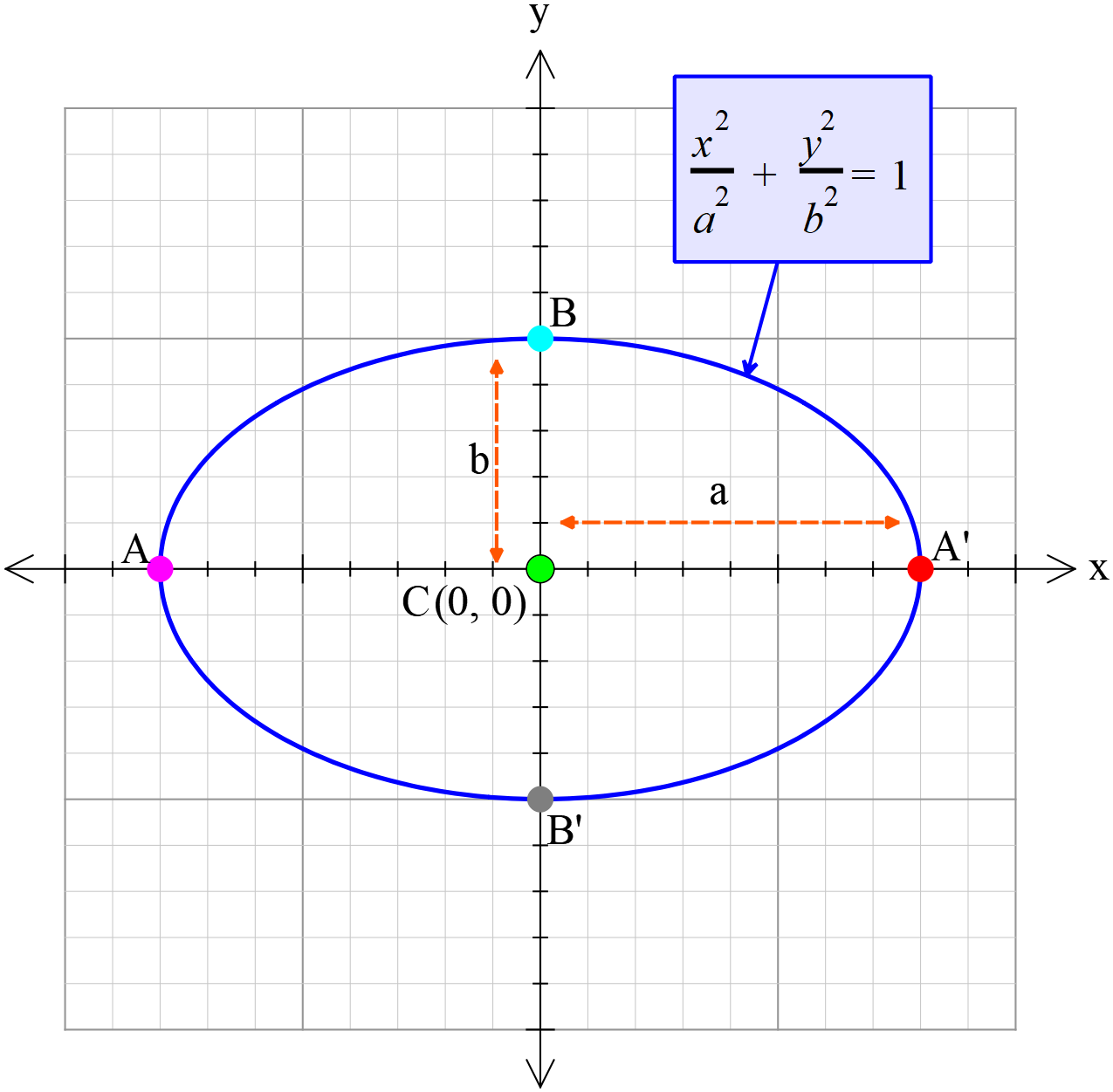উপবৃত্তঃ কোনো কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্ব দূরত্বের অনুপাত একটি স্থির রাশি এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা ক্ষুদ্রতর, তবে ঐ বিন্দুর সঞ্চারপথকে উপবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \(1\gt{e}\gt{0}\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত উপবৃত্তের সর্ববৃহত রেখাংশ \(AA^{\prime}\) কে বৃহৎ অক্ষ (Major axis) বলা হয়। বৃহদাক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(BB^{\prime}\) কে ক্ষুদ্র অক্ষ (Minor axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র এবং বৃহদাক্ষের প্রান্ত বিন্দু দুইটিকে শীর্ষবিন্দু বলা হয়। উপবৃত্তের প্রমিত সমীকরণ
Standard equation of Ellipse
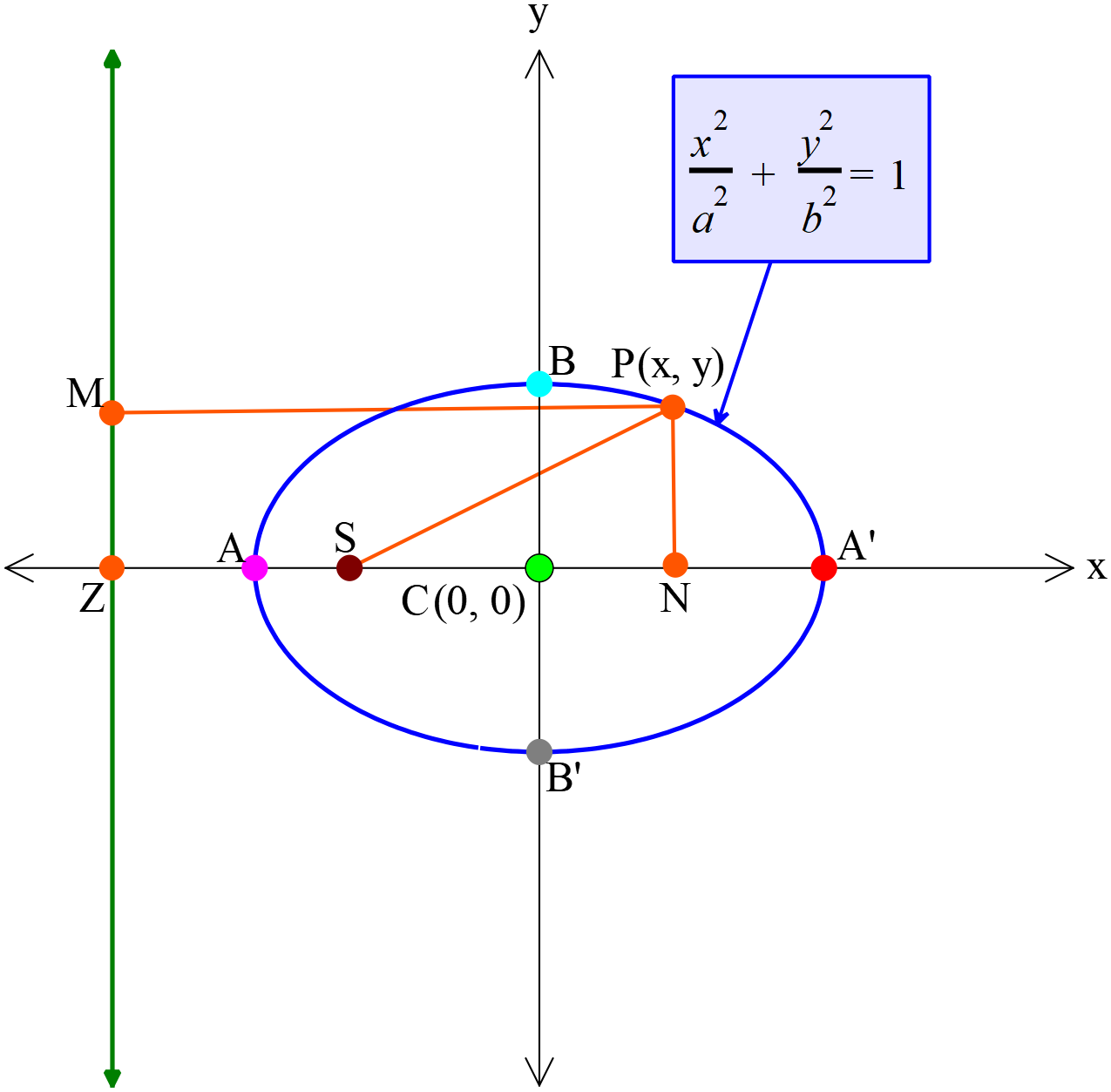
ধরি,উপবৃত্তের উপকেন্দ্র \(S\) নিয়ামকরেখা \(MZ\) এবং উৎকেন্দ্রিকতা \(1\gt{e}\gt{0},\) নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি। \(SZ\) রেখাকে \(A\) ও \(\acute A\) বিন্দুদ্বয় \(e:1\) অনুপাতে যথাক্রমে অন্তর্বিভক্ত ও বহিঃর্বিভক্ত করে, যেন \(SA=e.AZ\) এবং \(S\acute A=e.\acute AZ\)।
তাহলে, \(A\) ও \(\acute A\) উপবৃত্তের উপর দুইটি বিন্দু অর্থাৎ শীর্ষবিন্দু।
মনে করি \(A\acute A\)-এর মধ্যবিন্দু \(C\) এবং \(A\acute A=2a\)
তাহলে,\(CA=C\acute A=a\)
এখন,
\(SA=e.AZ\)
\(\therefore a-CS=e(CZ-a) .......(1)\) ➜ \(\because SA=CA-CS=a-CS; AZ=CZ-CA=CZ-a\)
এবং \(S\acute A=e.\acute AZ\)
\(\therefore a+CS=e(CZ+a) ........(2)\) ➜ \(\because S\acute A=C\acute A+CS=a+CS; \acute AZ=CZ+CA=CZ+a\)
\((1)\) ও \((2)\) যোগ করে,
\(a-CS+a+CS=e(CZ-a)+e(CZ+a)\)
\(\Rightarrow 2a=e(CZ-a+CZ+a)\)
\(\Rightarrow 2a=e.2CZ\)
\(\Rightarrow a=e.CZ\)
\(\Rightarrow e.CZ=a\)
\(\therefore CZ=\frac{a}{e}\)
\((2)\) - \((1)\)-এর সাহায্যে,
\(a+CS-a+CS=e(CZ+a)-e(CZ-a)\)
\(\Rightarrow 2CS=e(CZ+a-CZ+a)\)
\(\Rightarrow 2CS=e.2a\)
\(\Rightarrow CS=e.a\)
\(\therefore CS=ae\)
\(C\)-কে মূলবিন্দু , \(CX\) ও \(CY\)-কে যথাক্রমে \(x\)-অক্ষ ও \(y\)-অক্ষ বিবেচনা করি। উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(P\) বিন্দু হতে \(A\acute A\)-এর উপর \(PN\) ও নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি।
সুতরাং উপবৃত্তের সংজ্ঞানুসারে, \(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=NZ\)
\(\Rightarrow SP^2=e^2.NZ^2\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow SN^2+PN^2=e^2(CN+CZ)^2\) ➜ \(\because SP^2=SN^2+PN^2; NZ=CN+CZ\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(x+\frac{a}{e}\right)^2\) ➜ \(\because SN=CS+CN=ae+x; NZ=x+\frac{a}{e}\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(\frac{ex+a}{e}\right)^2\)
\(\Rightarrow (ae+x)^2+y^2=e^2.\frac{(ex+a)^2}{e^2}\)
\(\Rightarrow (ae+x)^2+y^2=(ex+a)^2\)
\(\Rightarrow a^2e^2+2aex+x^2+y^2=e^2x^2+2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex+a^2-a^2e^2-2aex\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2(1-e^2)}{a^2(1-e^2)}+\frac{y^2}{a^2(1-e^2)}=1\) ➜ উভয় পার্শ্বে \(a^2(1-e^2)\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1 .......(3)\)
\((3)\) নং সমীকরণে \(x=0\) বসিয়ে,
\(\frac{0^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow 0+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow y^2=a^2(1-e^2)\)
\(\Rightarrow y=\pm \sqrt{a^2(1-e^2)}\)
\(\therefore y=\pm a\sqrt{(1-e^2)}\); ইহা স্পষ্ট যে \(Y\)-অক্ষ উপবৃত্তকে দুইটি বাস্তব বিন্দুতে (যেহেতু \(1>e \)) ছেদ করে।
ধরি,
\(B\) ও \(\acute B\) বিন্দু দুইটি \(C\)-এর বিপরীত দিকে এমনভাবে অবস্থিত যে,
\(CB=C\acute B=a\sqrt{(1-e^2)}\)।
ধরি,
\(CB=C\acute B=b\)
তাহলে, \(b=a\sqrt{(1-e^2)}\)
\(\therefore b^2=a^2(1-e^2) ........(4)\) ➜ উভয় পার্শ্বে বর্গ করে।
\((4)\)-এর সাহায্য নিয়ে \((3)\) হতে পাই,
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই উপবৃত্তের আদর্শ সমীকরণ।
উপবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ
Identifying the standard equation of an ellipse
মূলবিন্দু কেন্দ্রবিশিষ্ট উপবৃত্তের প্রমিত সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এ \(x\) বা \(y\) যুক্ত পদ থাকবে না। শুধু \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ \(\frac{1}{a^2}\) এবং \(y^2\)-এর সহগ \(\frac{1}{b^2}\) অসমান ও অভিন্ন চিহ্নযুক্ত।
উপবৃত্তের সমীকরণ সনাক্তকরণ
Identifying the equation of the ellipse
উপবৃত্তের সমীকরণে \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ এবং \(y^2\)-এর সহগ অসমান ও অভিন্ন চিহ্নযুক্ত। \(x\) ও \(y\) যুক্ত পদ থাকতেও পারে নাও থাকতে পারে।
উপবৃত্তের ক্ষেত্রফল
Area of ellipse
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের ক্ষেত্রফল \(=\pi ab\)
উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর
Equation of the ellipse whose Major axis along \(x\) axis
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (a\gt{b})\)
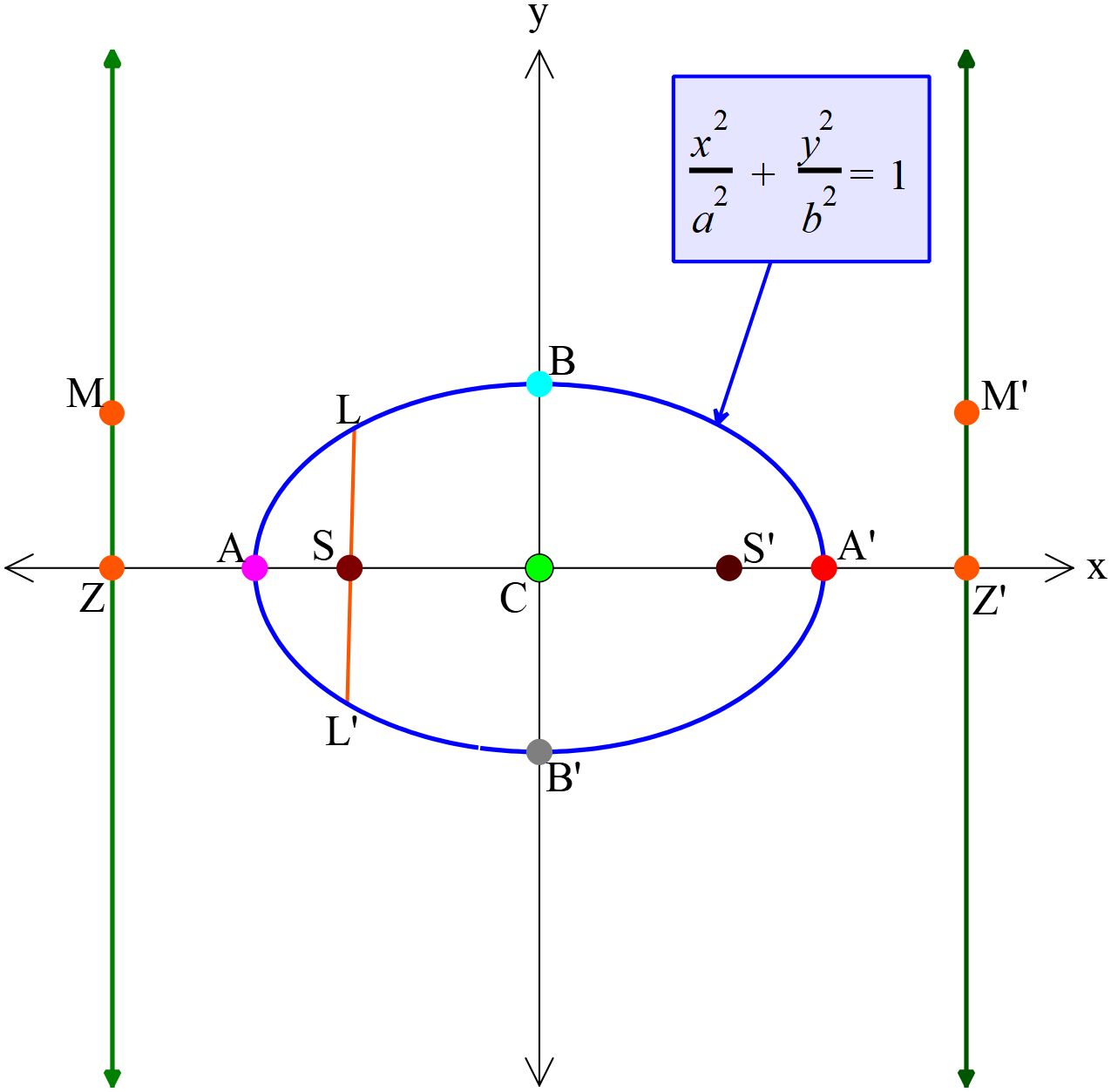
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)
- বৃহদাক্ষের সমীকরণ \(y=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(x=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae, 0)\)
- নিয়ামকরেখার সমীকরণ \(x=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=\pm ae\) অথবা, \(x=\pm\sqrt{a^2-b^2}\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((\pm a, 0)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((\pm \frac{a}{e}, 0)\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2ae|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2a}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(=|\frac{a}{e}-ae|\)
- কেন্দ্র হতে উপকেন্দ্রের দূরত্ব \(=\sqrt{a^2-b^2}\)
প্রমাণঃ
আমরা জানি,
উপবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\therefore b^2=a^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2+y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}+\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শ্বে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
আমরা জানি,
উপবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\therefore b^2=a^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2+y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}+\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শ্বে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর
Equation of the ellipse whose Major axis along \(y\) axis
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (a\lt{b})\)
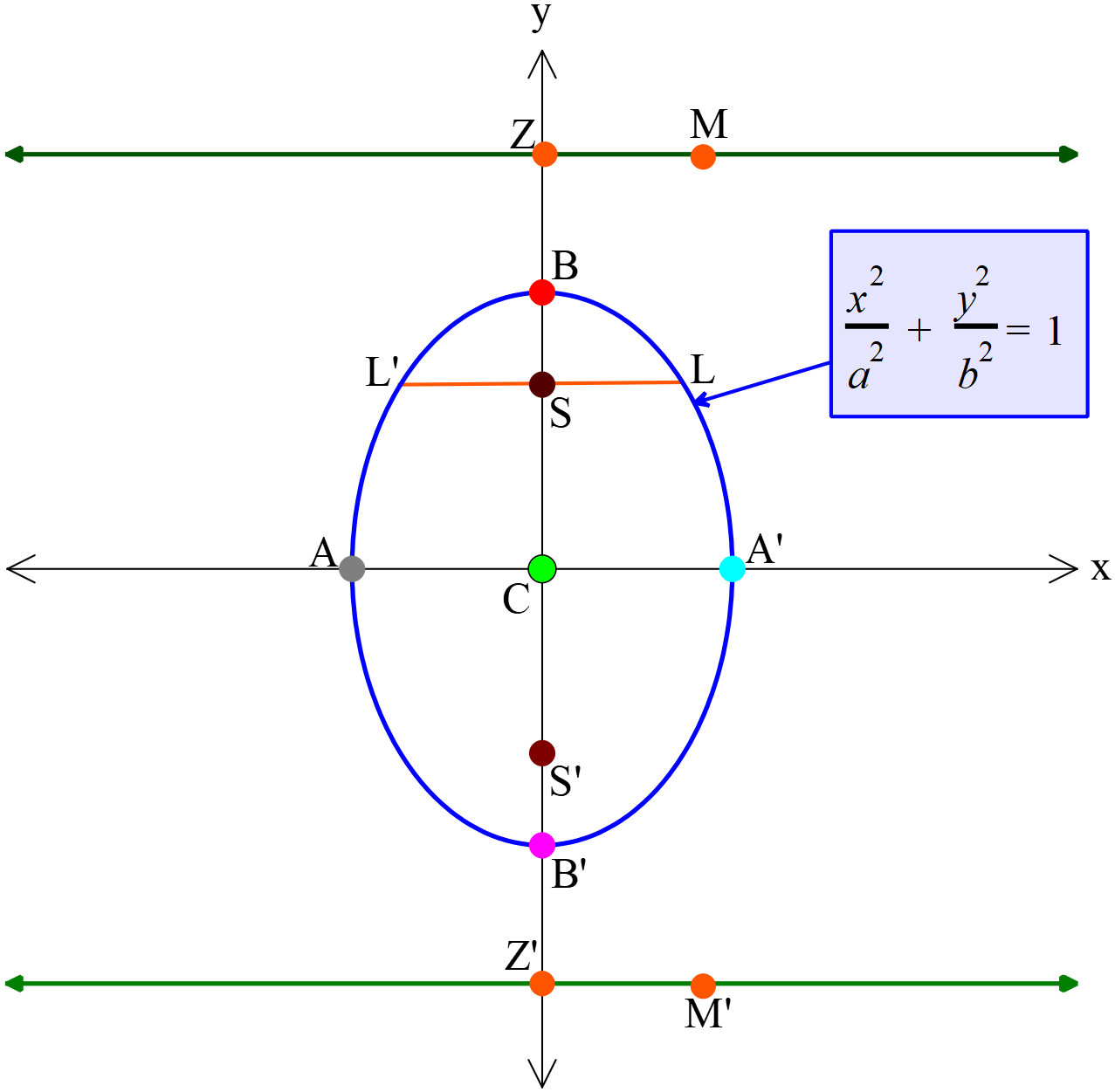
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2b|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2a|\)
- বৃহদাক্ষের সমীকরণ \(x=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(y=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((0, \pm be)\)
- নিয়ামকরেখার সমীকরণ \(y=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=\pm be\) অথবা, \(y=\pm\sqrt{b^2-a^2}\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((0, \pm b)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((0, \pm \frac{b}{e})\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2be|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2b}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(=|\frac{b}{e}-be|\)
- কেন্দ্র হতে উপকেন্দ্রের দূরত্ব \(=\sqrt{b^2-a^2}\)
প্রমাণঃ
আমরা জানি,
উপবৃত্তের উপকেন্দ্র \(S(0, be)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1-\frac{a^2}{b^2}\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow \frac{a^2}{b^2}=1-e^2\)
\(\therefore a^2=b^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2+y^2(1-e^2)=b^2-b^2e^2\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.b^2(1-e^2)=b^2(1-e^2)\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.a^2=a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}.\frac{a^2}{a^2}=\frac{a^2}{a^2}\) ➜ উভয় পার্শ্বে \(a^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
আমরা জানি,
উপবৃত্তের উপকেন্দ্র \(S(0, be)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1-\frac{a^2}{b^2}\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow \frac{a^2}{b^2}=1-e^2\)
\(\therefore a^2=b^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শ্বে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2+y^2(1-e^2)=b^2-b^2e^2\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.b^2(1-e^2)=b^2(1-e^2)\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.a^2=a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}.\frac{a^2}{a^2}=\frac{a^2}{a^2}\) ➜ উভয় পার্শ্বে \(a^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর
Equation of an ellipse with fixed center whose major axis is along the \(x\) axis
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (a\gt{b})\)
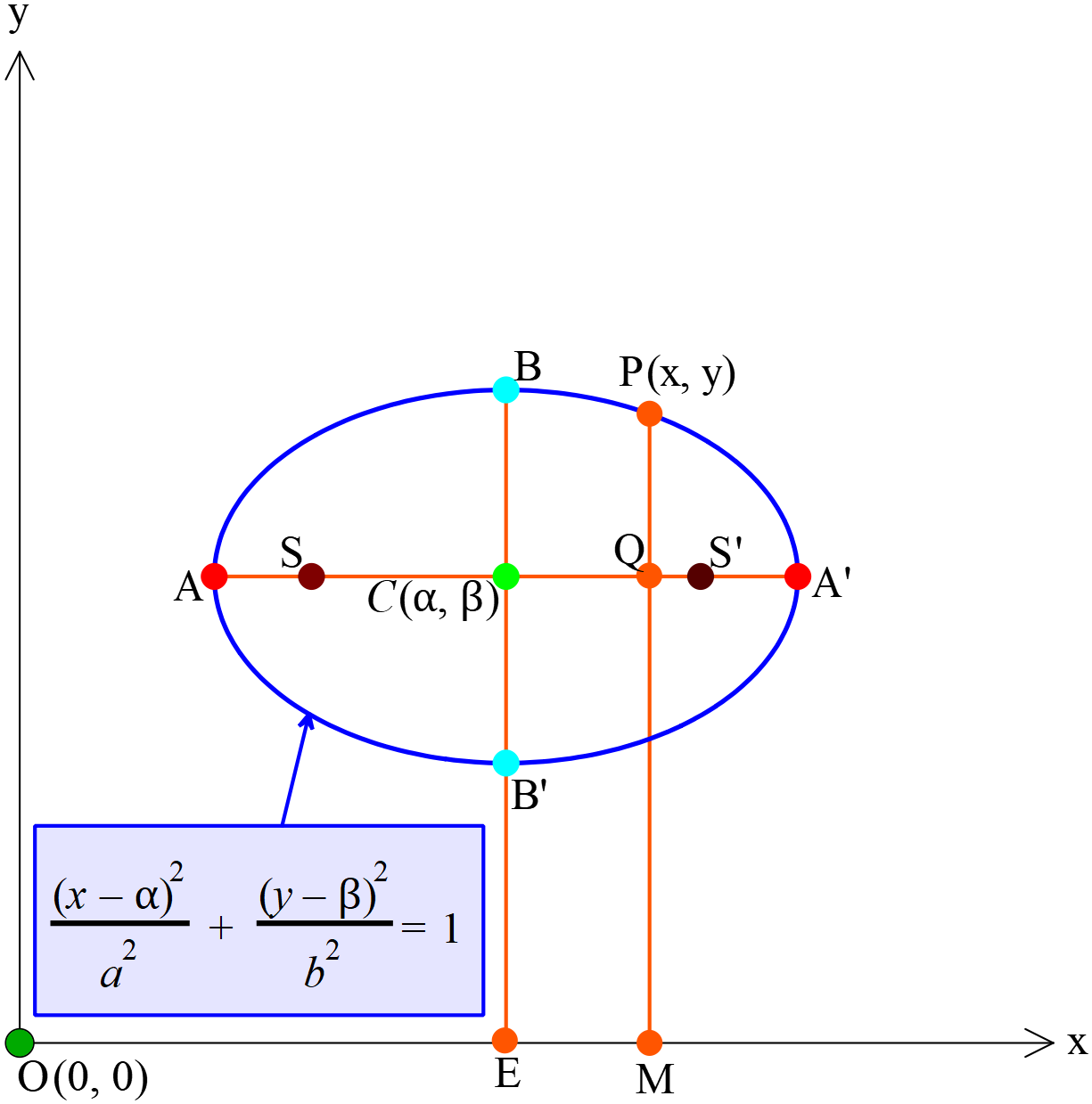
- শীর্ষবিন্দুর স্থানাঙ্ক \((\pm{a}+\alpha, \beta)\)
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)
- বৃহদাক্ষের সমীকরণ \(y-\beta=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(x-\alpha=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae+\alpha, \beta)\)
- নিয়ামকরেখার সমীকরণ \(x-\alpha=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x-\alpha=\pm ae\)
প্রমাণঃ
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
ক্ষুদ্রাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
ক্ষুদ্রাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর
Equation of an ellipse with fixed center whose major axis is along the \(y\) axis
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (a\lt{b})\)
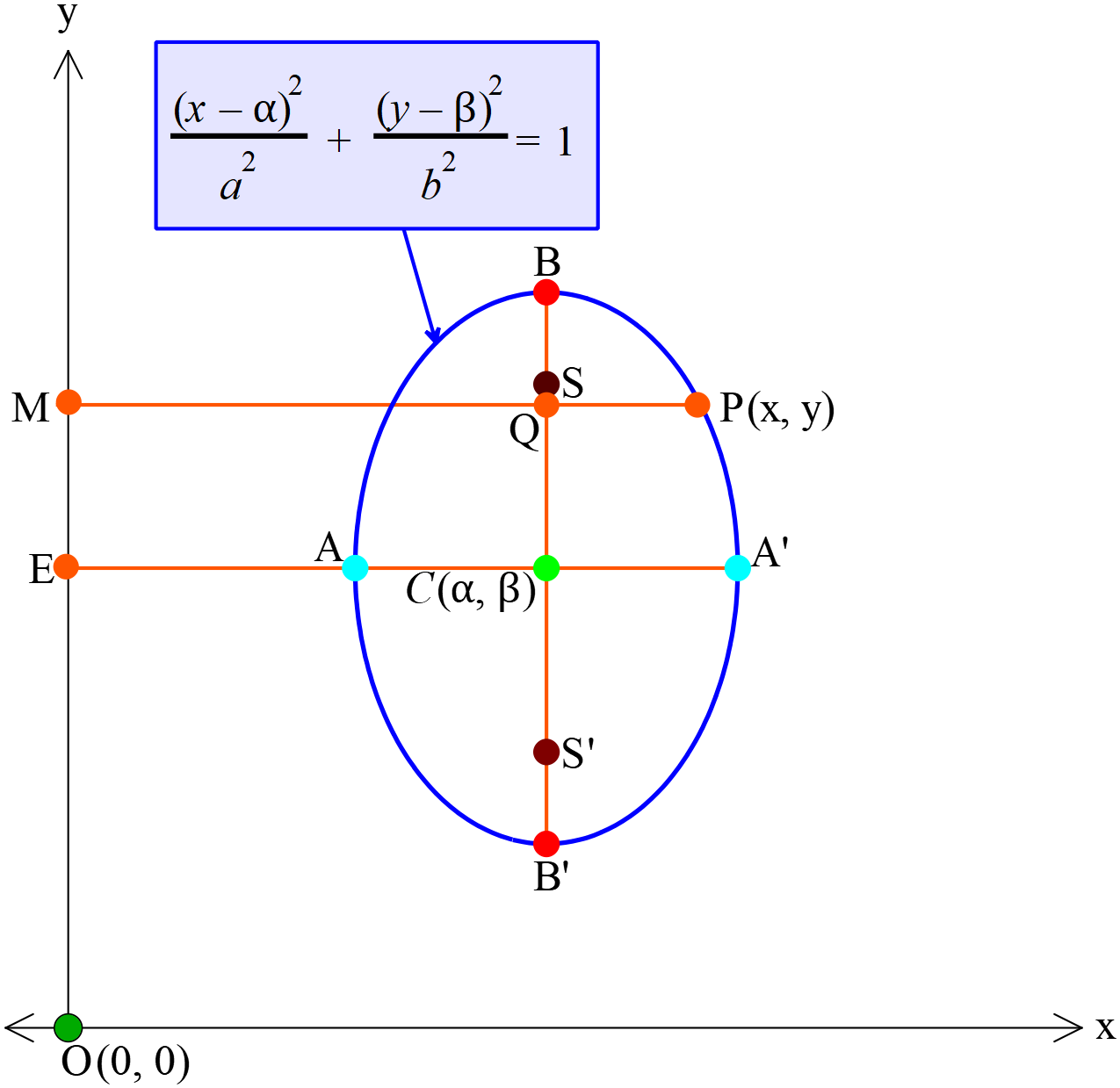
- শীর্ষবিন্দুর স্থানাঙ্ক \((\alpha, \pm b+\beta)\)
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2b|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2a|\)
- বৃহদাক্ষের সমীকরণ \(x-\alpha=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(y-\beta=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\alpha, \pm be+\beta)\)
- নিয়ামকরেখার সমীকরণ \(y-\beta=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y-\beta=\pm be\)
প্রমাণঃ
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
ক্ষুদ্রাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
ক্ষুদ্রাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
\(y=mx+c\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত
The condition of the straight line \(y=mx+c\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(y=mx+c\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(c=\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শকের সমীকরণঃ \(y=mx\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
প্রমাণঃ
মনে করি,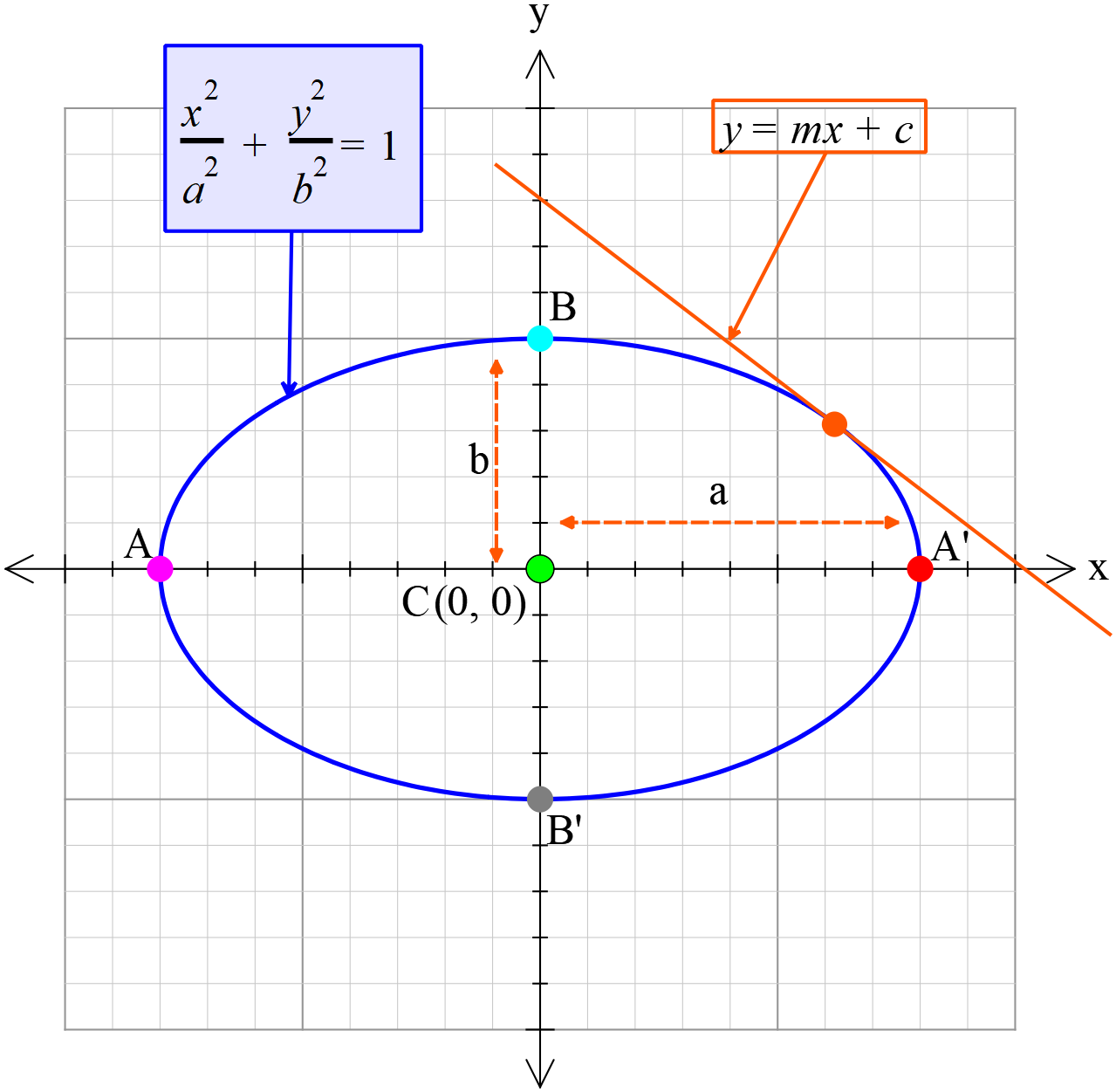
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ...(2)\)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}+\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2+a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শ্বে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2+a^2m^2x^2+2a^2mcx+a^2c^2-a^2b^2=0\)
\(\Rightarrow (a^2m^2+b^2)x^2+2a^2mcx+a^2(c^2-b^2)=0...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
যেমনঃ
\((i)\) \(x_1\) ও \(x_2\) বাস্তব ও অসমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে দুইটি ভিন্ন বিন্দুতে ছেদ করবে।
\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((2a^2mc)^2=4.(a^2m^2+b^2).a^2(c^2-b^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2).a^2(c^2-b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2)(a^2c^2-a^2b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2c^2-a^2b^2)(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^2c^2(a^2m^2+b^2)-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^4c^2m^2+a^2b^2c^2-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2-a^4m^2c^2-a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow -a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow c^2=(a^2m^2+b^2)\) ➜ উভয় পার্শ্বে \(-a^2b^2\) ভাগ করে।
\(\therefore c=\pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{-2a^2mc}{2(a^2m^2+b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{-a^2mc}{a^2m^2+b^2}\)
\(\Rightarrow x=\frac{-a^2m\times \pm \sqrt{(a^2m^2+b^2)}}{a^2m^2+b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2+b^2)}}{\sqrt{(a^2m^2+b^2)}\times \sqrt{(a^2m^2+b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=-\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2-b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2+b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ...(2)\)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}+\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2+a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শ্বে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2+a^2m^2x^2+2a^2mcx+a^2c^2-a^2b^2=0\)
\(\Rightarrow (a^2m^2+b^2)x^2+2a^2mcx+a^2(c^2-b^2)=0...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
যেমনঃ
\((i)\) \(x_1\) ও \(x_2\) বাস্তব ও অসমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে দুইটি ভিন্ন বিন্দুতে ছেদ করবে।
\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((2a^2mc)^2=4.(a^2m^2+b^2).a^2(c^2-b^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2).a^2(c^2-b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2)(a^2c^2-a^2b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2c^2-a^2b^2)(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^2c^2(a^2m^2+b^2)-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^4c^2m^2+a^2b^2c^2-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2-a^4m^2c^2-a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow -a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow c^2=(a^2m^2+b^2)\) ➜ উভয় পার্শ্বে \(-a^2b^2\) ভাগ করে।
\(\therefore c=\pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{-2a^2mc}{2(a^2m^2+b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{-a^2mc}{a^2m^2+b^2}\)
\(\Rightarrow x=\frac{-a^2m\times \pm \sqrt{(a^2m^2+b^2)}}{a^2m^2+b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2+b^2)}}{\sqrt{(a^2m^2+b^2)}\times \sqrt{(a^2m^2+b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=-\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2-b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2+b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
\(x\cos\alpha + y\sin\alpha=p\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত
The condition of the straight line \(x\cos\alpha + y\sin\alpha=p\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(x\cos\alpha + y\sin\alpha=p\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(p^2=a^2\cos^2\alpha+b^2\sin^2\alpha\)
স্পর্শকের সমীকরণঃ \(x\cos\alpha + y\sin\alpha \pm \sqrt{(a^2\cos^2\alpha+b^2\sin^2\alpha)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a^2\cos\alpha}{p}, \frac{b^2\sin\alpha}{p}\right)\)
\(lx+my+n=0\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত
The condition of the straight line \(lx+my+n=0\) being tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(lx+my+n=0\) সরলরেখা \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(a^2l^2+b^2m^2=n^2\)
স্পর্শকের সমীকরণঃ \(lx+my \pm \sqrt{(a^2l^2+b^2m^2)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{-a^2l}{n}, \frac{-b^2m}{n}\right)\)
উপবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান
The relative position of a point with respect to the ellipse
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের উপরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}=0\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের ভিতরে অবস্থান করার শর্তঃ \(0>\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের বাহিরে অবস্থান করার শর্তঃ\(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2} > 0\)
উপবৃত্তের উপরিস্থিত নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকর
Equation of the tangent at a given point on the ellipse
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\((1)\) নং উপবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{xx_1}{a^2}+\frac{yy_1}{b^2}=1\)
উপবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা
Focus and directrix of Ellipse
একটি উপবৃত্তের দুইটি উপকেন্দ্র ও নিয়ামকরেখা আছে। যেহেতু, উপবৃত্তটি \(y\) অক্ষ বরাবর প্রতিসম তাই তাকে \(B\acute B\) বরাবর ভাঁজ করা হলে উপবৃত্তের ডান ও বাম পক্ষ দুইটি পরস্পরের সাথে সমাপতিত হয়। এখন \(x\) অক্ষের উপর \(\acute S\) ও \(\acute Z\) দুইটি বিন্দু এমনভাবে নেওয়া হয়, যেন \(C\acute S=CS=ae \) এবং \(C\acute Z=CZ=\frac{a}{e}\) হয়। \(Z\acute Z\)-এর উপর \(\acute M\acute Z\) লম্ব আঁকি। তাহলে প্রতিসাম্য অনুযায়ী, এটি স্পষ্ট যে, \(\acute S\)-কে উপকেন্দ্র এবং \(\acute M\acute Z\)-কে নিয়ামকরেখা ধরে আমরা একই উপবৃত্ত পাই। অতএব, উপবৃত্তের দুইটি উপকেন্দ্র এবং দুইটি নিয়ামকরেখা আছে।
উপবৃত্তের বৃহদাক্ষ ও ক্ষুদ্রাক্ষের
Major and Minor axis of Ellipse
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1)\)
\(a\gt{b}\) ধরে \(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\) সুতরাং উপবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) বৃহদাক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow 0+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=b^2\)
\(\therefore y=\pm b\)
সুতরাং উপবৃত্ত \(Y\)-অক্ষকে \(B(0, b)\) এবং \(\acute B(0, -b)\) বিন্দুতে ছেদ করে।
\(B\acute B\) ক্ষুদ্রাক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)।
\(a\gt{b}\) ধরে \(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\) সুতরাং উপবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) বৃহদাক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow 0+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=b^2\)
\(\therefore y=\pm b\)
সুতরাং উপবৃত্ত \(Y\)-অক্ষকে \(B(0, b)\) এবং \(\acute B(0, -b)\) বিন্দুতে ছেদ করে।
\(B\acute B\) ক্ষুদ্রাক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)।
উপবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা
Eccentricity from the equation of ellipse
আমরা জানি,
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\)
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1-\frac{b^2}{a^2}}\)
যেহেতু, উপবৃত্তের \(e\)-এর মান \(1 > e > 0\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
উপবৃত্তের বৃহদাক্ষ হতে \(a\)-এর মান এবং ক্ষুদ্রাক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\)
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1-\frac{b^2}{a^2}}\)
যেহেতু, উপবৃত্তের \(e\)-এর মান \(1 > e > 0\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
উপবৃত্তের বৃহদাক্ষ হতে \(a\)-এর মান এবং ক্ষুদ্রাক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।
উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ
The co-ordinates of focus and the equation of directrix from the equation of ellipse
মনে করি,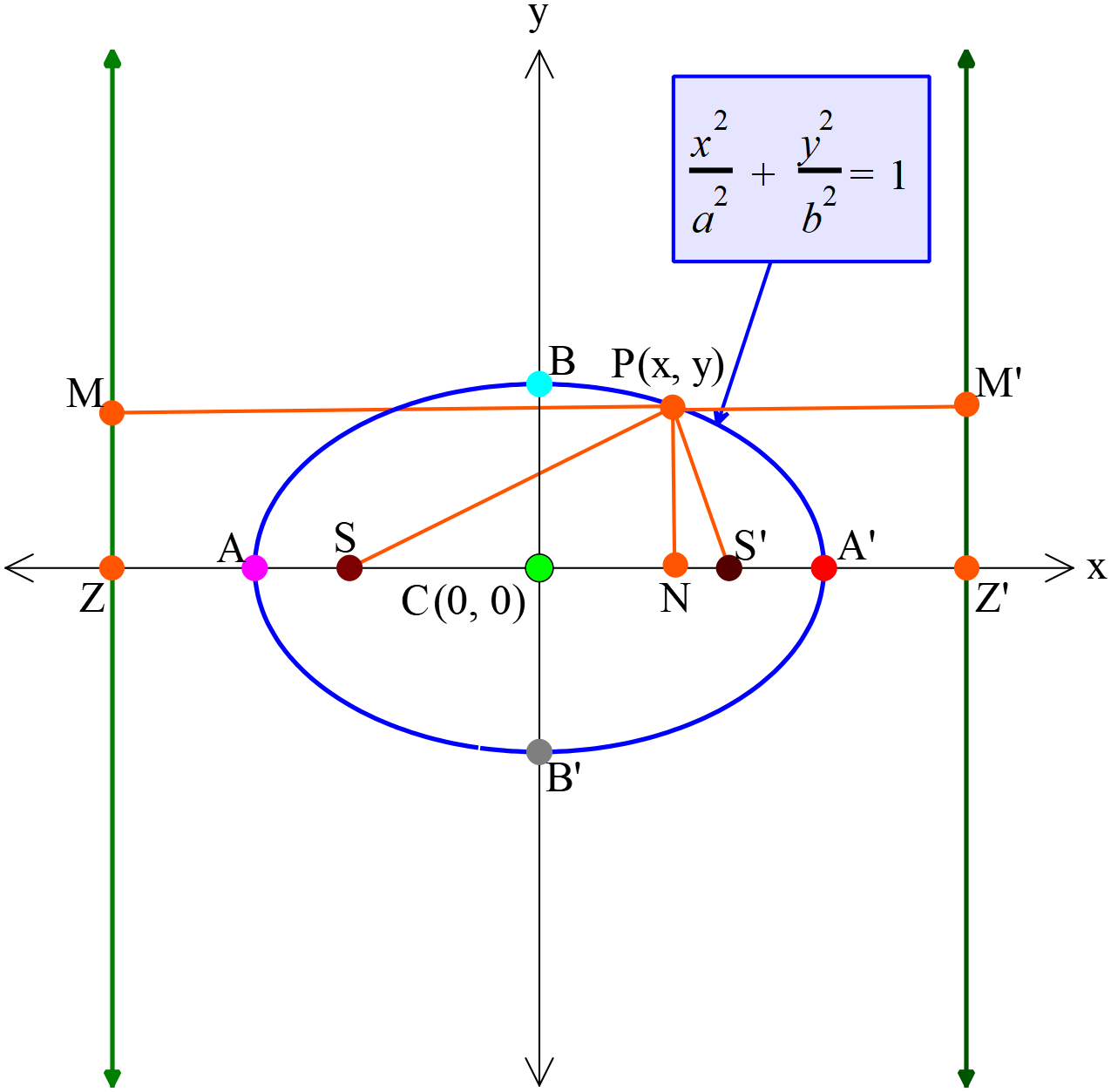
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\)অক্ষ এবং \(CY\)-কে \(y\)অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\)অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\)অক্ষ এবং \(CY\)-কে \(y\)অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\)অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)
উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য
From the equation of an ellipse Latus rectum and it's length
উপবৃত্তের যে কোনো উপকেন্দ্রের মধ্য দিয়ে অঙ্কিত বৃহদাক্ষের উপর লম্ব রেখার উপবৃত্তের অন্তর্গত অংশই উপকেন্দ্রিক লম্ব। যদি \(L\acute L\) উপকেন্দ্রিক লম্ব হয়, তবে \(SL=S\acute L\) এবং \(\acute L\)-এর স্থানাঙ্ক \((-ae, SL)\) ।
\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{SL^2}{b^2}=1-e^2 \)
\(\Rightarrow SL^2=b^2(1-e^2) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because 1-e^2=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)
\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{SL^2}{b^2}=1-e^2 \)
\(\Rightarrow SL^2=b^2(1-e^2) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because 1-e^2=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)
উপবৃত্তের উপরিস্থিত কোনো বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান
Sum of the two epicentral distance of a point on the ellipse is equal to the length of Major axis
ধরি,
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের উপরিস্থিত কোনো বিন্দু \(P(x, y)\)।
উপবৃত্তের উপকেন্দ্র দুইটি \(S\) ও \(\acute S\) এবং নিয়ামক রেখা দুইটি যথাক্রমে \(MZ\) ও \(\acute M\acute Z\) ।
\(SP\) এবং \(\acute SP\) যোগ করি এবং নিয়ামক রেখা দইটির উপর \(MP\acute M\) লম্ব আঁকি।
এখন,
উপবৃত্তের সংজ্ঞানুসারে,
\(SP=e.PM .......(1)\)
এবং \(\acute SP=e.P\acute M .......(2)\)
\((1)\) ও \((2)\) যোগ করে,
\(SP+\acute SP=e.PM+e.P\acute M\)
\(\Rightarrow SP+\acute SP=e(PM+P\acute M)\)
\(\Rightarrow SP+\acute SP=e\{(CZ+CN)+(C\acute Z-CN)\}\) ➜ \(\because PM=CZ+CN; P\acute M=C\acute Z-CN\)
\(\Rightarrow SP+\acute SP=e\{CZ+CN+C\acute Z-CN\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+C\acute Z\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+CZ\}\) ➜ \(\because CZ=C\acute Z\)
\(\Rightarrow SP+\acute SP=e.2CZ\)
\(\Rightarrow SP+\acute SP=2.e.CZ\)
\(\Rightarrow SP+\acute SP=2.CA\) ➜ \(\because e.CZ=CA\)
\(\Rightarrow SP+\acute SP=A\acute A\) ➜ \(\because 2.CA=A\acute A\)
\(\therefore SP+\acute SP=2a\) ➜ \(\because A\acute A=2a\)
\(\therefore \) উপবৃত্তের উপরিস্থিত \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান। ইহা অতি গুরুত্বপূর্ণ।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের উপরিস্থিত কোনো বিন্দু \(P(x, y)\)।
উপবৃত্তের উপকেন্দ্র দুইটি \(S\) ও \(\acute S\) এবং নিয়ামক রেখা দুইটি যথাক্রমে \(MZ\) ও \(\acute M\acute Z\) ।
\(SP\) এবং \(\acute SP\) যোগ করি এবং নিয়ামক রেখা দইটির উপর \(MP\acute M\) লম্ব আঁকি।
এখন,
উপবৃত্তের সংজ্ঞানুসারে,
\(SP=e.PM .......(1)\)
এবং \(\acute SP=e.P\acute M .......(2)\)
\((1)\) ও \((2)\) যোগ করে,
\(SP+\acute SP=e.PM+e.P\acute M\)
\(\Rightarrow SP+\acute SP=e(PM+P\acute M)\)
\(\Rightarrow SP+\acute SP=e\{(CZ+CN)+(C\acute Z-CN)\}\) ➜ \(\because PM=CZ+CN; P\acute M=C\acute Z-CN\)
\(\Rightarrow SP+\acute SP=e\{CZ+CN+C\acute Z-CN\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+C\acute Z\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+CZ\}\) ➜ \(\because CZ=C\acute Z\)
\(\Rightarrow SP+\acute SP=e.2CZ\)
\(\Rightarrow SP+\acute SP=2.e.CZ\)
\(\Rightarrow SP+\acute SP=2.CA\) ➜ \(\because e.CZ=CA\)
\(\Rightarrow SP+\acute SP=A\acute A\) ➜ \(\because 2.CA=A\acute A\)
\(\therefore SP+\acute SP=2a\) ➜ \(\because A\acute A=2a\)
\(\therefore \) উপবৃত্তের উপরিস্থিত \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান। ইহা অতি গুরুত্বপূর্ণ।
কোনো সমতলে, কোনো সেটের বিন্দুসমুহ যদি এমনভাবে অবস্থিত হয় যে, ঐ সমতলে অবস্থিত দুইটি নির্দিষ্ট বিন্দু হতে এর দূরত্ব দুইটির সমষ্টি সর্বদা স্থীর হয় তাহলে উক্ত বিন্দু সেটের সঞ্চারপথ উপবৃত্ত হবে।
উপবৃত্তের বৃহৎ অক্ষ এর বৃহত্তম জ্যা।
উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক যখন \((a\gt{b})\)
Parametric coordinates of a given point on the ellipse when \((a\gt{b})\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\gt{b})\) উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক।
ধরি,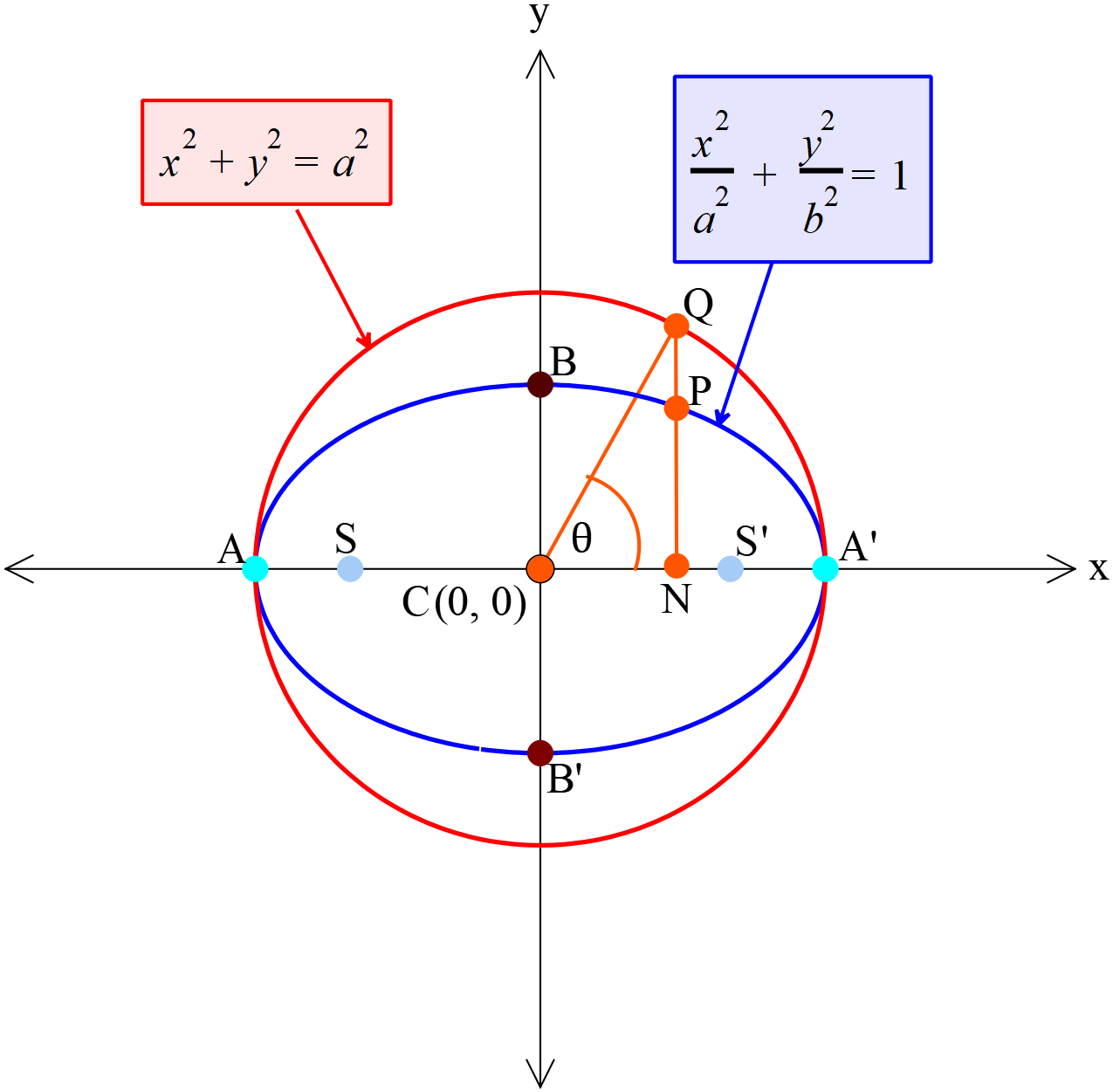
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\gt{b}) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos\theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos\theta\)
\(\therefore x=a\cos\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\cos\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\cos\theta)^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\cos^2\theta}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \cos^2\theta+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1-\cos^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\sin^2\theta\)
\(\Rightarrow y^2=b^2\sin^2\theta\)
\(\therefore y=b\sin\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\cos\theta=\frac{x}{a} ........(5)\)
\(\sin\theta=\frac{y}{b} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((6)\)-কে \((5)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\gt{b}) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\gt{b}) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos\theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos\theta\)
\(\therefore x=a\cos\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\cos\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\cos\theta)^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\cos^2\theta}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \cos^2\theta+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1-\cos^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\sin^2\theta\)
\(\Rightarrow y^2=b^2\sin^2\theta\)
\(\therefore y=b\sin\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\cos\theta=\frac{x}{a} ........(5)\)
\(\sin\theta=\frac{y}{b} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((6)\)-কে \((5)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\gt{b}) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক যখন \((a\lt{b})\)
Parametric coordinates of a given point on the ellipse when \((a\lt{b})\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\lt{b})\) উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুর পরামিতিক স্থানাঙ্ক।
ধরি,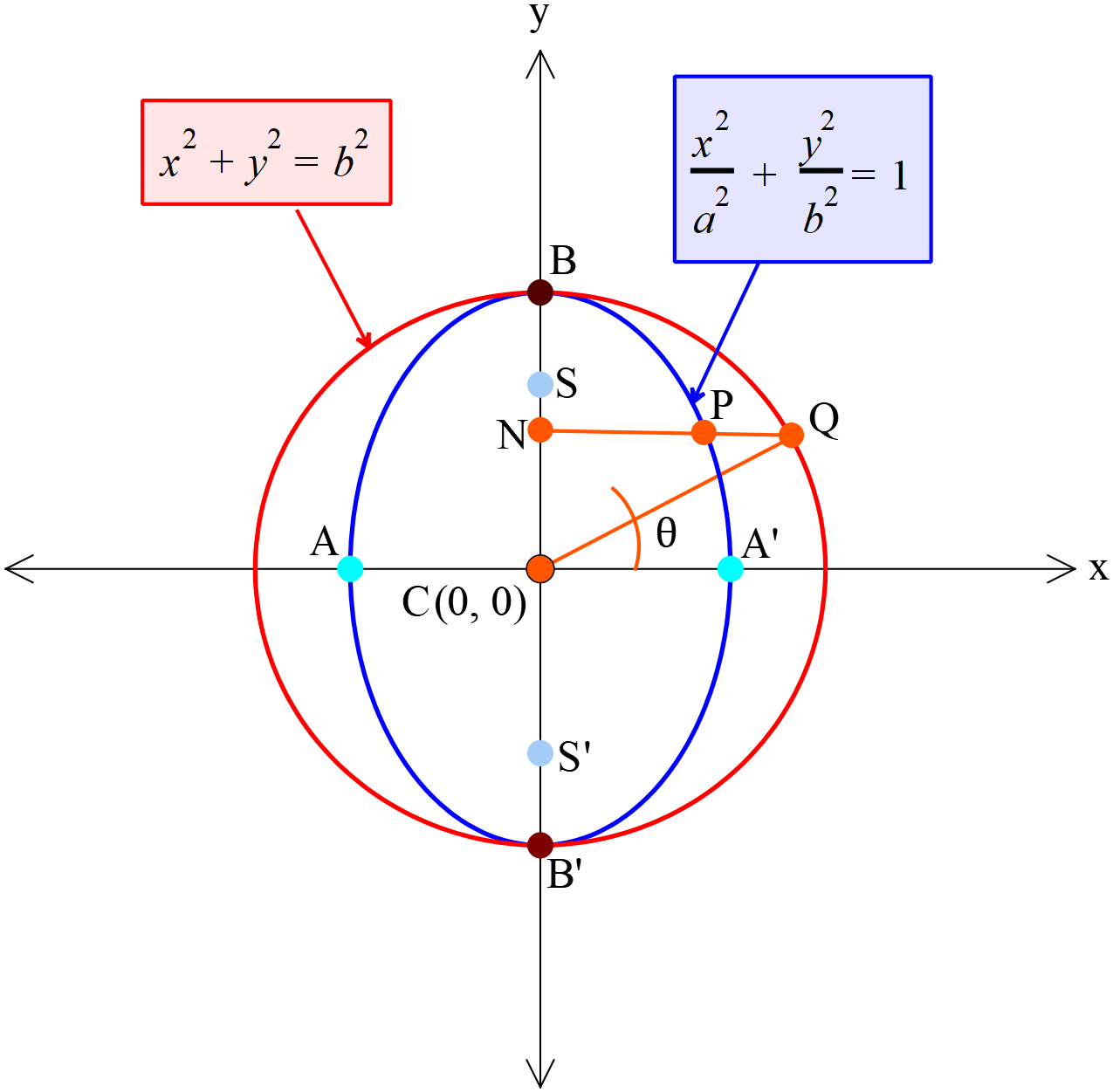
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\lt{b}) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=b^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QC\acute A=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(\therefore \angle QCN=90^{o}-\theta\)
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=y\) এবং \(PN=x\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos(90^{o}-\theta)=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos(90^{o}-\theta)\)
\(\therefore y=b\sin\theta ........(3)\) ➜ \(\because CQ=b=\)বৃত্তের ব্যাসার্ধ।
\(y=b\sin\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{x^2}{a^2}+\frac{(b\sin\theta)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{b^2\sin^2\theta}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\sin^2\theta=1\)
\(\Rightarrow \frac{x^2}{a^2}=1-\sin^2\theta\)
\(\Rightarrow \frac{x^2}{a^2}=\cos^2\theta\)
\(\Rightarrow x^2=a^2\cos^2\theta\)
\(\therefore x=a\cos\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\sin\theta=\frac{y}{b} ........(5)\)
\(\cos\theta=\frac{x}{a} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((5)\)-কে \((6)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\lt{b}) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\lt{b}) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=b^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QC\acute A=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(\therefore \angle QCN=90^{o}-\theta\)
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=y\) এবং \(PN=x\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos(90^{o}-\theta)=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos(90^{o}-\theta)\)
\(\therefore y=b\sin\theta ........(3)\) ➜ \(\because CQ=b=\)বৃত্তের ব্যাসার্ধ।
\(y=b\sin\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{x^2}{a^2}+\frac{(b\sin\theta)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{b^2\sin^2\theta}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\sin^2\theta=1\)
\(\Rightarrow \frac{x^2}{a^2}=1-\sin^2\theta\)
\(\Rightarrow \frac{x^2}{a^2}=\cos^2\theta\)
\(\Rightarrow x^2=a^2\cos^2\theta\)
\(\therefore x=a\cos\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\sin\theta=\frac{y}{b} ........(5)\)
\(\cos\theta=\frac{x}{a} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((5)\)-কে \((6)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a\lt{b}) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
বিঃ দ্রঃ ইহা স্পষ্ট যে উপবৃত্তের আকার যাই হউকনা কেন ইহার উপরোস্থ যে কোনো বিন্দুর পরামিতিক স্থানাঙ্ক হবে \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\). এবং উপবৃত্তের পরামিতিক সমীকরণ হবে
\(x=a\cos\theta\), \(y=b\sin\theta\).
\(x=a\cos\theta\), \(y=b\sin\theta\).
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর লেখচিত্র
Graph of equation of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)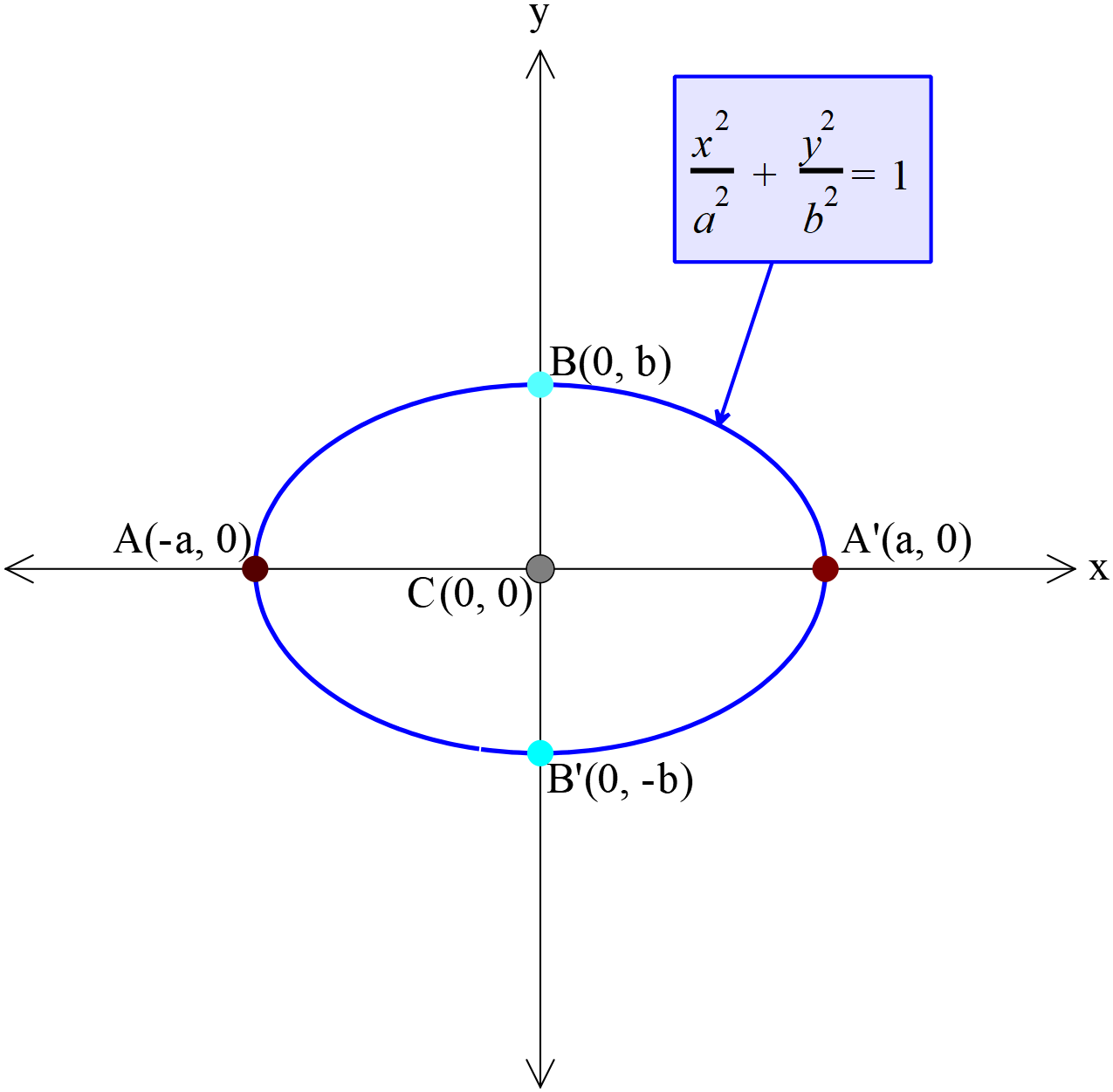
\(\Rightarrow \frac{y^2}{b^2}=1-\frac{x^2}{a^2}\)
\(\Rightarrow \frac{y^2}{b^2}=\frac{a^2-x^2}{a^2}\)
\(\Rightarrow y^2=\frac{b^2(a^2-x^2)}{a^2}\)
\(\Rightarrow y=\pm \sqrt{\frac{b^2(a^2-x^2)}{a^2}}\)
\(\therefore y=\pm b\sqrt{\frac{(a^2-x^2)}{a^2}}\)
\(\therefore a>x\)-এর যে কোনো মানের জন্য \(y\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে, উপবৃত্তটি \(X\)-অক্ষ ( বৃহৎ অক্ষ ) বরাবর প্রতিসম।
আবার,
\(x\)-এর সর্বোচ্চ মান \(a\) এবং সর্বনিম্ন মান \(-a\) কারণ, যদি \(x > a\) বা \(-a>x\) হয়, তবে,
\(\frac{a^2-x^2}{a^2}\) ঋনাত্মক হয় এবং \(y\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(x\)-অক্ষের উপর \(A\) ও \(\acute A\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
উপবৃত্তের সমীকরণটিকে নিম্নোক্তভাবেও লেখা যায়,\(\therefore x=\pm a\sqrt{\frac{(b^2-y^2)}{b^2}}\)
\(\therefore b > y\)-এর যে কোনো মানের জন্য \(x\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে, উপবৃত্তটি \(Y\)-অক্ষ (ক্ষুদ্র অক্ষ ) বরাবর প্রতিসম।
\(y\)-এর সর্বোচ্চ মান \(b\) এবং সর্বনিম্ন মান \(-b\) কারণ, যদি \(y > b\) বা \(-b > y\) হয়, তবে,
\(\frac{b^2-y^2}{b^2}\) ঋনাত্মক হয় এবং \(x\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(y\)-অক্ষের উপর \(B\) ও \(\acute B\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
অতএব , উপবৃত্ত একটি সীমাবদ্ধ বক্ররেখা, যা, পুরাপুরি \(x=\pm a, y=\pm b\) সরলরেখা চতুষ্টয় দ্বারা সীমিত আয়তের মধ্যে অবস্থিত।
\(\Rightarrow \frac{y^2}{b^2}=1-\frac{x^2}{a^2}\)
\(\Rightarrow \frac{y^2}{b^2}=\frac{a^2-x^2}{a^2}\)
\(\Rightarrow y^2=\frac{b^2(a^2-x^2)}{a^2}\)
\(\Rightarrow y=\pm \sqrt{\frac{b^2(a^2-x^2)}{a^2}}\)
\(\therefore y=\pm b\sqrt{\frac{(a^2-x^2)}{a^2}}\)
\(\therefore a>x\)-এর যে কোনো মানের জন্য \(y\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে, উপবৃত্তটি \(X\)-অক্ষ ( বৃহৎ অক্ষ ) বরাবর প্রতিসম।
আবার,
\(x\)-এর সর্বোচ্চ মান \(a\) এবং সর্বনিম্ন মান \(-a\) কারণ, যদি \(x > a\) বা \(-a>x\) হয়, তবে,
\(\frac{a^2-x^2}{a^2}\) ঋনাত্মক হয় এবং \(y\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(x\)-অক্ষের উপর \(A\) ও \(\acute A\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
উপবৃত্তের সমীকরণটিকে নিম্নোক্তভাবেও লেখা যায়,\(\therefore x=\pm a\sqrt{\frac{(b^2-y^2)}{b^2}}\)
\(\therefore b > y\)-এর যে কোনো মানের জন্য \(x\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে, উপবৃত্তটি \(Y\)-অক্ষ (ক্ষুদ্র অক্ষ ) বরাবর প্রতিসম।
\(y\)-এর সর্বোচ্চ মান \(b\) এবং সর্বনিম্ন মান \(-b\) কারণ, যদি \(y > b\) বা \(-b > y\) হয়, তবে,
\(\frac{b^2-y^2}{b^2}\) ঋনাত্মক হয় এবং \(x\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(y\)-অক্ষের উপর \(B\) ও \(\acute B\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
অতএব , উপবৃত্ত একটি সীমাবদ্ধ বক্ররেখা, যা, পুরাপুরি \(x=\pm a, y=\pm b\) সরলরেখা চতুষ্টয় দ্বারা সীমিত আয়তের মধ্যে অবস্থিত।
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004