এ অধ্যায়ের পাঠ্যসূচী
- উপ-গুণিতক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of sub-multiple angles)
- \(\sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
- \(1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
- \(1-\sin{A}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
- \(\sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
- \(\cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
- \(\cos{A}=2\cos^2{\frac{A}{2}}-1\)
- \(\cos{A}=1-2\sin^2{\frac{A}{2}}\)
- \(1+\cos{A}=2\cos^2{\frac{A}{2}}\)
- \(1-\cos{A}=2\sin^2{\frac{A}{2}}\)
- \(\cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
- \(\frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)
- \(\tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
- \(\cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
- \(\sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
- \(\cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
- \(\tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
- \(\cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{\frac{A}{3}}}{3\cot^2{\frac{A}{3}}-1}\)
- \(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
- \(15^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(15^{o}\))
- \(18^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(18^{o}\))
- \(36^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(36^{o}\))
- \(54^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(54^{o}\))
- \(72^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(72^{o}\))
- \(75^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of the angle \(75^{o}\))
- অধ্যায় \(vii.E\)-এর উদাহরণসমুহ
- অধ্যায় \(vii.E\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(vii.E\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vii.E\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vii.E\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
উপ-গুণিতক কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of sub-multiple angles
একটি কোণকে কোনো পূর্ণসংখ্যা দ্বারা ভাগ করলে উক্ত কোণের উপ-গুণিতক কোণ পাওয়া যায়।
যেমনঃ \(A\) কোণের উপ-গুণিতক কোণগুলি \(\frac{A}{2}, \ \frac{A}{3}, \ \frac{A}{4} .........\frac{A}{n}\) ইত্যাদি।
যেমনঃ \(A\) কোণের উপ-গুণিতক কোণগুলি \(\frac{A}{2}, \ \frac{A}{3}, \ \frac{A}{4} .........\frac{A}{n}\) ইত্যাদি।
\(\sin{A}\) কে \(\sin{\frac{A}{2}}\) এবং \(\cos{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\sin{A}\) in terms of \(\sin{\frac{A}{2}}\) and \(\cos{\frac{A}{2}}\)
\(\sin{A}\) কে \(\sin{\frac{A}{2}}\) এবং \(\cos{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(1-\sin{2}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(1-\sin{2}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
প্রমাণঃ
আমরা জানি,
\(\sin{2A}=2\sin{A}\cos{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\sin{\left(2\times\frac{A}{2}\right)}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\therefore \sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
আবার,
\(1+\sin{2A}=(\sin{A}+\cos{A})^2 ........(2)\)
\((2)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1+\sin{\left(2\times\frac{A}{2}\right)}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(\therefore 1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
আবার,
\(1-\sin{2A}=(\sin{A}-\cos{A})^2 ........(3)\)
\((3)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1-\sin{\left(2\times\frac{A}{2}\right)}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(\therefore 1-\sin{A}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(1-\sin{A}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
আমরা জানি,
\(\sin{2A}=2\sin{A}\cos{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\sin{\left(2\times\frac{A}{2}\right)}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\therefore \sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
আবার,
\(1+\sin{2A}=(\sin{A}+\cos{A})^2 ........(2)\)
\((2)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1+\sin{\left(2\times\frac{A}{2}\right)}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(\therefore 1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
\(1+\sin{A}=(\sin{\frac{A}{2}}+\cos{\frac{A}{2}})^2\)
আবার,
\(1-\sin{2A}=(\sin{A}-\cos{A})^2 ........(3)\)
\((3)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1-\sin{\left(2\times\frac{A}{2}\right)}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(\therefore 1-\sin{A}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(1-\sin{A}=(\sin{\frac{A}{2}}-\cos{\frac{A}{2}})^2\)
\(\sin{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\sin{A}\) in terms of \(\tan{\frac{A}{2}}\)
\(\sin{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
প্রমাণঃ
আমরা জানি,
\(\sin{2A}=\frac{2\tan{A}}{1+\tan^2{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\sin{\left(2\times\frac{A}{2}\right)}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\therefore \sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
আমরা জানি,
\(\sin{2A}=\frac{2\tan{A}}{1+\tan^2{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\sin{\left(2\times\frac{A}{2}\right)}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\therefore \sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\sin{A}=\frac{2\tan{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\cos{A}\) কে \(\sin{\frac{A}{2}}\) এবং \(\cos{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\cos{A}\) in terms of \(\sin{\frac{A}{2}}\) and \(\cos{\frac{A}{2}}\)
\(\cos{A}\) কে \(\sin{\frac{A}{2}}\) এবং \(\cos{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
\(\cos{A}=2\cos^2{\frac{A}{2}}-1\)
\(\cos{A}=1-2\sin^2{\frac{A}{2}}\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}}\)
\(1-\cos{A}=2\sin^2{\frac{A}{2}}\)
\(\cos{A}=2\cos^2{\frac{A}{2}}-1\)
\(\cos{A}=1-2\sin^2{\frac{A}{2}}\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}}\)
\(1-\cos{A}=2\sin^2{\frac{A}{2}}\)
প্রমাণঃ
আমরা জানি,
\(\cos{2A}=\cos^2{A}-\sin^2{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
\(\therefore \cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
\(\cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
আবার,
\(\cos{2A}=2\cos^2{A}-1 ........(2)\)
\((2)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=2\cos^2{\frac{A}{2}}-1\)
\(\therefore \cos{A}=2\cos^2{\frac{A}{2}}-1\)
\(\cos{A}=2\cos^2{\frac{A}{2}}-1\)
আবার,
\(\cos{2A}=1-2\sin^2{A} ........(3)\)
\((3)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=1-2\sin^2{\frac{A}{2}}\)
\(\therefore \cos{A}=1-2\sin^2{\frac{A}{2}}\)
\(\cos{\left(2\times\frac{A}{2}\right)}=1-2\sin^2{\frac{A}{2}}\)
আবার,
\(1+\cos{2A}=2\cos^2{A} ........(4)\)
\((4)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1+\cos{\left(2\times\frac{A}{2}\right)}=2\cos^2{\frac{A}{2}}\)
\(\therefore 1+\cos{A}=2\cos^2{\frac{A}{2}}\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}}\)
আবার,
\(1-\cos{2A}=2\sin^2{A} ........(5)\)
\((5)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1-\cos{\left(2\times\frac{A}{2}\right)}=2\sin^2{\frac{A}{2}}\)
\(\therefore 1-\cos{A}=2\sin^2{\frac{A}{2}}\)
\(1-\cos{A}=2\sin^2{\frac{A}{2}}\)
আমরা জানি,
\(\cos{2A}=\cos^2{A}-\sin^2{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
\(\therefore \cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
\(\cos{A}=\cos^2{\frac{A}{2}}-\sin^2{\frac{A}{2}}\)
আবার,
\(\cos{2A}=2\cos^2{A}-1 ........(2)\)
\((2)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=2\cos^2{\frac{A}{2}}-1\)
\(\therefore \cos{A}=2\cos^2{\frac{A}{2}}-1\)
\(\cos{A}=2\cos^2{\frac{A}{2}}-1\)
আবার,
\(\cos{2A}=1-2\sin^2{A} ........(3)\)
\((3)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=1-2\sin^2{\frac{A}{2}}\)
\(\therefore \cos{A}=1-2\sin^2{\frac{A}{2}}\)
\(\cos{\left(2\times\frac{A}{2}\right)}=1-2\sin^2{\frac{A}{2}}\)
আবার,
\(1+\cos{2A}=2\cos^2{A} ........(4)\)
\((4)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1+\cos{\left(2\times\frac{A}{2}\right)}=2\cos^2{\frac{A}{2}}\)
\(\therefore 1+\cos{A}=2\cos^2{\frac{A}{2}}\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}}\)
আবার,
\(1-\cos{2A}=2\sin^2{A} ........(5)\)
\((5)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(1-\cos{\left(2\times\frac{A}{2}\right)}=2\sin^2{\frac{A}{2}}\)
\(\therefore 1-\cos{A}=2\sin^2{\frac{A}{2}}\)
\(1-\cos{A}=2\sin^2{\frac{A}{2}}\)
\(\cos{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\cos{A}\) in terms of \(\tan{\frac{A}{2}}\)
\(\cos{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)
\(\frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)
প্রমাণঃ
আমরা জানি,
\(\cos{2A}=\frac{1-\tan^2{A}}{1+\tan^2{A}} .......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\therefore \cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
আবার,
\(1-\cos{A}=2\sin^2{\frac{A}{2}} ........(2)\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}} ........(3)\)
\((2)\) কে \((3)\) দ্বারা ভাগ করে,
\(\frac{1-\cos{A}}{1+\cos{A}}=\frac{2\sin^2{\frac{A}{2}}}{2\cos^2{\frac{A}{2}}} \)
\(\Rightarrow \frac{1-\cos{A}}{1+\cos{A}}=\frac{\sin^2{\frac{A}{2}}}{\cos^2{\frac{A}{2}}} \)
\(\therefore \frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)➜ \(\because \frac{\sin{P}}{\cos{P}}=\tan{P}\)
\(\frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)
আমরা জানি,
\(\cos{2A}=\frac{1-\tan^2{A}}{1+\tan^2{A}} .......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cos{\left(2\times\frac{A}{2}\right)}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\therefore \cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
\(\cos{A}=\frac{1-\tan^2{\frac{A}{2}}}{1+\tan^2{\frac{A}{2}}}\)
আবার,
\(1-\cos{A}=2\sin^2{\frac{A}{2}} ........(2)\)
\(1+\cos{A}=2\cos^2{\frac{A}{2}} ........(3)\)
\((2)\) কে \((3)\) দ্বারা ভাগ করে,
\(\frac{1-\cos{A}}{1+\cos{A}}=\frac{2\sin^2{\frac{A}{2}}}{2\cos^2{\frac{A}{2}}} \)
\(\Rightarrow \frac{1-\cos{A}}{1+\cos{A}}=\frac{\sin^2{\frac{A}{2}}}{\cos^2{\frac{A}{2}}} \)
\(\therefore \frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)➜ \(\because \frac{\sin{P}}{\cos{P}}=\tan{P}\)
\(\frac{1-\cos{A}}{1+\cos{A}}=\tan^2{\frac{A}{2}}\)
\(\tan{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\tan{A}\) in terms of \(\tan{\frac{A}{2}}\)
\(\tan{A}\) কে \(\tan{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
প্রমাণঃ
আমরা জানি,
\(\tan{2A}=\frac{2\tan{A}}{1-\tan^2{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\tan{\left(2\times\frac{A}{2}\right)}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
\(\therefore \tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
\(\tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
আমরা জানি,
\(\tan{2A}=\frac{2\tan{A}}{1-\tan^2{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\tan{\left(2\times\frac{A}{2}\right)}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
\(\therefore \tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
\(\tan{A}=\frac{2\tan{\frac{A}{2}}}{1-\tan^2{\frac{A}{2}}}\)
\(\cot{A}\) কে \(\cot{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
Expressing \(\cot{A}\) in terms of \(\cot{\frac{A}{2}}\)
\(\cot{A}\) কে \(\cot{\frac{A}{2}}\) এর মাধ্যমে প্রকাশ
\(\cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
প্রমাণঃ
আমরা জানি,
\(\cot{2A}=\frac{\cot^2{A}-1}{2\cot{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cot{\left(2\times\frac{A}{2}\right)}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
\(\therefore \cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
\(\cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
আমরা জানি,
\(\cot{2A}=\frac{\cot^2{A}-1}{2\cot{A}} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cot{\left(2\times\frac{A}{2}\right)}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
\(\therefore \cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
\(\cot{A}=\frac{\cot^2{\frac{A}{2}}-1}{2\cot{\frac{A}{2}}}\)
\(\sin{A}\) কে \(\sin{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
Expressing \(\sin{A}\) in terms of \(\sin{\frac{A}{3}}\)
\(\sin{A}\) কে \(\sin{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
\(\sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
প্রমাণঃ
আমরা জানি,
\(\sin{3A}=3\sin{A}-4\sin^3{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\sin{\left(3\times\frac{A}{3}\right)}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
\(\therefore \sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
\(\sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
আমরা জানি,
\(\sin{3A}=3\sin{A}-4\sin^3{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\sin{\left(3\times\frac{A}{3}\right)}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
\(\therefore \sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
\(\sin{A}=3\sin{\frac{A}{3}}-4\sin^3{\frac{A}{3}}\)
\(\cos{A}\) কে \(\cos{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
Expressing \(\cos{A}\) in terms of \(\cos{\frac{A}{3}}\)
\(\cos{A}\) কে \(\cos{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
\(\cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
প্রমাণঃ
আমরা জানি,
\(\cos{3A}=4\cos^3{A}-3\cos{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\cos{\left(3\times\frac{A}{3}\right)}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
\(\therefore \cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
\(\cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
আমরা জানি,
\(\cos{3A}=4\cos^3{A}-3\cos{A} ........(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\cos{\left(3\times\frac{A}{3}\right)}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
\(\therefore \cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
\(\cos{A}=4\cos^3{\frac{A}{3}}-3\cos{\frac{A}{3}}\)
\(\tan{A}\) কে \(\tan{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
Expressing \(\tan{A}\) in terms of \(\tan{\frac{A}{3}}\)
\(\tan{A}\) কে \(\tan{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
\(\tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
প্রমাণঃ
আমরা জানি,
\(\tan{3A}=\frac{3\tan{A}-\tan^3{A}}{1-3\tan^2{A}} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\tan{\left(3\times\frac{A}{3}\right)}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
\(\therefore \tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
\(\tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
আমরা জানি,
\(\tan{3A}=\frac{3\tan{A}-\tan^3{A}}{1-3\tan^2{A}} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\tan{\left(3\times\frac{A}{3}\right)}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
\(\therefore \tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
\(\tan{A}=\frac{3\tan{\frac{A}{3}}-\tan^3{\frac{A}{3}}}{1-3\tan^2{\frac{A}{3}}}\)
\(\cot{A}\) কে \(\cot{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
Expressing \(\cot{A}\) in terms of \(\cot{\frac{A}{3}}\)
\(\cot{A}\) কে \(\cot{\frac{A}{3}}\) এর মাধ্যমে প্রকাশ
\(\cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{\frac{A}{3}}}{3\cot^2{\frac{A}{3}}-1}\)
প্রমাণঃ
আমরা জানি,
\(\cot{3A}=\frac{\cot^3{A}-3\cot{A}}{3\cot^2{A}-1} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\cot{\left(3\times\frac{A}{3}\right)}=\frac{\cot^3{\frac{A}{3}}-3\cot{A}}{3\cot^2{\frac{A}{3}}-1}\)
\(\therefore \cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{A}}{3\cot^2{\frac{A}{3}}-1}\)
\(\cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{\frac{A}{3}}}{3\cot^2{\frac{A}{3}}-1}\)
আমরা জানি,
\(\cot{3A}=\frac{\cot^3{A}-3\cot{A}}{3\cot^2{A}-1} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{3}\) বসিয়ে,
\(\cot{\left(3\times\frac{A}{3}\right)}=\frac{\cot^3{\frac{A}{3}}-3\cot{A}}{3\cot^2{\frac{A}{3}}-1}\)
\(\therefore \cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{A}}{3\cot^2{\frac{A}{3}}-1}\)
\(\cot{A}=\frac{\cot^3{\frac{A}{3}}-3\cot{\frac{A}{3}}}{3\cot^2{\frac{A}{3}}-1}\)
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}\) কে \(\cot{A}\) এর মাধ্যমে প্রকাশ
Expressing \(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}\) in terms of \(\cot{A}\)
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
প্রমাণঃ
আমরা জানি,
\(\cot{A}-\tan{A}=2\cot{2A} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{\left(2\times\frac{A}{2}\right)}\)
\(\therefore \cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
আমরা জানি,
\(\cot{A}-\tan{A}=2\cot{2A} ......(1)\)
\((1)\) নং সমীকরণে,
\(A\) এর স্থানে \(\frac{A}{2}\) বসিয়ে,
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{\left(2\times\frac{A}{2}\right)}\)
\(\therefore \cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
\(\cot{\frac{A}{2}}-\tan{\frac{A}{2}}=2\cot{A}\)
\(15^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(15^{o}\)
\(15^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\tan{15^{o}}=2-\sqrt{3}\)
\(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\tan{15^{o}}=2-\sqrt{3}\)
\(cosec \ {15^{o}}=\sqrt{6}+\sqrt{2}\)
\(\sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
\(\cot{15^{o}}=2+\sqrt{3}\)
\(\sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
\(\cot{15^{o}}=2+\sqrt{3}\)
প্রমাণঃ
আমরা জানি,
\(\sin{15^{o}}=\sin{(45^{o}-30^{o})}\)
\(\Rightarrow \sin{15^{o}}=\sin{45^{o}}\cos{30^{o}}-\cos{45^{o}}\sin{30^{o}}\) ➜ \(\because \sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\Rightarrow \sin{15^{o}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\times\frac{1}{2}\) ➜ \(\because \sin{45^{o}}=\cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
এবং \(\sin{30^{o}}=\frac{1}{2}\)
\(\Rightarrow \sin{15^{o}}=\frac{\sqrt{3}}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}\)
\(\therefore \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
আবার,
\(\cos{15^{o}}=\sqrt{1-\sin^2{15^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(15^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left(\frac{\sqrt{3}-1}{2\sqrt{2}}\right)^2}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\sqrt{1-\frac{(\sqrt{3}-1)^2}{(2\sqrt{2})^2}}\)
\(=\sqrt{1-\frac{3+1-2\sqrt{3}}{8}}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\sqrt{1-\frac{4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{8-4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{3+1+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{(\sqrt{3}+1)^2}{8}}\) ➜ \(\because a^2+b^2+2ab=(a+b)^2\)
\(=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\therefore \cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
আবার,
\(\tan{15^{o}}=\frac{\sin{15^{o}}}{\cos{15^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{\sqrt{3}-1}{2\sqrt{2}}}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
এবং \(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\) ➜ লব ও হরকে \(2\sqrt{2}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \tan{15^{o}}=2-\sqrt{3}\)
\(\tan{15^{o}}=\tan{(45^{o}-30^{o})}\)
\(=\frac{\tan{45^{o}}-\tan{30^{o}}}{1+\tan{45^{o}}\tan{30^{o}}}\) ➜ \(\because \tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
\(=\frac{1-\frac{1}{\sqrt{3}}}{1+1\times\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{45^{o}}=1\)
এবং \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\) ➜ লব ও হরকে \(\sqrt{3}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \tan{15^{o}}=2-\sqrt{3}\)
\(\tan{15^{o}}=2-\sqrt{3}\)
আবার,
\(cosec \ {15^{o}}=\frac{1}{\sin{15^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}-1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{2}\)
\(=\sqrt{2}(\sqrt{3}+1)\)
\(=\sqrt{6}+\sqrt{2}\)
\(\therefore cosec \ {15^{o}}=\sqrt{6}+\sqrt{2}\)
\(cosec \ {15^{o}}=\sqrt{6}+\sqrt{2}\)
আবার,
\(\sec{15^{o}}=\frac{1}{\cos{15^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}+1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{2}\)
\(=\sqrt{2}(\sqrt{3}-1)\)
\(=\sqrt{6}-\sqrt{2}\)
\(\therefore \sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
\(\sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
আমরা জানি,
\(\cot{15^{o}}=\cot{(45^{o}-30^{o})}\)
\(=\frac{\cot{45^{o}}\cot{30^{o}}+1}{\cot{30^{o}}-\cot{45^{o}}}\) ➜ \(\because \cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
\(=\frac{1\times\sqrt{3}+1}{\sqrt{3}-1}\) ➜ \(\because \cot{45^{o}}=1\)
এবং \(\cot{30^{o}}=\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \cot{15^{o}}=2+\sqrt{3}\)
\(\cot{15^{o}}=2+\sqrt{3}\)
আমরা জানি,
\(\sin{15^{o}}=\sin{(45^{o}-30^{o})}\)
\(\Rightarrow \sin{15^{o}}=\sin{45^{o}}\cos{30^{o}}-\cos{45^{o}}\sin{30^{o}}\) ➜ \(\because \sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\Rightarrow \sin{15^{o}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\times\frac{1}{2}\) ➜ \(\because \sin{45^{o}}=\cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
এবং \(\sin{30^{o}}=\frac{1}{2}\)
\(\Rightarrow \sin{15^{o}}=\frac{\sqrt{3}}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}\)
\(\therefore \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
আবার,
\(\cos{15^{o}}=\sqrt{1-\sin^2{15^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(15^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left(\frac{\sqrt{3}-1}{2\sqrt{2}}\right)^2}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\sqrt{1-\frac{(\sqrt{3}-1)^2}{(2\sqrt{2})^2}}\)
\(=\sqrt{1-\frac{3+1-2\sqrt{3}}{8}}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\sqrt{1-\frac{4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{8-4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{3+1+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{(\sqrt{3}+1)^2}{8}}\) ➜ \(\because a^2+b^2+2ab=(a+b)^2\)
\(=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\therefore \cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
আবার,
\(\tan{15^{o}}=\frac{\sin{15^{o}}}{\cos{15^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{\sqrt{3}-1}{2\sqrt{2}}}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
এবং \(\cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\) ➜ লব ও হরকে \(2\sqrt{2}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \tan{15^{o}}=2-\sqrt{3}\)
বিকল্প পদ্ধতিঃ
আমরা জানি, \(\tan{15^{o}}=\tan{(45^{o}-30^{o})}\)
\(=\frac{\tan{45^{o}}-\tan{30^{o}}}{1+\tan{45^{o}}\tan{30^{o}}}\) ➜ \(\because \tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
\(=\frac{1-\frac{1}{\sqrt{3}}}{1+1\times\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{45^{o}}=1\)
এবং \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\) ➜ লব ও হরকে \(\sqrt{3}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \tan{15^{o}}=2-\sqrt{3}\)
\(\tan{15^{o}}=2-\sqrt{3}\)
আবার,
\(cosec \ {15^{o}}=\frac{1}{\sin{15^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \sin{15^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}-1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{2}\)
\(=\sqrt{2}(\sqrt{3}+1)\)
\(=\sqrt{6}+\sqrt{2}\)
\(\therefore cosec \ {15^{o}}=\sqrt{6}+\sqrt{2}\)
\(cosec \ {15^{o}}=\sqrt{6}+\sqrt{2}\)
আবার,
\(\sec{15^{o}}=\frac{1}{\cos{15^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \cos{15^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}+1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{2}\)
\(=\sqrt{2}(\sqrt{3}-1)\)
\(=\sqrt{6}-\sqrt{2}\)
\(\therefore \sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
\(\sec{15^{o}}=\sqrt{6}-\sqrt{2}\)
আমরা জানি,
\(\cot{15^{o}}=\cot{(45^{o}-30^{o})}\)
\(=\frac{\cot{45^{o}}\cot{30^{o}}+1}{\cot{30^{o}}-\cot{45^{o}}}\) ➜ \(\because \cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
\(=\frac{1\times\sqrt{3}+1}{\sqrt{3}-1}\) ➜ \(\because \cot{45^{o}}=1\)
এবং \(\cot{30^{o}}=\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \cot{15^{o}}=2+\sqrt{3}\)
\(\cot{15^{o}}=2+\sqrt{3}\)
\(18^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(18^{o}\)
\(18^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(cosec \ {18^{o}}=\sqrt{5}+1\)
\(\sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
প্রমাণঃ
ধরি,
\(\theta=18^{o}\)
\(\Rightarrow 5\theta=5\times18^{o}\)
\(\Rightarrow 5\theta=90^{o}\)
\(\Rightarrow 2\theta+3\theta=90^{o}\)
\(\Rightarrow 2\theta=90^{o}-3\theta\)
\(\Rightarrow \sin{2\theta}=\sin{(90^{o}-3\theta)}\)
\(\Rightarrow \sin{2\theta}=\sin{(90^{o}\times1-3\theta)}\)
\(\Rightarrow \sin{2\theta}=\cos{3\theta}\) ➜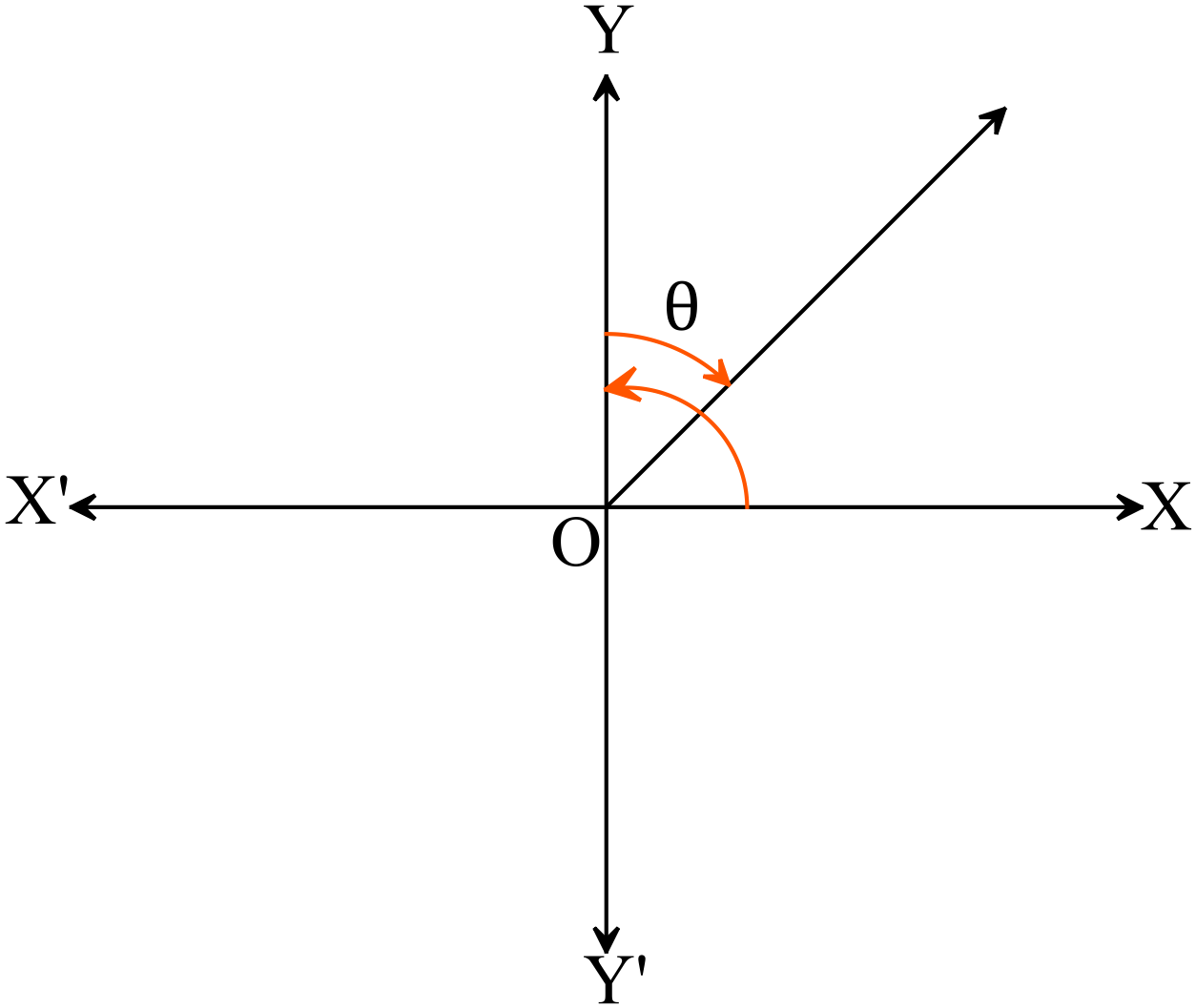
\(\because\) কোণ উৎপন্নকারী রেখাটি প্রথম চতুর্ভাগে অবস্থিত
সুতরাং সাইন অনুপাত ধনাত্মক।
আবার, \(90^{o}\) এর সহগুণক \(1\) একটি বিজোড় সংখ্যা,
সুতরাং সাইন অনুপাতের পরিবর্তন হয়ে কোসাইন হয়েছে।
\(\Rightarrow 2\sin{\theta}\cos{\theta}=4\cos^3{\theta}-3\cos{\theta}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(\cos{3A}=4\cos^3{A}-3\cos{A}\)
\(\Rightarrow 2\sin{\theta}\cos{\theta}=\cos{\theta}(4\cos^2{\theta}-3)\)
\(\Rightarrow 2\sin{\theta}=4\cos^2{\theta}-3\)
\(\Rightarrow 2\sin{\theta}=4(1-\sin^2{\theta})-3\) ➜ \(\because \cos^2{A}=1-\sin^2{A}\)
\(\Rightarrow 2\sin{\theta}=4-4\sin^2{\theta}-3\)
\(\Rightarrow 2\sin{\theta}=1-4\sin^2{\theta}\)
\(\Rightarrow 4\sin^2{\theta}+2\sin{\theta}-1=0\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{2^2-4\times4\times(-1)}}}{2\times4}\) ➜ \(\because ax^2+bx+c=0\)
\(\Rightarrow x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{4+16}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{20}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{4\times5}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{2\sqrt{5}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{2(-1\pm{\sqrt{5}})}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-1\pm{\sqrt{5}}}{4}\)
\(\Rightarrow \sin{18^{o}}=\frac{-1+\sqrt{5}}{4}\) ➜ \(\because 18^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
তাই \(\sin{18^{o}}\) এর মান ধনাত্মক হবে।
\(\therefore \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
আবার,
\(\cos{18^{o}}=\sqrt{1-\sin^2{18^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(18^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}(\sqrt{5}-1)\right\}^2}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\sqrt{1-\frac{1}{16}(\sqrt{5}-1)^2}\)
\(=\sqrt{\frac{1}{16}\{16-(\sqrt{5}-1)^2\}}\)
\(=\frac{1}{4}\sqrt{16-(5+1-2\sqrt{5})}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{4}\sqrt{16-(6-2\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{16-6+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\therefore \cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
আবার,
\(\tan{18^{o}}=\frac{\sin{18^{o}}}{\cos{18^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}(\sqrt{5}-1)}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
এবং \(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{\sqrt{5}-1}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{(\sqrt{5}-1)\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{5}-1)\sqrt{2\sqrt{5}(\sqrt{5}-1)}}{\sqrt{100-20}}\) ➜ \(\because \sqrt{10-2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}-1)}\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}-1)^2}}{\sqrt{80}}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1-2\sqrt{5})}}{4\sqrt{5}}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \(\sqrt{80}=4\sqrt{5}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-1)(3-\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}-3-5+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}-8)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-2)}}{2\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(\sqrt{5}-2)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{(5-2\sqrt{5})}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{25-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\therefore \tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
আবার,
\(cosec \ {18^{o}}=\frac{1}{\sin{18^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{4}{\sqrt{5}-1}\)
\(=\frac{4(\sqrt{5}+1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}+1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}+1)}{4}\)
\(=\sqrt{5}+1\)
\(\therefore cosec \ {18^{o}}=\sqrt{5}+1\)
\(cosec \ {18^{o}}=\sqrt{5}+1\)
আবার,
\(\sec{18^{o}}=\frac{1}{\cos{18^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{4\sqrt{5}}\)➜ \(\because \sqrt{80}=4\sqrt{5}\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\therefore \sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
আবার,
\(\cot{18^{o}}=\frac{1}{\tan{18^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\frac{1}{5}\sqrt{25-10\sqrt{5}}}\) ➜ \(\because \tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(=\frac{5}{\sqrt{25-10\sqrt{5}}}\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{25+10\sqrt{5}}\times\sqrt{25-10\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{25+10\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{625-500}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{125}}\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{5\sqrt{5}}\)➜ \(\because \sqrt{125}=5\sqrt{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\sqrt{5+2\sqrt{5}}\)
\(\therefore \cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
ধরি,
\(\theta=18^{o}\)
\(\Rightarrow 5\theta=5\times18^{o}\)
\(\Rightarrow 5\theta=90^{o}\)
\(\Rightarrow 2\theta+3\theta=90^{o}\)
\(\Rightarrow 2\theta=90^{o}-3\theta\)
\(\Rightarrow \sin{2\theta}=\sin{(90^{o}-3\theta)}\)
\(\Rightarrow \sin{2\theta}=\sin{(90^{o}\times1-3\theta)}\)
\(\Rightarrow \sin{2\theta}=\cos{3\theta}\) ➜
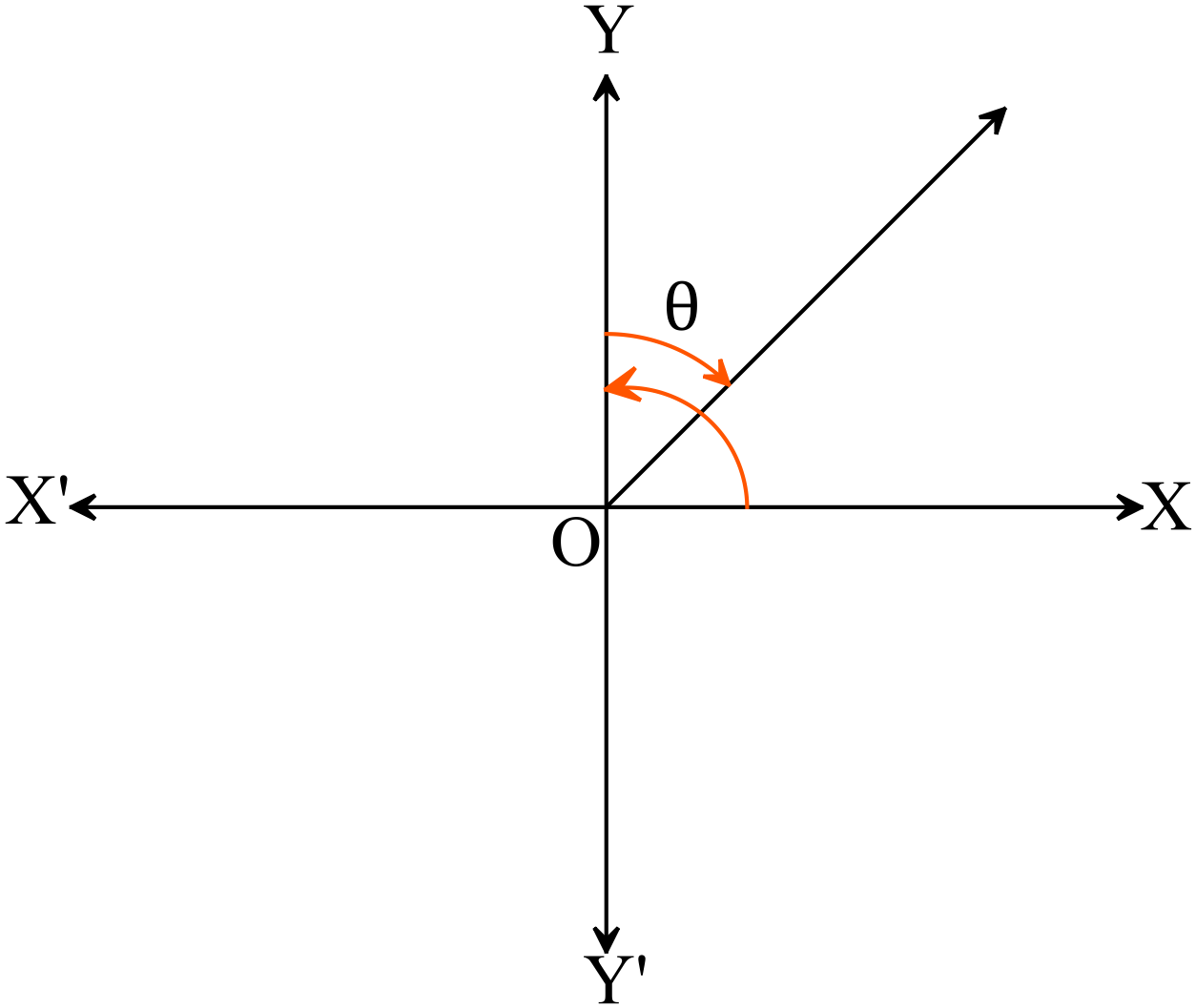
\(\because\) কোণ উৎপন্নকারী রেখাটি প্রথম চতুর্ভাগে অবস্থিত
সুতরাং সাইন অনুপাত ধনাত্মক।
আবার, \(90^{o}\) এর সহগুণক \(1\) একটি বিজোড় সংখ্যা,
সুতরাং সাইন অনুপাতের পরিবর্তন হয়ে কোসাইন হয়েছে।
\(\Rightarrow 2\sin{\theta}\cos{\theta}=4\cos^3{\theta}-3\cos{\theta}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(\cos{3A}=4\cos^3{A}-3\cos{A}\)
\(\Rightarrow 2\sin{\theta}\cos{\theta}=\cos{\theta}(4\cos^2{\theta}-3)\)
\(\Rightarrow 2\sin{\theta}=4\cos^2{\theta}-3\)
\(\Rightarrow 2\sin{\theta}=4(1-\sin^2{\theta})-3\) ➜ \(\because \cos^2{A}=1-\sin^2{A}\)
\(\Rightarrow 2\sin{\theta}=4-4\sin^2{\theta}-3\)
\(\Rightarrow 2\sin{\theta}=1-4\sin^2{\theta}\)
\(\Rightarrow 4\sin^2{\theta}+2\sin{\theta}-1=0\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{2^2-4\times4\times(-1)}}}{2\times4}\) ➜ \(\because ax^2+bx+c=0\)
\(\Rightarrow x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{4+16}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{20}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{\sqrt{4\times5}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-2\pm{2\sqrt{5}}}{8}\)
\(\Rightarrow \sin{\theta}=\frac{2(-1\pm{\sqrt{5}})}{8}\)
\(\Rightarrow \sin{\theta}=\frac{-1\pm{\sqrt{5}}}{4}\)
\(\Rightarrow \sin{18^{o}}=\frac{-1+\sqrt{5}}{4}\) ➜ \(\because 18^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
তাই \(\sin{18^{o}}\) এর মান ধনাত্মক হবে।
\(\therefore \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
আবার,
\(\cos{18^{o}}=\sqrt{1-\sin^2{18^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(18^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}(\sqrt{5}-1)\right\}^2}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\sqrt{1-\frac{1}{16}(\sqrt{5}-1)^2}\)
\(=\sqrt{\frac{1}{16}\{16-(\sqrt{5}-1)^2\}}\)
\(=\frac{1}{4}\sqrt{16-(5+1-2\sqrt{5})}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{4}\sqrt{16-(6-2\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{16-6+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\therefore \cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
আবার,
\(\tan{18^{o}}=\frac{\sin{18^{o}}}{\cos{18^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}(\sqrt{5}-1)}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
এবং \(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{\sqrt{5}-1}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{(\sqrt{5}-1)\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{5}-1)\sqrt{2\sqrt{5}(\sqrt{5}-1)}}{\sqrt{100-20}}\) ➜ \(\because \sqrt{10-2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}-1)}\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}-1)^2}}{\sqrt{80}}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1-2\sqrt{5})}}{4\sqrt{5}}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \(\sqrt{80}=4\sqrt{5}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-1)(3-\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}-3-5+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}-8)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-2)}}{2\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(\sqrt{5}-2)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{(5-2\sqrt{5})}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{25-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\therefore \tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
আবার,
\(cosec \ {18^{o}}=\frac{1}{\sin{18^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{4}{\sqrt{5}-1}\)
\(=\frac{4(\sqrt{5}+1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}+1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}+1)}{4}\)
\(=\sqrt{5}+1\)
\(\therefore cosec \ {18^{o}}=\sqrt{5}+1\)
\(cosec \ {18^{o}}=\sqrt{5}+1\)
আবার,
\(\sec{18^{o}}=\frac{1}{\cos{18^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{4\sqrt{5}}\)➜ \(\because \sqrt{80}=4\sqrt{5}\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\therefore \sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\sec{18^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
আবার,
\(\cot{18^{o}}=\frac{1}{\tan{18^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\frac{1}{5}\sqrt{25-10\sqrt{5}}}\) ➜ \(\because \tan{18^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(=\frac{5}{\sqrt{25-10\sqrt{5}}}\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{25+10\sqrt{5}}\times\sqrt{25-10\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{25+10\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{625-500}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{\sqrt{125}}\)
\(=\frac{5\sqrt{25+10\sqrt{5}}}{5\sqrt{5}}\)➜ \(\because \sqrt{125}=5\sqrt{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\sqrt{5+2\sqrt{5}}\)
\(\therefore \cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\cot{18^{o}}=\sqrt{5+2\sqrt{5}}\)
\(36^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(36^{o}\)
\(36^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(cosec \ {36^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\sec{36^{o}}=\sqrt{5}-1\)
\(\cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\sec{36^{o}}=\sqrt{5}-1\)
\(\cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
প্রমাণঃ
লেখা যায়,
\(\sin{36^{o}}=\sin{(2\times18^{o})}\)
\(=2\sin{18^{o}}\cos{18^{o}}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(=2\times\frac{1}{4}(\sqrt{5}-1)\times\frac{1}{4}\sqrt{10+2\sqrt{5}}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{1}{8}(\sqrt{5}-1)\sqrt{10+2\sqrt{5}}\)
\(=\frac{1}{8}(\sqrt{5}-1)\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}-1)^2}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1-2\sqrt{5})}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(6-2\sqrt{5})}\)
\(=\frac{1}{8}\sqrt{4\sqrt{5}(\sqrt{5}+1)(3-\sqrt{5})}\)
\(=\frac{2}{8}\sqrt{\sqrt{5}(3\sqrt{5}+3-5-\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{\sqrt{5}(2\sqrt{5}-2)}\)
\(=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\therefore \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
আবার,
\(\cos{36^{o}}=\sqrt{1-\sin^2{36^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(36^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}\sqrt{10-2\sqrt{5}}\right\}^2}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\sqrt{1-\frac{1}{16}(10-2\sqrt{5})}\)
\(=\sqrt{\frac{1}{16}\{16-(10-2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-10+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{6+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{5+1+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{(\sqrt{5}+1)^2}\) ➜ \(\because a^2+b^2+2ab=(a+b)^2\)
\(=\frac{1}{4}(\sqrt{5}+1)\)
\(\therefore \cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
আবার,
\(\tan{36^{o}}=\frac{\sin{36^{o}}}{\cos{36^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}\sqrt{10-2\sqrt{5}}}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
এবং \(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}+1}\)
\(=\frac{(\sqrt{5}-1)\sqrt{10-2\sqrt{5}}}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}-1)^2}}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10-2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}-1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1-2\sqrt{5})}}{4}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(6-2\sqrt{5})}}{4}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-1)(3-\sqrt{5})}}{4}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}-3-5+\sqrt{5})}}{4}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}-8)}}{2}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-2)}}{2}\)
\(=\frac{2\sqrt{5-2\sqrt{5}}}{2}\)
\(=\sqrt{5-2\sqrt{5}}\)
\(\therefore \tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
আবার,
\(cosec \ {36^{o}}=\frac{1}{\sin{36^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\therefore cosec \ {36^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(cosec \ {36^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
আবার,
\(\sec{36^{o}}=\frac{1}{\cos{36^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{4}{\sqrt{5}+1}\)
\(=\frac{4(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}-1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}-1)}{4}\)
\(=\sqrt{5}-1\)
\(\therefore \sec{36^{o}}=\sqrt{5}-1\)
\(\sec{36^{o}}=\sqrt{5}-1\)
আবার,
\(\cot{36^{o}}=\frac{1}{\tan{36^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\sqrt{5-2\sqrt{5}}}\) ➜ \(\because \tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5+2\sqrt{5}}\times\sqrt{5-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{5+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{25-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\therefore \cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
লেখা যায়,
\(\sin{36^{o}}=\sin{(2\times18^{o})}\)
\(=2\sin{18^{o}}\cos{18^{o}}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(=2\times\frac{1}{4}(\sqrt{5}-1)\times\frac{1}{4}\sqrt{10+2\sqrt{5}}\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\cos{18^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{1}{8}(\sqrt{5}-1)\sqrt{10+2\sqrt{5}}\)
\(=\frac{1}{8}(\sqrt{5}-1)\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}-1)^2}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1-2\sqrt{5})}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}+1)(6-2\sqrt{5})}\)
\(=\frac{1}{8}\sqrt{4\sqrt{5}(\sqrt{5}+1)(3-\sqrt{5})}\)
\(=\frac{2}{8}\sqrt{\sqrt{5}(3\sqrt{5}+3-5-\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{\sqrt{5}(2\sqrt{5}-2)}\)
\(=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\therefore \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
আবার,
\(\cos{36^{o}}=\sqrt{1-\sin^2{36^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(36^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}\sqrt{10-2\sqrt{5}}\right\}^2}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\sqrt{1-\frac{1}{16}(10-2\sqrt{5})}\)
\(=\sqrt{\frac{1}{16}\{16-(10-2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-10+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{6+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{5+1+2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{(\sqrt{5}+1)^2}\) ➜ \(\because a^2+b^2+2ab=(a+b)^2\)
\(=\frac{1}{4}(\sqrt{5}+1)\)
\(\therefore \cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
আবার,
\(\tan{36^{o}}=\frac{\sin{36^{o}}}{\cos{36^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}\sqrt{10-2\sqrt{5}}}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
এবং \(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}+1}\)
\(=\frac{(\sqrt{5}-1)\sqrt{10-2\sqrt{5}}}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}-1)^2}}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10-2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}-1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1-2\sqrt{5})}}{4}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}-1)(6-2\sqrt{5})}}{4}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-1)(3-\sqrt{5})}}{4}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}-3-5+\sqrt{5})}}{4}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}-8)}}{2}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}-2)}}{2}\)
\(=\frac{2\sqrt{5-2\sqrt{5}}}{2}\)
\(=\sqrt{5-2\sqrt{5}}\)
\(\therefore \tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
আবার,
\(cosec \ {36^{o}}=\frac{1}{\sin{36^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\therefore cosec \ {36^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(cosec \ {36^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
আবার,
\(\sec{36^{o}}=\frac{1}{\cos{36^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{4}{\sqrt{5}+1}\)
\(=\frac{4(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}-1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}-1)}{4}\)
\(=\sqrt{5}-1\)
\(\therefore \sec{36^{o}}=\sqrt{5}-1\)
\(\sec{36^{o}}=\sqrt{5}-1\)
আবার,
\(\cot{36^{o}}=\frac{1}{\tan{36^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\sqrt{5-2\sqrt{5}}}\) ➜ \(\because \tan{36^{o}}=\sqrt{5-2\sqrt{5}}\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5+2\sqrt{5}}\times\sqrt{5-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{5+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{25-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\therefore \cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\cot{36^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(54^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(54^{o}\)
\(54^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(cosec \ {54^{o}}=\sqrt{5}-1\)
\(\sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
প্রমাণঃ
লেখা যায়,
\(\sin{54^{o}}=\sin{(3\times18^{o})}\)
\(=3\sin{18^{o}}-4\sin^3{18^{o}}\) ➜ \(\because \sin{3A}=3\sin{A}-4\sin^3{A}\)
\(=3\times\frac{1}{4}(\sqrt{5}-1)-4\times\left\{\frac{1}{4}(\sqrt{5}-1)\right\}^3\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{3}{4}(\sqrt{5}-1)-4\times\frac{1}{64}(\sqrt{5}-1)^3\)
\(=\frac{3}{4}(\sqrt{5}-1)-\frac{1}{16}(\sqrt{5}-1)^3\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(\sqrt{5}-1)^2\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(5+1-2\sqrt{5})\right\}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(6-2\sqrt{5})\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-6+2\sqrt{5}\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{6+2\sqrt{5}\right\}\)
\(=\frac{2}{16}(\sqrt{5}-1)(3+\sqrt{5})\)
\(=\frac{1}{8}(3\sqrt{5}-3+5-\sqrt{5})\)
\(=\frac{1}{8}(2\sqrt{5}+2)\)
\(=\frac{2}{8}(\sqrt{5}+1)\)
\(=\frac{1}{4}(\sqrt{5}+1)\)
\(\therefore \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
আবার,
\(\cos{54^{o}}=\sqrt{1-\sin^2{54^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(54^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}(\sqrt{5}+1)\right\}^2}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\sqrt{1-\frac{1}{16}(\sqrt{5}+1)^2}\)
\(=\sqrt{\frac{1}{16}\{16-(\sqrt{5}+1)^2\}}\)
\(=\frac{1}{4}\sqrt{\{16-(5+1+2\sqrt{5})\}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{1}{4}\sqrt{\{16-(6+2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-6-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\therefore \cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
আবার,
\(\tan{54^{o}}=\frac{\sin{54^{o}}}{\cos{54^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}(\sqrt{5}+1)}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
এবং \(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{\sqrt{5}+1}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{(\sqrt{5}+1)\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{5}+1)\sqrt{2\sqrt{5}(\sqrt{5}+1)}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10+2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}+1)^2}}{\sqrt{80}}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1+2\sqrt{5})}}{4\sqrt{5}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(6+2\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+1)(3+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}+3+5+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}+8)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+2)}}{2\sqrt{5}}\)
\(=\frac{2\sqrt{5+2\sqrt{5}}}{2\sqrt{5}}\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\therefore \tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
আবার,
\(cosec \ {54^{o}}=\frac{1}{\sin{54^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{4}{\sqrt{5}+1}\)
\(=\frac{4(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}-1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}-1)}{4}\)
\(=\sqrt{5}-1\)
\(\therefore cosec \ {54^{o}}=\sqrt{5}-1\)
\(cosec \ {54^{o}}=\sqrt{5}-1\)
আবার,
\(\sec{54^{o}}=\frac{1}{\cos{54^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\therefore \sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
আবার,
\(\cot{54^{o}}=\frac{1}{\tan{54^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\frac{1}{5}\sqrt{25+10\sqrt{5}}}\) ➜ \(\because \tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(=\frac{5}{\sqrt{25+10\sqrt{5}}}\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{25+10\sqrt{5}}\times\sqrt{25-10\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{25-10\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{625-500}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{125}}\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{5\sqrt{5}}\)
\(=\frac{\sqrt{25-10\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5(5-2\sqrt{5})}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5-2\sqrt{5}}}{\sqrt{5}}\)
\(=\sqrt{5-2\sqrt{5}}\)
\(\therefore \cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
লেখা যায়,
\(\sin{54^{o}}=\sin{(3\times18^{o})}\)
\(=3\sin{18^{o}}-4\sin^3{18^{o}}\) ➜ \(\because \sin{3A}=3\sin{A}-4\sin^3{A}\)
\(=3\times\frac{1}{4}(\sqrt{5}-1)-4\times\left\{\frac{1}{4}(\sqrt{5}-1)\right\}^3\) ➜ \(\because \sin{18^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{3}{4}(\sqrt{5}-1)-4\times\frac{1}{64}(\sqrt{5}-1)^3\)
\(=\frac{3}{4}(\sqrt{5}-1)-\frac{1}{16}(\sqrt{5}-1)^3\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(\sqrt{5}-1)^2\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(5+1-2\sqrt{5})\right\}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-(6-2\sqrt{5})\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{12-6+2\sqrt{5}\right\}\)
\(=\frac{1}{16}(\sqrt{5}-1)\left\{6+2\sqrt{5}\right\}\)
\(=\frac{2}{16}(\sqrt{5}-1)(3+\sqrt{5})\)
\(=\frac{1}{8}(3\sqrt{5}-3+5-\sqrt{5})\)
\(=\frac{1}{8}(2\sqrt{5}+2)\)
\(=\frac{2}{8}(\sqrt{5}+1)\)
\(=\frac{1}{4}(\sqrt{5}+1)\)
\(\therefore \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(\sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
আবার,
\(\cos{54^{o}}=\sqrt{1-\sin^2{54^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(54^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}(\sqrt{5}+1)\right\}^2}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\sqrt{1-\frac{1}{16}(\sqrt{5}+1)^2}\)
\(=\sqrt{\frac{1}{16}\{16-(\sqrt{5}+1)^2\}}\)
\(=\frac{1}{4}\sqrt{\{16-(5+1+2\sqrt{5})\}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{1}{4}\sqrt{\{16-(6+2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-6-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\therefore \cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
আবার,
\(\tan{54^{o}}=\frac{\sin{54^{o}}}{\cos{54^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}(\sqrt{5}+1)}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
এবং \(\cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{\sqrt{5}+1}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{(\sqrt{5}+1)\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{5}+1)\sqrt{2\sqrt{5}(\sqrt{5}+1)}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10+2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}+1)^2}}{\sqrt{80}}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1+2\sqrt{5})}}{4\sqrt{5}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(6+2\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+1)(3+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}+3+5+\sqrt{5})}}{4\sqrt{5}}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}+8)}}{2\sqrt{5}}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+2)}}{2\sqrt{5}}\)
\(=\frac{2\sqrt{5+2\sqrt{5}}}{2\sqrt{5}}\)
\(=\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\therefore \tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(\tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
আবার,
\(cosec \ {54^{o}}=\frac{1}{\sin{54^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}+1)}\) ➜ \(\because \sin{54^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{4}{\sqrt{5}+1}\)
\(=\frac{4(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}-1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}-1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}-1)}{4}\)
\(=\sqrt{5}-1\)
\(\therefore cosec \ {54^{o}}=\sqrt{5}-1\)
\(cosec \ {54^{o}}=\sqrt{5}-1\)
আবার,
\(\sec{54^{o}}=\frac{1}{\cos{54^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10-2\sqrt{5}}}\) ➜ \(\because \cos{54^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10-2\sqrt{5}}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10+2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10+2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10+2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10+2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50+10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\therefore \sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
\(\sec{54^{o}}=\frac{1}{5}\sqrt{50+10\sqrt{5}}\)
আবার,
\(\cot{54^{o}}=\frac{1}{\tan{54^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\frac{1}{5}\sqrt{25+10\sqrt{5}}}\) ➜ \(\because \tan{54^{o}}=\frac{1}{5}\sqrt{25+10\sqrt{5}}\)
\(=\frac{5}{\sqrt{25+10\sqrt{5}}}\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{25+10\sqrt{5}}\times\sqrt{25-10\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{25-10\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{625-500}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{\sqrt{125}}\)
\(=\frac{5\sqrt{25-10\sqrt{5}}}{5\sqrt{5}}\)
\(=\frac{\sqrt{25-10\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5(5-2\sqrt{5})}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5-2\sqrt{5}}}{\sqrt{5}}\)
\(=\sqrt{5-2\sqrt{5}}\)
\(\therefore \cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
\(\cot{54^{o}}=\sqrt{5-2\sqrt{5}}\)
\(72^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(72^{o}\)
\(72^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(cosec \ {72^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\sec{72^{o}}=\sqrt{5}+1\)
\(\cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\sec{72^{o}}=\sqrt{5}+1\)
\(\cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
প্রমাণঃ
লেখা যায়,
\(\sin{72^{o}}=\sin{(2\times36^{o})}\)
\(=2\sin{36^{o}}\cos{36^{o}}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(=2\times\frac{1}{4}\sqrt{10-2\sqrt{5}}\times\frac{1}{4}(\sqrt{5}+1)\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{10-2\sqrt{5}}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}+1)^2}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1+2\sqrt{5})}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(6+2\sqrt{5})}\)
\(=\frac{1}{8}\sqrt{4\sqrt{5}(\sqrt{5}-1)(3+\sqrt{5})}\)
\(=\frac{2}{8}\sqrt{\sqrt{5}(3\sqrt{5}-3+5-\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{\sqrt{5}(2\sqrt{5}+2)}\)
\(=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\therefore \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
আবার,
\(\cos{72^{o}}=\sqrt{1-\sin^2{72^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(72^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}\sqrt{10+2\sqrt{5}}\right\}^2}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\sqrt{1-\frac{1}{16}(10+2\sqrt{5})}\)
\(=\sqrt{\frac{1}{16}\{16-(10+2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-10-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{6-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{5+1-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{(\sqrt{5}-1)^2}\) ➜ \(\because a^2+b^2-2ab=(a-b)^2\)
\(=\frac{1}{4}(\sqrt{5}-1)\)
\(\therefore \cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
আবার,
\(\tan{72^{o}}=\frac{\sin{72^{o}}}{\cos{72^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}\sqrt{10+2\sqrt{5}}}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
এবং \(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}-1}\)
\(=\frac{(\sqrt{5}+1)\sqrt{10+2\sqrt{5}}}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}+1)^2}}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10+2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1+2\sqrt{5})}}{4}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(6+2\sqrt{5})}}{4}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+1)(3+\sqrt{5})}}{4}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}+3+5+\sqrt{5})}}{4}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}+8)}}{2}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+2)}}{2}\)
\(=\frac{2\sqrt{5+2\sqrt{5}}}{2}\)
\(=\sqrt{5+2\sqrt{5}}\)
\(\therefore \tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
আবার,
\(cosec \ {72^{o}}=\frac{1}{\sin{72^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\therefore cosec \ {72^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(cosec \ {72^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
আবার,
\(\sec{72^{o}}=\frac{1}{\cos{72^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{4}{\sqrt{5}-1}\)
\(=\frac{4(\sqrt{5}+1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}+1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}+1)}{4}\)
\(=\sqrt{5}+1\)
\(\therefore \sec{72^{o}}=\sqrt{5}+1\)
\(\sec{72^{o}}=\sqrt{5}+1\)
আবার,
\(\cot{72^{o}}=\frac{1}{\tan{72^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\sqrt{5+2\sqrt{5}}}\) ➜ \(\because \tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{5+2\sqrt{5}}\times\sqrt{5-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{5-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{25-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\therefore \cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
লেখা যায়,
\(\sin{72^{o}}=\sin{(2\times36^{o})}\)
\(=2\sin{36^{o}}\cos{36^{o}}\) ➜ \(\because \sin{2A}=2\sin{A}\cos{A}\)
\(=2\times\frac{1}{4}\sqrt{10-2\sqrt{5}}\times\frac{1}{4}(\sqrt{5}+1)\) ➜ \(\because \sin{36^{o}}=\frac{1}{4}\sqrt{10-2\sqrt{5}}\)
\(\cos{36^{o}}=\frac{1}{4}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{10-2\sqrt{5}}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)}(\sqrt{5}+1)\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(\sqrt{5}+1)^2}\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(5+1+2\sqrt{5})}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{1}{8}\sqrt{2\sqrt{5}(\sqrt{5}-1)(6+2\sqrt{5})}\)
\(=\frac{1}{8}\sqrt{4\sqrt{5}(\sqrt{5}-1)(3+\sqrt{5})}\)
\(=\frac{2}{8}\sqrt{\sqrt{5}(3\sqrt{5}-3+5-\sqrt{5})}\)
\(=\frac{1}{4}\sqrt{\sqrt{5}(2\sqrt{5}+2)}\)
\(=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\therefore \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(\sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
আবার,
\(\cos{72^{o}}=\sqrt{1-\sin^2{72^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(72^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left\{\frac{1}{4}\sqrt{10+2\sqrt{5}}\right\}^2}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\sqrt{1-\frac{1}{16}(10+2\sqrt{5})}\)
\(=\sqrt{\frac{1}{16}\{16-(10+2\sqrt{5})\}}\)
\(=\frac{1}{4}\sqrt{16-10-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{6-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{5+1-2\sqrt{5}}\)
\(=\frac{1}{4}\sqrt{(\sqrt{5}-1)^2}\) ➜ \(\because a^2+b^2-2ab=(a-b)^2\)
\(=\frac{1}{4}(\sqrt{5}-1)\)
\(\therefore \cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
আবার,
\(\tan{72^{o}}=\frac{\sin{72^{o}}}{\cos{72^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{1}{4}\sqrt{10+2\sqrt{5}}}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
এবং \(\cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{\sqrt{10+2\sqrt{5}}}{\sqrt{5}-1}\)
\(=\frac{(\sqrt{5}+1)\sqrt{10+2\sqrt{5}}}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(\sqrt{5}+1)^2}}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
এবং \(\sqrt{10+2\sqrt{5}}=\sqrt{2\sqrt{5}(\sqrt{5}+1)}\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(5+1+2\sqrt{5})}}{4}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\frac{\sqrt{2\sqrt{5}(\sqrt{5}+1)(6+2\sqrt{5})}}{4}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+1)(3+\sqrt{5})}}{4}\)
\(=\frac{2\sqrt{\sqrt{5}(3\sqrt{5}+3+5+\sqrt{5})}}{4}\)
\(=\frac{\sqrt{\sqrt{5}(4\sqrt{5}+8)}}{2}\)
\(=\frac{\sqrt{4\sqrt{5}(\sqrt{5}+2)}}{2}\)
\(=\frac{2\sqrt{5+2\sqrt{5}}}{2}\)
\(=\sqrt{5+2\sqrt{5}}\)
\(\therefore \tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(\tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
আবার,
\(cosec \ {72^{o}}=\frac{1}{\sin{72^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{1}{4}\sqrt{10+2\sqrt{5}}}\) ➜ \(\because \sin{72^{o}}=\frac{1}{4}\sqrt{10+2\sqrt{5}}\)
\(=\frac{4}{\sqrt{10+2\sqrt{5}}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{10+2\sqrt{5}}\times\sqrt{10-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{10-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{100-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{\sqrt{80}}\)
\(=\frac{4\sqrt{10-2\sqrt{5}}}{4\sqrt{5}}\)
\(=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{10-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(10-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{50-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(\therefore cosec \ {72^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
\(cosec \ {72^{o}}=\frac{1}{5}\sqrt{50-10\sqrt{5}}\)
আবার,
\(\sec{72^{o}}=\frac{1}{\cos{72^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{1}{4}(\sqrt{5}-1)}\) ➜ \(\because \cos{72^{o}}=\frac{1}{4}(\sqrt{5}-1)\)
\(=\frac{4}{\sqrt{5}-1}\)
\(=\frac{4(\sqrt{5}+1)}{(\sqrt{5}+1)(\sqrt{5}-1)}\) ➜ লব ও হরকে \((\sqrt{5}+1)\) দ্বারা গুণ করে।
\(=\frac{4(\sqrt{5}+1)}{5-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{4(\sqrt{5}+1)}{4}\)
\(=\sqrt{5}+1\)
\(\therefore \sec{72^{o}}=\sqrt{5}+1\)
\(\sec{72^{o}}=\sqrt{5}+1\)
আবার,
\(\cot{72^{o}}=\frac{1}{\tan{72^{o}}}\) ➜ \(\because \cot{A}=\frac{1}{\tan{A}}\)
\(=\frac{1}{\sqrt{5+2\sqrt{5}}}\) ➜ \(\because \tan{72^{o}}=\sqrt{5+2\sqrt{5}}\)
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{5+2\sqrt{5}}\times\sqrt{5-2\sqrt{5}}}\) ➜ লব ও হরকে \(\sqrt{5-2\sqrt{5}}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{25-20}}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{\sqrt{5-2\sqrt{5}}}{\sqrt{5}}\)
\(=\frac{\sqrt{5}\sqrt{5-2\sqrt{5}}}{\sqrt{5}\times\sqrt{5}}\) ➜ লব ও হরকে \(\sqrt{5}\) দ্বারা গুণ করে।
\(=\frac{\sqrt{5(5-2\sqrt{5})}}{5}\)
\(=\frac{\sqrt{25-10\sqrt{5}}}{5}\)
\(=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\therefore \cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(\cot{72^{o}}=\frac{1}{5}\sqrt{25-10\sqrt{5}}\)
\(75^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of the angle \(75^{o}\)
\(75^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
\(\sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\tan{75^{o}}=2+\sqrt{3}\)
\(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\tan{75^{o}}=2+\sqrt{3}\)
\(cosec \ {75^{o}}=\sqrt{6}-\sqrt{2}\)
\(\sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
\(\cot{75^{o}}=2-\sqrt{3}\)
\(\sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
\(\cot{75^{o}}=2-\sqrt{3}\)
প্রমাণঃ
আমরা জানি,
\(\sin{75^{o}}=\sin{(45^{o}+30^{o})}\)
\(\Rightarrow \sin{75^{o}}=\sin{45^{o}}\cos{30^{o}}+\cos{45^{o}}\sin{30^{o}}\) ➜ \(\because \sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\Rightarrow \sin{75^{o}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}}\times\frac{1}{2}\) ➜ \(\because \sin{45^{o}}=\cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
এবং \(\sin{30^{o}}=\frac{1}{2}\)
\(\Rightarrow \sin{75^{o}}=\frac{\sqrt{3}}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}\)
\(\therefore \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
আবার,
\(\cos{75^{o}}=\sqrt{1-\sin^2{75^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(75^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left(\frac{\sqrt{3}+1}{2\sqrt{2}}\right)^2}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\sqrt{1-\frac{(\sqrt{3}+1)^2}{(2\sqrt{2})^2}}\)
\(=\sqrt{1-\frac{3+1+2\sqrt{3}}{8}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\sqrt{1-\frac{4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{8-4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{3+1-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{(\sqrt{3}-1)^2}{8}}\) ➜ \(\because a^2+b^2-2ab=(a-b)^2\)
\(=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\therefore \cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
আবার,
\(\tan{75^{o}}=\frac{\sin{75^{o}}}{\cos{75^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{\sqrt{3}+1}{2\sqrt{2}}}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
এবং \(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) ➜ লব ও হরকে \(2\sqrt{2}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \tan{75^{o}}=2+\sqrt{3}\)
\(\tan{75^{o}}=\tan{(45^{o}+30^{o})}\)
\(=\frac{\tan{45^{o}}+\tan{30^{o}}}{1-\tan{45^{o}}\tan{30^{o}}}\) ➜ \(\because \tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(=\frac{1+\frac{1}{\sqrt{3}}}{1-1\times\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{45^{o}}=1\)
এবং \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(=\frac{1+\frac{1}{\sqrt{3}}}{1-\frac{1}{\sqrt{3}}}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) ➜ লব ও হরকে \(\sqrt{3}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \tan{75^{o}}=2+\sqrt{3}\)
\(\tan{75^{o}}=2+\sqrt{3}\)
আবার,
\(cosec \ {75^{o}}=\frac{1}{\sin{75^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}+1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{2}\)
\(=\sqrt{2}(\sqrt{3}-1)\)
\(=\sqrt{6}-\sqrt{2}\)
\(\therefore cosec \ {75^{o}}=\sqrt{6}-\sqrt{2}\)
\(cosec \ {75^{o}}=\sqrt{6}-\sqrt{2}\)
আবার,
\(\sec{75^{o}}=\frac{1}{\cos{75^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}-1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{2}\)
\(=\sqrt{2}(\sqrt{3}+1)\)
\(=\sqrt{6}+\sqrt{2}\)
\(\therefore \sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
\(\sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
আমরা জানি,
\(\cot{75^{o}}=\cot{(45^{o}+30^{o})}\)
\(=\frac{\cot{45^{o}}\cot{30^{o}}-1}{\cot{30^{o}}+\cot{45^{o}}}\) ➜ \(\because \cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(=\frac{1\times\sqrt{3}-1}{\sqrt{3}+1}\) ➜ \(\because \cot{45^{o}}=1\)
এবং \(\cot{30^{o}}=\sqrt{3}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \cot{75^{o}}=2-\sqrt{3}\)
\(\cot{75^{o}}=2-\sqrt{3}\)
আমরা জানি,
\(\sin{75^{o}}=\sin{(45^{o}+30^{o})}\)
\(\Rightarrow \sin{75^{o}}=\sin{45^{o}}\cos{30^{o}}+\cos{45^{o}}\sin{30^{o}}\) ➜ \(\because \sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\Rightarrow \sin{75^{o}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}}\times\frac{1}{2}\) ➜ \(\because \sin{45^{o}}=\cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
এবং \(\sin{30^{o}}=\frac{1}{2}\)
\(\Rightarrow \sin{75^{o}}=\frac{\sqrt{3}}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}\)
\(\therefore \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(\sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
আবার,
\(\cos{75^{o}}=\sqrt{1-\sin^2{75^{o}}}\) ➜ \(\because \cos{A}=\sqrt{1-\sin^2{A}}\)
এবং \(75^{o}\) কোণ ধনাত্মক ও সূক্ষ্ণ।
\(=\sqrt{1-\left(\frac{\sqrt{3}+1}{2\sqrt{2}}\right)^2}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\sqrt{1-\frac{(\sqrt{3}+1)^2}{(2\sqrt{2})^2}}\)
\(=\sqrt{1-\frac{3+1+2\sqrt{3}}{8}}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
\(=\sqrt{1-\frac{4+2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{8-4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{4-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{3+1-2\sqrt{3}}{8}}\)
\(=\sqrt{\frac{(\sqrt{3}-1)^2}{8}}\) ➜ \(\because a^2+b^2-2ab=(a-b)^2\)
\(=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\therefore \cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
আবার,
\(\tan{75^{o}}=\frac{\sin{75^{o}}}{\cos{75^{o}}}\) ➜ \(\because \tan{A}=\frac{\sin{A}}{\cos{A}}\)
\(=\frac{\frac{\sqrt{3}+1}{2\sqrt{2}}}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
এবং \(\cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) ➜ লব ও হরকে \(2\sqrt{2}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \tan{75^{o}}=2+\sqrt{3}\)
বিকল্প পদ্ধতিঃ
আমরা জানি, \(\tan{75^{o}}=\tan{(45^{o}+30^{o})}\)
\(=\frac{\tan{45^{o}}+\tan{30^{o}}}{1-\tan{45^{o}}\tan{30^{o}}}\) ➜ \(\because \tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(=\frac{1+\frac{1}{\sqrt{3}}}{1-1\times\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{45^{o}}=1\)
এবং \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(=\frac{1+\frac{1}{\sqrt{3}}}{1-\frac{1}{\sqrt{3}}}\)
\(=\frac{\sqrt{3}+1}{\sqrt{3}-1}\) ➜ লব ও হরকে \(\sqrt{3}\) দ্বারা গুণ করে।
\(=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ আবার, লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{3+1+2\sqrt{3}}{3-1}\) ➜ \(\because (a+b)^2=a^2+b^2+2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4+2\sqrt{3}}{2}\)
\(=\frac{2(2+\sqrt{3})}{2}\)
\(=2+\sqrt{3}\)
\(\therefore \tan{75^{o}}=2+\sqrt{3}\)
\(\tan{75^{o}}=2+\sqrt{3}\)
আবার,
\(cosec \ {75^{o}}=\frac{1}{\sin{75^{o}}}\) ➜ \(\because cosec \ {A}=\frac{1}{\sin{A}}\)
\(=\frac{1}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\) ➜ \(\because \sin{75^{o}}=\frac{\sqrt{3}+1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}+1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}-1)}{2}\)
\(=\sqrt{2}(\sqrt{3}-1)\)
\(=\sqrt{6}-\sqrt{2}\)
\(\therefore cosec \ {75^{o}}=\sqrt{6}-\sqrt{2}\)
\(cosec \ {75^{o}}=\sqrt{6}-\sqrt{2}\)
আবার,
\(\sec{75^{o}}=\frac{1}{\cos{75^{o}}}\) ➜ \(\because \sec{A}=\frac{1}{\cos{A}}\)
\(=\frac{1}{\frac{\sqrt{3}-1}{2\sqrt{2}}}\) ➜ \(\because \cos{75^{o}}=\frac{\sqrt{3}-1}{2\sqrt{2}}\)
\(=\frac{2\sqrt{2}}{\sqrt{3}-1}\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}+1)\) দ্বারা গুণ করে।
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{3-1}\) ➜ \(\because (a+b)(a-b)=a^2-b^2\)
\(=\frac{2\sqrt{2}(\sqrt{3}+1)}{2}\)
\(=\sqrt{2}(\sqrt{3}+1)\)
\(=\sqrt{6}+\sqrt{2}\)
\(\therefore \sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
\(\sec{75^{o}}=\sqrt{6}+\sqrt{2}\)
আমরা জানি,
\(\cot{75^{o}}=\cot{(45^{o}+30^{o})}\)
\(=\frac{\cot{45^{o}}\cot{30^{o}}-1}{\cot{30^{o}}+\cot{45^{o}}}\) ➜ \(\because \cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(=\frac{1\times\sqrt{3}-1}{\sqrt{3}+1}\) ➜ \(\because \cot{45^{o}}=1\)
এবং \(\cot{30^{o}}=\sqrt{3}\)
\(=\frac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}\) ➜ লব ও হরকে \((\sqrt{3}-1)\) দ্বারা গুণ করে।
\(=\frac{3+1-2\sqrt{3}}{3-1}\) ➜ \(\because (a-b)^2=a^2+b^2-2ab\)
এবং \((a+b)(a-b)=a^2-b^2\)
\(=\frac{4-2\sqrt{3}}{2}\)
\(=\frac{2(2-\sqrt{3})}{2}\)
\(=2-\sqrt{3}\)
\(\therefore \cot{75^{o}}=2-\sqrt{3}\)
\(\cot{75^{o}}=2-\sqrt{3}\)
দ্রষ্টব্যঃ
\(15^{o}, \ 18^{o}, \ 30^{o}, \ 36^{o}\) ও \(45^{o}\) কোণের ত্রিকোণমিতিক অনুপাত জানা থাকলে নিম্নলিখিত কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় করা যায়। \(3^{o}=18^{o}-15^{o}, \ 6^{o}=36^{o}-30^{o}, \ 9^{o}=45^{o}-36^{o}, \ 12^{o}=30^{o}-18^{o}, \ 21^{o}=36^{o}-15^{o}\) ইত্যাদি।

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000002