এ অধ্যায়ের পাঠ্যসূচী
- সরলরেখার ভেক্টর সমীকরণ (Vector Equation of a Straight line)
- শর্তসাপেক্ষে সরলরেখার ভেক্টর সমীকরণ (Conditional vector equation of straight line)
- দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ (The vector equation of a straight line through two fixed points)
- সরলরেখার ভেক্টর সমীকরণ থেকে কার্তেসীয় সমীকরণ (Cartesian equation from vector equation of straight line)
- ন্যূনতম দূরত্ব (Shortest distance)
- তিনটি নির্দিষ্ট বিন্দুগামী সমতলের ভেক্টর সমীকরণ (The vector equation of a plane through three fixed points)
- একটি নির্দিষ্ট বিন্দুগামী এবং দুইটি ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ (The vector equation of a plane through a point and parallel to two vectors)
- দুইটি নির্দিষ্ট বিন্দুগামী এবং একটি ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ (The vector equation of a plane through two points which parallel to a vectors)
- একটি নির্দিষ্ট বিন্দুগামী এবং একটি ভেক্টরের উপর লম্ব সমতলের ভেক্টর সমীকরণ (The vector equation of a plane through a point which perpendicular to a vector)
- দুইটি রেখার মধ্যবর্তী ন্যূনতম দূরত্ব (Shortest distance between two vector lines)
- বাহু সাপেক্ষে সামান্তরিকের ক্ষেত্রফল (Area of Parallelogram to the side)
- ত্রিভুজের ক্ষেত্রফল (Area of Triangle)
- কর্ণ সাপেক্ষে সামান্তরিকের ক্ষেত্রফল (Area of Parallelogram to the diagonals)
- ধার সাপেক্ষে চতুস্তলকটির আয়তন (Area of Tetrahedron to the edges)
- শীর্ষবিন্দু সাপেক্ষে চতুস্তলকটির আয়তন (Area of Tetrahedron to the vertices)
- শীর্ষবিন্দু সাপেক্ষে ত্রিভুজের ক্ষেত্রফল (Area of Triangle to the vertices)
- অধ্যায় \(C\)-এর উদাহরণসমুহ
- অধ্যায় \(C\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
সরলরেখার ভেক্টর সমীকরণ
Vector Equation of a Straight line
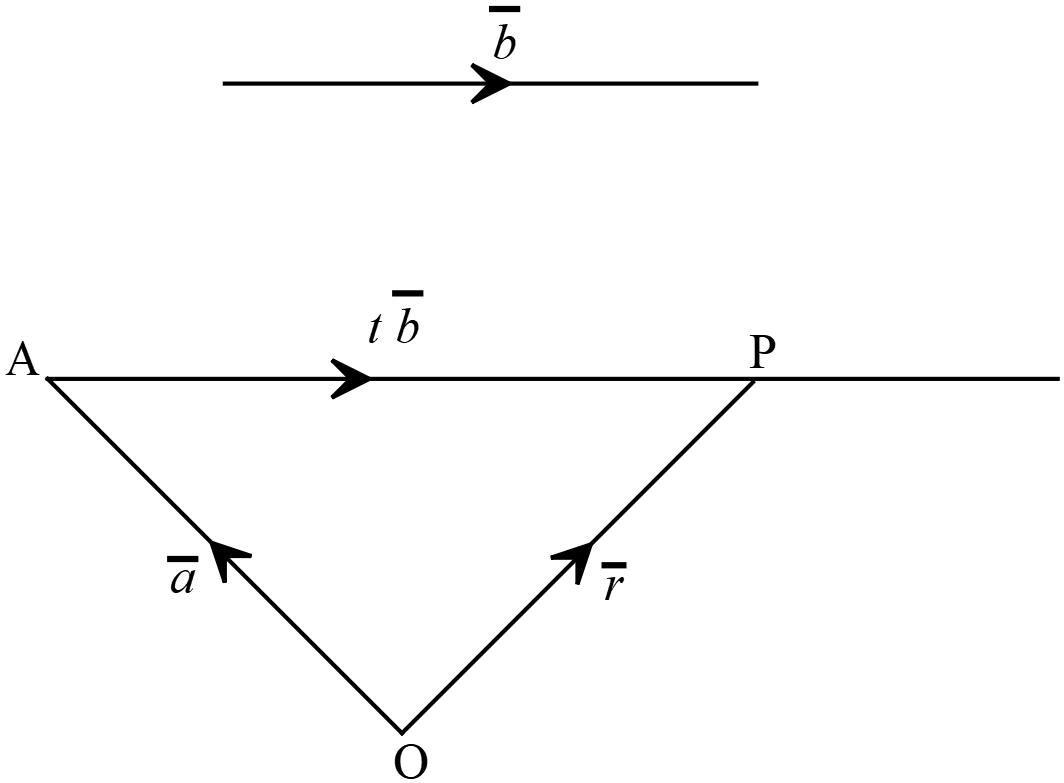\(A(\overline{a})\) বিন্দুগামী \(\overline{B}\) ভেক্টরের সমান্তরাল রেখার ভেক্টর সমীকরণঃ \(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
জাতীয়ঃ ২০১৮,২০০৮,২০০৩ ।
দ্রঃ সরলরেখাটি যদি মূলবিন্দুগামী হয় তাহলে, \(\overline{a}=\overline{0}\)
সুতরাং, মূলবিন্দুগামী এবং \(\overline{b}\) ভেক্টরের সমান্তরাল সরলরেখার ভেক্টর সমীকরণ,
\(\overline{r}=t\overline{b}\)অথবা,
\(\overline{r}\times\overline{b}=0\)
শর্তসাপেক্ষে সরলরেখার ভেক্টর সমীকরণ
Conditional vector equation of straight line
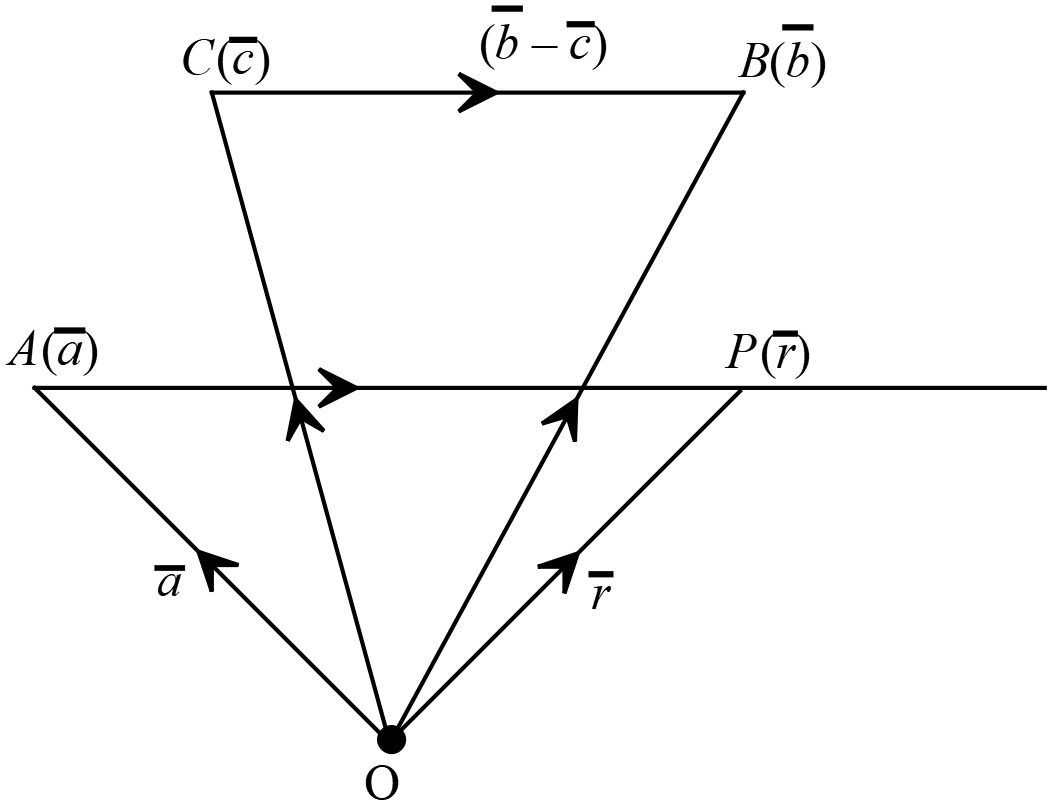\(A(\overline{a})\) বিন্দুগামী এবং \(B(\overline{b})\) ও \(C(\overline{c})\) বিন্দুদ্বয়ের সংযোগ রেখার সমান্তরাল সরলরেখার ভেক্টর সমীকরণ, \(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})=0\)
দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ
The vector equation of a straight line through two fixed points
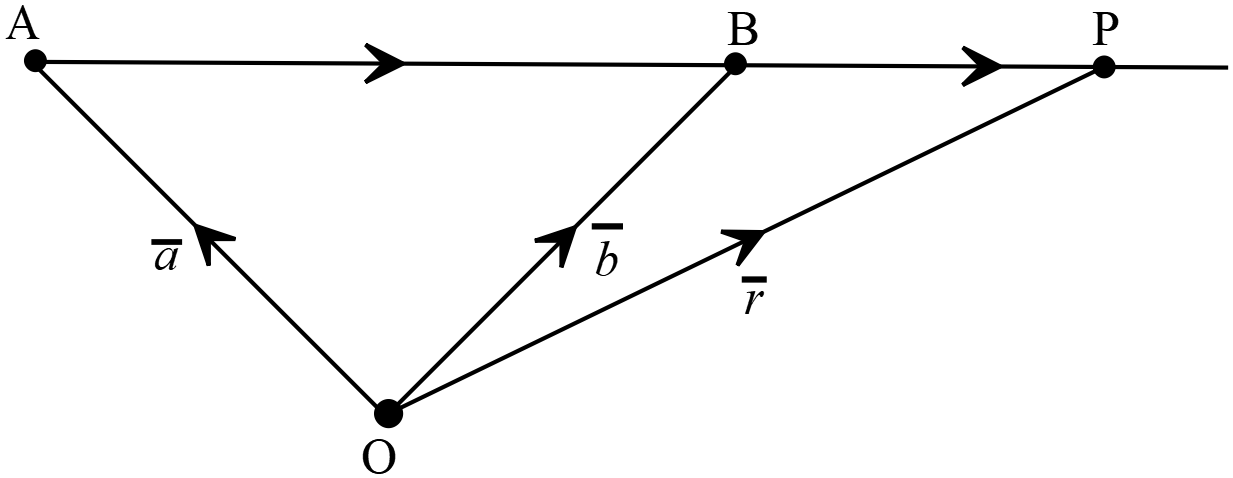\(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ,\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
সরলরেখার ভেক্টর সমীকরণ থেকে কার্তেসীয় সমীকরণ
Cartesian equation from vector equation of straight line
ভেক্টর সমীকরণ \(\overline{r}=\overline{a}+t\overline{b}\) এর কার্তেসীয় সমীকরণ,
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
ন্যূনতম দূরত্ব
Shortest distance
\(C(\overline{c})\) বিন্দু হতে \(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার ন্যূনতম দূরত্ব,
CL=\(\left|(\overline{c}-\overline{a})\times\frac{\overline{b}-\overline{a}}{|\overline{b}-\overline{a}|}\right|\)
CL=\(\left|(\overline{c}-\overline{a})\times\frac{\overline{b}-\overline{a}}{|\overline{b}-\overline{a}|}\right|\)
তিনটি নির্দিষ্ট বিন্দুগামী সমতলের ভেক্টর সমীকরণ
The vector equation of a plane through three fixed points
\(A(\overline{a}),\) \(B(\overline{b})\) এবং \(C(\overline{c})\) বিন্দুগামী সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
\([\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
একটি নির্দিষ্ট বিন্দুগামী এবং দুইটি ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ
The vector equation of a plane through a point and parallel to two vectors
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{b}\) ও \(\overline{c}\) ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{b} \ \overline{c}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
\([\overline{r} \ \overline{b} \ \overline{c}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
দুইটি নির্দিষ্ট বিন্দুগামী এবং একটি ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ
The vector equation of a plane through two points which parallel to a vectors
\(A(\overline{a})\) ও \(B(\overline{b})\) বিন্দুগামী এবং \(\overline{c}\) ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
অথবা,
\((\overline{r}-\overline{a}).\{(\overline{b}-\overline{a})\times\overline{c}\}=0\)
জাতীয়ঃ ২০০৭ ।
\([\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
অথবা,
\((\overline{r}-\overline{a}).\{(\overline{b}-\overline{a})\times\overline{c}\}=0\)
জাতীয়ঃ ২০০৭ ।
একটি নির্দিষ্ট বিন্দুগামী এবং একটি ভেক্টরের উপর লম্ব সমতলের ভেক্টর সমীকরণ
The vector equation of a plane through a point which perpendicular to a vector
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{n}\) ভেক্টরের উপর লম্ব সমতলের ভেক্টর সমীকরণ,
\(\overline{r}.\overline{n}=\overline{a}.\overline{n}\)
\(\overline{r}.\overline{n}=P\)
যেখানে, \(\overline{n}=l\hat{i}+m\hat{j}+n\hat{k}\)
\((\overline{r}-\overline{a}).\overline{n}=0\)
\((\overline{r}-\overline{a}).(\overline{n_{1}}\times\overline{n_{2}})=0\)
\((\overline{r}-\overline{a}).\{(\overline{b}-\overline{a})\times\overline{d}\}=0\)
\(\overline{r}.\overline{n}=\overline{a}.\overline{n}\)
অনুসিদ্ধান্তঃ
\(lx+my+nz=P\) সমতলের ভেক্টর সমীকরণ, \(\overline{r}.\overline{n}=P\)
যেখানে, \(\overline{n}=l\hat{i}+m\hat{j}+n\hat{k}\)
অনুসিদ্ধান্তঃ
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{r}.\overline{n}=P\) সমতলের সমান্তরাল সমতলের ভেক্টর সমীকরণ, \((\overline{r}-\overline{a}).\overline{n}=0\)
অনুসিদ্ধান্তঃ
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{r}.\overline{n_{1}}=p\) ও \(\overline{r}.\overline{n_{2}}=q\) সমতলদ্বয়ের ছেদরেখার উপর লম্ব সমতলের ভেক্টর সমীকরণ \((\overline{r}-\overline{a}).(\overline{n_{1}}\times\overline{n_{2}})=0\)
অনুসিদ্ধান্তঃ
\(A(\overline{a})\) ও \(B(\overline{b})\) বিন্দুগামী এবং \(\overline{r}=\overline{c}+t\overline{d} \) সরলরেখার সমান্তরাল সমতলের ভেক্টর সমীকরণ, \((\overline{r}-\overline{a}).\{(\overline{b}-\overline{a})\times\overline{d}\}=0\)
দুইটি রেখার মধ্যবর্তী ন্যূনতম দূরত্ব
Shortest distance between two vector lines
\(\overline{r}=\overline{a_{1}}+t\overline{b_{1}}\) ও \(\overline{r}=\overline{a_{2}}+s\overline{b_{2}}\) রেখাদ্বয়ের মধ্যবর্তী ন্যূনতম দূরত্ব,
S.D=\(\left|(\overline{a_{1}}-\overline{a_{2}}).\frac{\overline{b_{1}}\times\overline{b_{2}}}{|\overline{b_{1}}\times\overline{b_{2}}|}\right|\)
\((\overline{r}-\overline{a_{1}}).\{\overline{b_{1}}\times(\overline{b_{1}}\times\overline{b_{2}})\}=0\)
\((\overline{r}-\overline{a_{1}}).\{\overline{b_{1}}\times(\overline{b_{1}}\times\overline{b_{2}})\}=0=(\overline{r}-\overline{a_{2}}).\{\overline{b_{2}}\times(\overline{b_{1}}\times\overline{b_{2}})\}\)
S.D=\(\left|(\overline{a_{1}}-\overline{a_{2}}).\frac{\overline{b_{1}}\times\overline{b_{2}}}{|\overline{b_{1}}\times\overline{b_{2}}|}\right|\)
অনুসিদ্ধান্তঃ
\(\overline{r}=\overline{a_{1}}+t\overline{b_{1}}\) রেখা এবং ন্যূনতম দূরত্ব রেখাগামী সমতলের ভেক্টর সমীকরণ, \((\overline{r}-\overline{a_{1}}).\{\overline{b_{1}}\times(\overline{b_{1}}\times\overline{b_{2}})\}=0\)
অনুসিদ্ধান্তঃ
\(\overline{r}=\overline{a_{1}}+t\overline{b_{1}}\) রেখা এবং ন্যূনতম দূরত্ব রেখাগামী রেখার ভেক্টর সমীকরণ \((\overline{r}-\overline{a_{1}}).\{\overline{b_{1}}\times(\overline{b_{1}}\times\overline{b_{2}})\}=0=(\overline{r}-\overline{a_{2}}).\{\overline{b_{2}}\times(\overline{b_{1}}\times\overline{b_{2}})\}\)
বাহু সাপেক্ষে সামান্তরিকের ক্ষেত্রফল
Area of Parallelogram to the side
কোনো সামান্তরিকের দুইটি সন্নিহিত বাহু \(\overline{a}\) ও \(\overline{b}\) দ্বারা সূচিত হলে ঐ সামান্তরিকের ক্ষেত্রফল,
\(▱=|\overline{a}\times\overline{b}|\)
\(▱=|\overline{a}\times\overline{b}|\)
ত্রিভুজের ক্ষেত্রফল
Area of Triangle
কোনো ত্রিভুজের দুইটি বাহু \(\overline{a}\) ও \(\overline{b}\) দ্বারা সূচিত হলে ঐ ত্রিভুজের ক্ষেত্রফল,
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}|\)
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}|\)
বাহু সাপেক্ষে সামান্তরিকের ক্ষেত্রফল
Area of Parallelogram to the diagonals
\(\overline{a}\) ও \(\overline{b}\) ভেক্টর দ্বারা কোনো সামান্তরিকের দুইটি কর্ণ সূচিত হলে ঐ সামান্তরিকটির ক্ষেত্রফল,
\(▱=\frac{1}{2}|\overline{a}\times\overline{b}|\)
\(▱=\frac{1}{2}|\overline{a}\times\overline{b}|\)
ধার সাপেক্ষে চতুস্তলকটির আয়তন
Area of Tetrahedron to the edges
কোনো চতুস্তলকের সমবিন্দু ধারসমূহ \(\overline{a},\) \(\overline{b}\) ও \(\overline{c}\) ভেক্টর দ্বারা সূচিত হলে ঐ চতুস্তলকটির আয়তন,
\(\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}].\)
\(\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}].\)
শীর্ষবিন্দু সাপেক্ষে চতুস্তলকটির আয়তন
Area of Tetrahedron to the vertices
কোনো চতুস্তলকের চারটি শীর্ষবিন্দুর অবস্থান ভেক্টর \(\overline{a},\) \(\overline{b},\) \(\overline{c},\) \(\overline{d}\) হলে ঐ চতুস্তলকটির আয়তন,
\(\frac{1}{6}\{[\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}]\}.\)
\(\frac{1}{6}\{[\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}]\}.\)
শীর্ষবিন্দু সাপেক্ষে ত্রিভুজের ক্ষেত্রফল
Area of Triangle to the vertices
যদি, \(ABC\) ত্রিভুজের \(A , \ B, \ C\) শীর্ষবিন্দু সমূহের অবস্থান ভেক্টর \(\overline{a},\) \(\overline{b},\) \(\overline{c}\) হয় তবে ত্রিভুজটির ক্ষেত্রফল,
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}+\overline{b}\times\overline{c}+\overline{c}\times\overline{a}|\)
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}+\overline{b}\times\overline{c}+\overline{c}\times\overline{a}|\)
\(A(\overline{a})\) বিন্দুগামী \(\overline{B}\) ভেক্টরের সমান্তরাল রেখার ভেক্টর সমীকরণ,
\(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
জাতীয়ঃ ২০১৮,২০০৮,২০০৩ ।
প্রমাণঃ
\(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
জাতীয়ঃ ২০১৮,২০০৮,২০০৩ ।
ধরি, \(O\) মূলবিন্দু সাপেক্ষে \(A(\overline{a})\) বিন্দুর অবস্থান ভেক্টর \(\overrightarrow{OA}=\overline{a}\) এবং \(A(\overline{a})\) বিন্দুগামী সরলরেখার উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু যার \(O\) মূলবিন্দু সাপেক্ষে অবস্থান ভেক্টর \(\overrightarrow{OP}=\overline{r}\)\(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} ........(1)\)
যেহেতু, \(\overrightarrow{AP}\) ভেক্টরটি \(\overline{b}\) ভেক্টরের সমান্তরাল।
সুতরাং, \(\overrightarrow{AP}=t\overline{b},\) যখন \(t\) একটি প্যারামিটার।
\((1)\) নং হতে,
\(\overline{r}=\overline{a}+t\overline{b}\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং
\(\overrightarrow{OA}=\overline{a}\)
\(\overrightarrow{AP}=t\overline{b}\)
যা সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((1)\) নং হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overline{b}\) সমান্তরাল বলে,
\(\overrightarrow{AP}\times\overline{b}=0\)
\(\therefore (\overline{r}-\overline{a})\times\overline{b}=0\)➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
( প্রমাণিত )
\(A(\overline{a})\) বিন্দুগামী এবং \(B(\overline{b})\) ও \(C(\overline{c})\) বিন্দুদ্বয়ের সংযোগ রেখার সমান্তরাল সরলরেখার ভেক্টর সমীকরণ,
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})\)
প্রমাণঃ
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})\)
ধরি, \(O\) মূলবিন্দু সাপেক্ষে \(A(\overline{a}), B(\overline{b})\) এবং \(C(\overline{c})\) বিন্দু তিনটির অবস্থান ভেক্টর \(\overrightarrow{OA}=\overline{a}, \overrightarrow{OB}=\overline{b}\) এবং \(\overrightarrow{OC}=\overline{c}\)\(\triangle{OCB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}+\overrightarrow{CB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}\)
\(\therefore \overrightarrow{CB}=\overline{b}-\overline{c} ........(1)\)
\(A(\overline{a})\) বিন্দুগামী এবং \(CB\) রেখার সমান্তরাল সরলরেখার উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু নেই যার \(O\) মূলবিন্দু সাপেক্ষে অবস্থান ভেক্টর \(\overrightarrow{OP}=\overline{r}\)
\(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} ........(2)\)
যেহেতু, \(\overrightarrow{AP}\) ভেক্টরটি \(\overrightarrow{CB}=\overline{b}-\overline{c}\) ভেক্টরের সমান্তরাল।
সুতরাং, \(\overrightarrow{AP}=t\overrightarrow{CB}\) যখন \(t\) একটি প্যারামিটার।
\(\therefore \overrightarrow{AP}=t(\overline{b}-\overline{c})\)
\((2)\) নং হতে,
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
\(\overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AP}=t(\overline{b}-\overline{c})\)
যা সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((2)\) নং হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AP}=\overline{r}-\overline{a} ......(3)\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overrightarrow{CB}\) সমান্তরাল বলে,
\(\overrightarrow{AP}\times\overrightarrow{CB}=0\)
\((3)\) ও \((1)\) নং হতে,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{c})=0\)
( প্রমাণিত )
\(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ,
\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
প্রমাণঃ
\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
ধরি, \(O\) মূলবিন্দু , \(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দু দিয়ে যায় এবং রেখাটির উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু \(O\) মূলবিন্দু সাপেক্ষে \(A, B\) এবং \(P\) বিন্দুগুলির অবস্থান ভেক্টর যথাক্রমে \(\overrightarrow{OA}=\overline{a}, \overrightarrow{OB}=\overline{b}\) এবং \(\overrightarrow{OP}=\overline{r}\)
\(\triangle{OAB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AB}=\overline{b}-\overline{a} ........(1)\) ➜ \(\because \overrightarrow{OB}=\overline{b}\)
এবং
\(\overrightarrow{OA}=\overline{a}\)
যেহেতু, \(\overrightarrow{AP}\) এবং \(\overrightarrow{AB}\) ভেক্টরদ্বয় একই ধারক রেখার উপর অবস্থিত।
সুতরাং, \(\overrightarrow{AP}=t\overrightarrow{AB}\) যখন \(t\) একটি প্যারামিটার।
\(\therefore \overrightarrow{AP}=t(\overline{b}-\overline{a}) .......(2)\)
আবার, \(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} .......(3)\)
\((3)\) হতে,
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{a})\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
\(\overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AP}=t(\overline{b}-\overline{a})\)
\(\Rightarrow \overline{r}=\overline{a}+t\overline{b}-t\overline{a}\)
\(\therefore \overline{r}=(1-t)\overline{a}+t\overline{b}\)
যা দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((3)\) হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{AP}=\overline{r}-\overline{a} ......(4)\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overrightarrow{AB}\) একই সরলরেখায় অবস্থিত বলে,
\(\overrightarrow{AP}\times\overrightarrow{AB}=0\)
\((4)\) ও \((1)\) নং হতে,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
( প্রমাণিত )
\(C(\overline{c})\) বিন্দু হতে \(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার ন্যূনতম দূরত্ব,
CL=\(\left|(\overline{c}-\overline{a})\times\frac{\overline{b}-\overline{a}}{|\overline{b}-\overline{a}|}\right|\)
প্রমাণঃ
CL=\(\left|(\overline{c}-\overline{a})\times\frac{\overline{b}-\overline{a}}{|\overline{b}-\overline{a}|}\right|\)
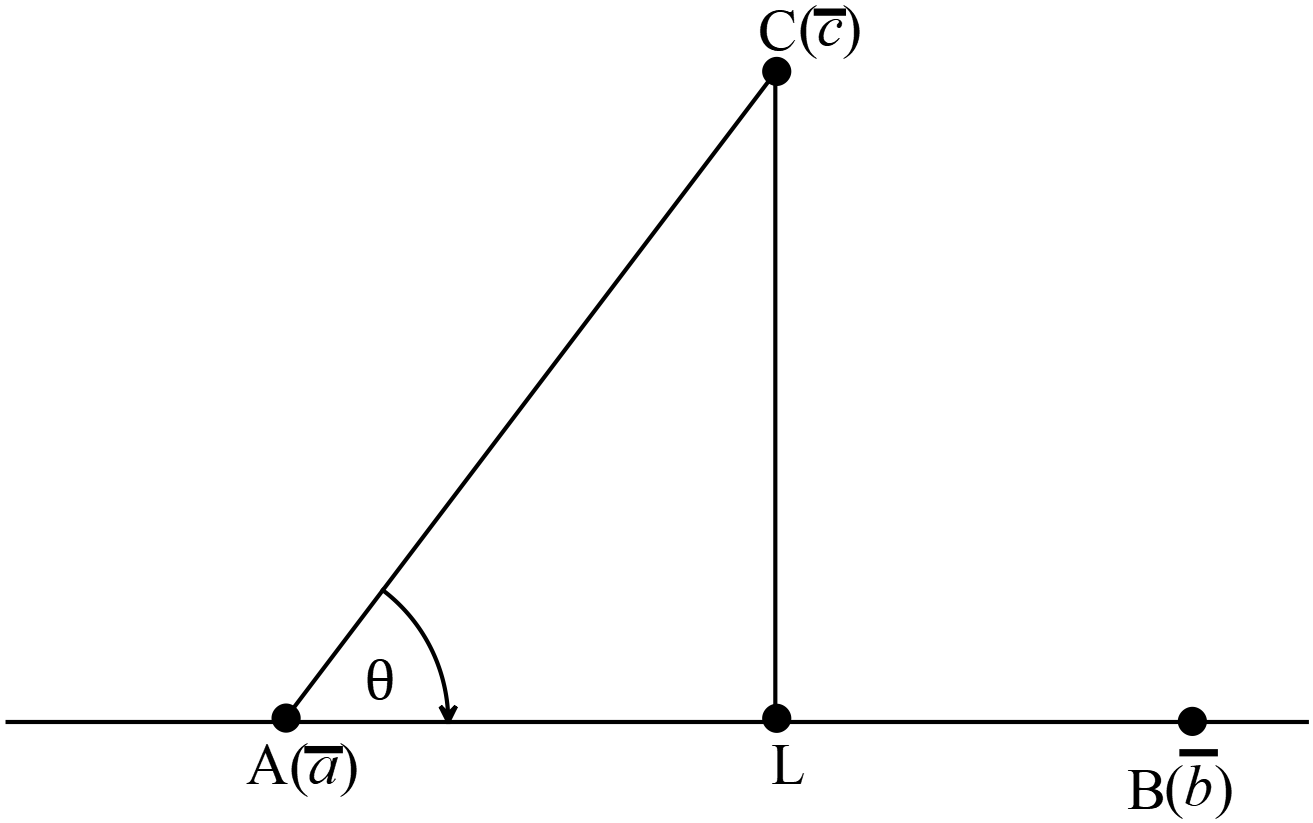ধরি,\(C(\overline{c})\) বিন্দু হতে \(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার ন্যূনতম দূরত্ব \(CL\) এবং \(\angle{CAL}=\theta.\)
এখন, \(\overrightarrow{AB}=\overline{b}-\overline{a}\) ➜ \(\because P(\overline{p})\) এবং \(Q(\overline{q})\) হলে,
\(\overrightarrow{PQ}=\overline{q}-\overline{p}\) হয়।
\(\Rightarrow AB=|\overrightarrow{AB}|\)
\(\therefore AB=|\overline{b}-\overline{a}|\)
\(\triangle{ACL}\) হতে,
\(\sin{\theta}=\frac{CL}{AC}\)
\(\Rightarrow CL=AC\sin{\theta}\)
\(\Rightarrow CL=AC\frac{|\overrightarrow{AC}\times\overrightarrow{AB}|}{|\overrightarrow{AC}||\overrightarrow{AB}|}\) ➜ \(\because \sin{\theta}=\frac{|\overrightarrow{AC}\times\overrightarrow{AB}|}{|\overrightarrow{AC}||\overrightarrow{AB}|}\)
\(\Rightarrow CL=AC\frac{|\overrightarrow{AC}\times\overrightarrow{AB}|}{AC \ AB}\) ➜ \(\because |\overrightarrow{AC}|=AC\)
এবং \(|\overrightarrow{AB}|=AB\)
\(\Rightarrow CL=\frac{|\overrightarrow{AC}\times\overrightarrow{AB}|}{AB}\)
\(\Rightarrow CL=\left|\overrightarrow{AC}\times\frac{\overrightarrow{AB}}{AB}\right|\)
\(\therefore CL=\left|\overrightarrow{AC}\times\frac{\overline{b}-\overline{a}}{|\overline{b}-\overline{a}|}\right|\) ➜ \(\because \overrightarrow{AB}=\overline{b}-\overline{a}\)
এবং \(AB=|\overline{b}-\overline{a}|\)
( প্রমাণিত )
\(A(\overline{a}),\) \(B(\overline{b})\) এবং \(C(\overline{c})\) বিন্দুগামী সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
প্রমাণঃ
\([\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
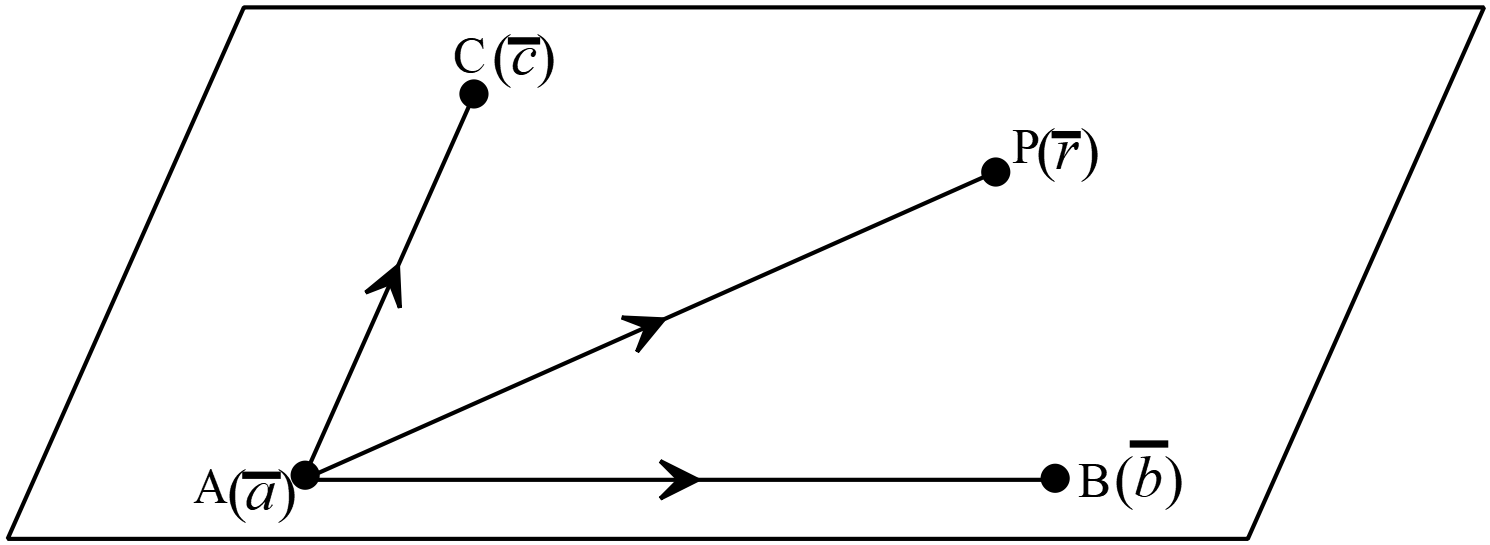ধরি,\(A(\overline{a}),\) \(B(\overline{b})\) এবং \(C(\overline{c})\) বিন্দুগামী সমতলের উপরস্থ যে কোনো বিন্দু \(P(\overline{r}).\)
এখন, \(\overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
অনুরূপভাবে, \(\overrightarrow{AB}=\overline{b}-\overline{a}\)
\(\overrightarrow{AC}=\overline{c}-\overline{a}\)
যেহেতু, \(A(\overline{a}),\) \(B(\overline{b}),\) \(C(\overline{c}),\) \(P(\overline{r})\) বিন্দুসমূহ একই সমতলে অবস্থিত,
সুতরাং, \(\overrightarrow{AP},\) \(\overrightarrow{AB}\) এবং \(\overrightarrow{AC}\) ভেক্টরসমূহ একই সমতলে থাকবে।
\([\overrightarrow{AP} \ \overrightarrow{AB} \ \overrightarrow{AC}]=0\) ➜ \(\overrightarrow{PQ},\) \(\overrightarrow{QR}\) এবং \(\overrightarrow{PR}\) ভেক্টরত্রয়ের একই সমতলে অবস্থান করার শর্ত,
\([\overrightarrow{PQ} \ \overrightarrow{QR} \ \overrightarrow{PR}]=0\)
\(\Rightarrow \overrightarrow{AP}.(\overrightarrow{AB}\times\overrightarrow{AC})=0\) ➜ \(\because [\overline{p} \ \overline{q} \ \overline{r}]=\overline{p}.(\overline{q}\times\overline{r})\)
\(\Rightarrow (\overline{r}-\overline{a}).\{(\overline{b}-\overline{a})\times(\overline{c}-\overline{a})\}=0\) ➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
\(\overrightarrow{AB}=\overline{b}-\overline{a}\)
এবং \(\overrightarrow{AC}=\overline{c}-\overline{a}\)
\(\Rightarrow (\overline{r}-\overline{a}).\{\overline{b}\times\overline{c}-\overline{b}\times\overline{a}-\overline{a}\times\overline{c}+\overline{a}\times\overline{a}\}=0\)
\(\Rightarrow (\overline{r}-\overline{a}).\{\overline{b}\times\overline{c}+\overline{a}\times\overline{b}+\overline{c}\times\overline{a}+0\}=0\) ➜ \(\because \overline{b}\times\overline{a}=-\overline{a}\times\overline{b}\)
\(\overline{a}\times\overline{c}=-\overline{c}\times\overline{a}\)
এবং \(\overline{a}\times\overline{a}=0\)
\(\Rightarrow (\overline{r}-\overline{a}).\{\overline{b}\times\overline{c}+\overline{a}\times\overline{b}+\overline{c}\times\overline{a}\}=0\)
\(\Rightarrow \overline{r}.(\overline{b}\times\overline{c})+\overline{r}.(\overline{a}\times\overline{b})+\overline{r}.(\overline{c}\times\overline{a})-\overline{a}.(\overline{b}\times\overline{c})-\overline{a}.(\overline{a}\times\overline{b})-\overline{a}.(\overline{c}\times\overline{a})=0\)
\(\Rightarrow [\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{c} \ \overline{a}]-[\overline{a} \ \overline{b} \ \overline{c}]-0-0=0\) ➜ \(\because \overline{r}.(\overline{b}\times\overline{c})= [\overline{r} \ \overline{b} \ \overline{c}]\)
\(\overline{r}.(\overline{a}\times\overline{b})=[\overline{r} \ \overline{a} \ \overline{b}]\)
\(\overline{r}.(\overline{c}\times\overline{a})=[\overline{r} \ \overline{c} \ \overline{a}]\)
\(\overline{a}.(\overline{b}\times\overline{c})=[\overline{a} \ \overline{b} \ \overline{c}]\)
\(\overline{a}.(\overline{a}\times\overline{b})=0\)
এবং \(\overline{a}.(\overline{c}\times\overline{a})=0\)
\(\Rightarrow [\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{c} \ \overline{a}]-[\overline{a} \ \overline{b} \ \overline{c}]=0\)
\(\therefore [\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{a} \ \overline{b}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
( প্রমাণিত )
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{b}\) ও \(\overline{c}\) ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{b} \ \overline{c}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
প্রমাণঃ
\([\overline{r} \ \overline{b} \ \overline{c}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
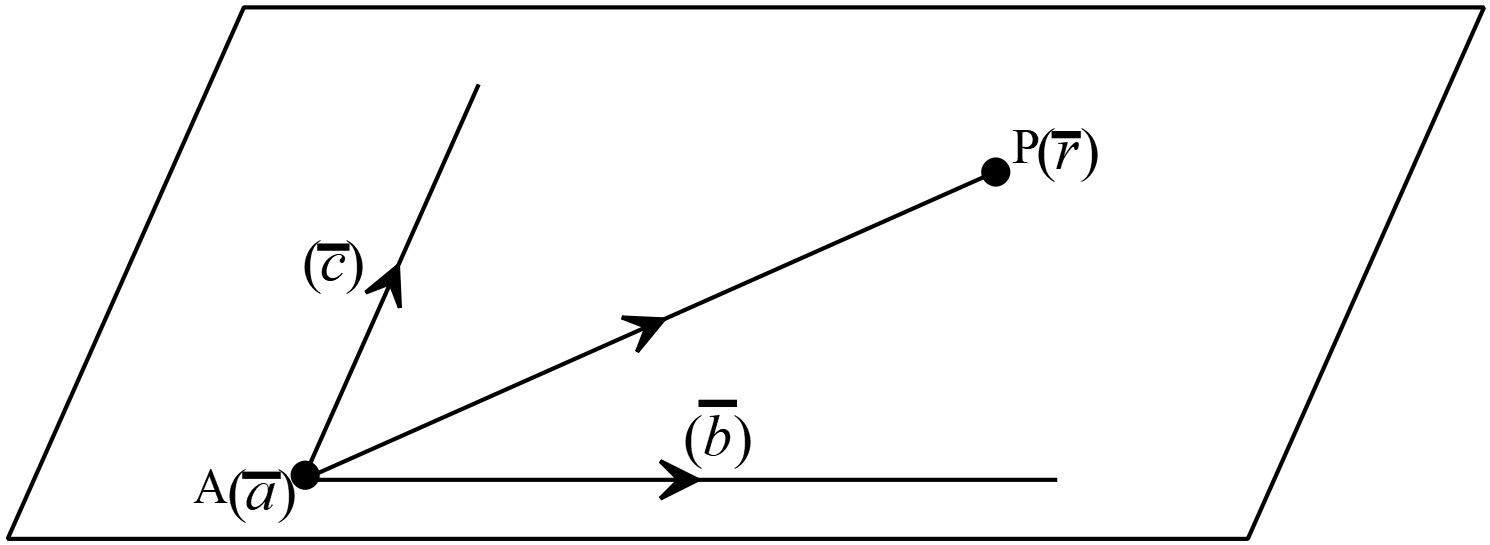ধরি,\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{b}\) ও \(\overline{c}\) ভেক্টরের সমান্তরাল সমতলের উপরস্থ যে কোনো বিন্দু \(P(\overline{r}).\)
এখন, \(\overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
শর্তমতে, \(\overrightarrow{AP}\) ভেক্টর সমতলে থাকবে এবং \(\overline{b}\times\overline{c}\) ভেক্টরের সহিত লম্ব হবে।
\(\overrightarrow{AP}.(\overline{b}\times\overline{c})=0\) ➜ \(\overrightarrow{PQ}\) এবং \(\overrightarrow{QR}\) ভেক্টরদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত,
\(\overrightarrow{PQ}.\overrightarrow{QR}=0\)
\(\Rightarrow (\overline{r}-\overline{a}).(\overline{b}\times\overline{c})=0\) ➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
\(\Rightarrow \overline{r}.(\overline{b}\times\overline{c})-\overline{a}.(\overline{b}\times\overline{c})=0\)
\(\Rightarrow [\overline{r} \ \overline{b} \ \overline{c}]-[\overline{a} \ \overline{b} \ \overline{c}]=0\) ➜ \(\because \overline{r}.(\overline{b}\times\overline{c})= [\overline{r} \ \overline{b} \ \overline{c}]\)
এবং \(\overline{a}.(\overline{b}\times\overline{c})=[\overline{a} \ \overline{b} \ \overline{c}]\)
\(\therefore [\overline{r} \ \overline{b} \ \overline{c}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
( প্রমাণিত )
\(A(\overline{a})\) ও \(B(\overline{b})\) বিন্দুগামী এবং \(\overline{c}\) ভেক্টরের সমান্তরাল সমতলের ভেক্টর সমীকরণ,
\([\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
জাতীয়ঃ ২০০৭ ।
প্রমাণঃ
\([\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]\)
জাতীয়ঃ ২০০৭ ।
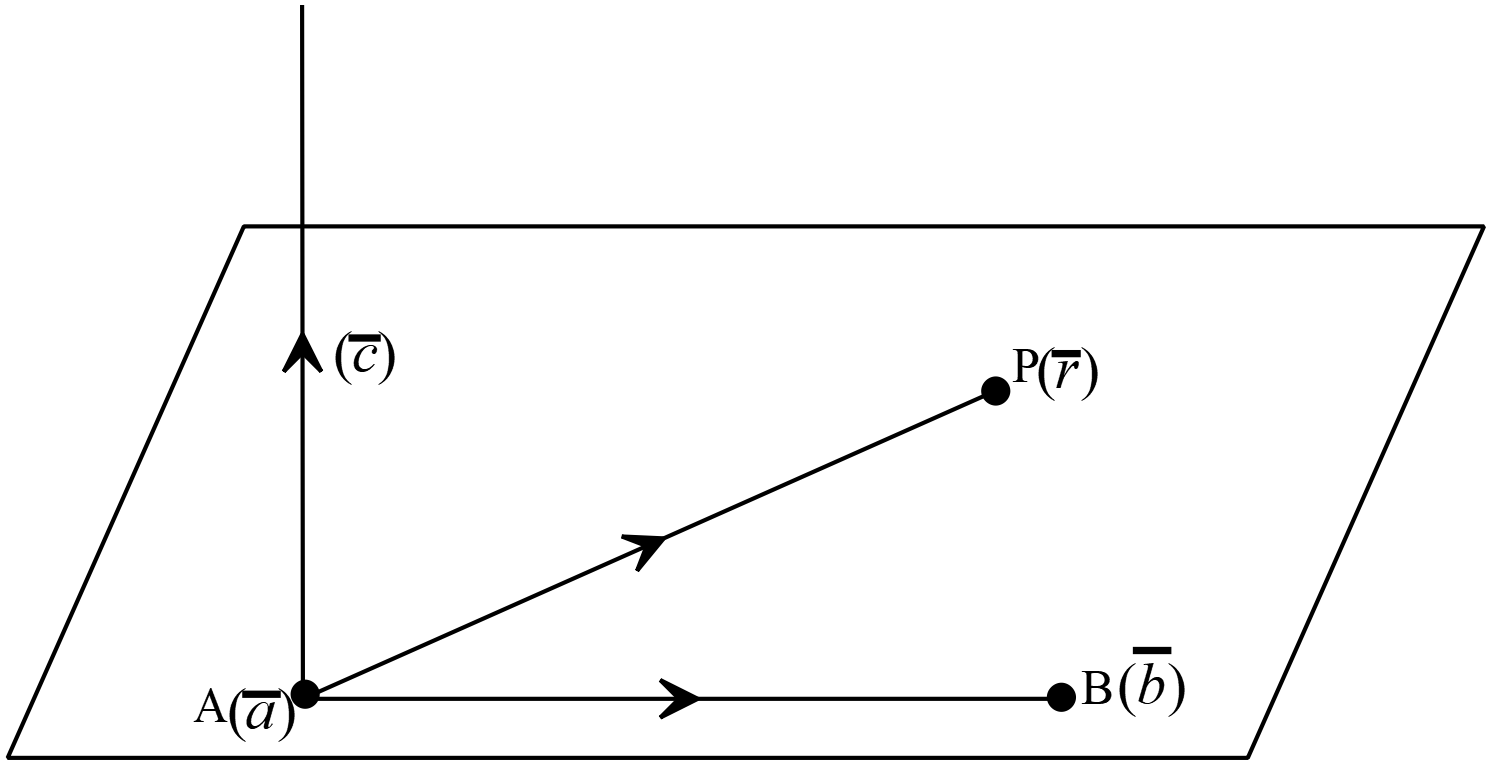ধরি,\(A(\overline{a})\) ও \(B(\overline{b})\)
এখন, \(\overrightarrow{AB}=\overline{b}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
সমতলের উপরস্থ যে কোনো বিন্দু \(P(\overline{r}).\)
\(\therefore \overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
যেহেতু সমতলটি \(\overline{c}\) ভেক্টরের সমান্তরাল,
সুতরাং, \(\overline{c}\) ভেক্টরটি \(\overrightarrow{AP}\times\overrightarrow{AB}\) এর সহিত লম্ব হবে,
অর্থাৎ, \(\overline{c}.(\overrightarrow{AP}\times\overrightarrow{AB})=0\) হবে, ➜ \(\overrightarrow{PQ}\) এবং \(\overrightarrow{QR}\) ভেক্টরদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত,
\(\overrightarrow{PQ}.\overrightarrow{QR}=0\)
\(\Rightarrow \overline{c}.\{(\overline{r}-\overline{a})\times(\overline{b}-\overline{a})\}=0\) ➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
এবং \(\overrightarrow{AB}=\overline{b}-\overline{a}\)
\(\Rightarrow \overline{c}.\{\overline{r}\times\overline{b}-\overline{r}\times\overline{a}-\overline{a}\times\overline{b}+\overline{a}\times\overline{a}\}=0\)
\(\Rightarrow \overline{c}.(\overline{r}\times\overline{b})-\overline{c}.(\overline{r}\times\overline{a})-\overline{c}.(\overline{a}\times\overline{b})+0=0\) ➜ \(\because \overline{a}\times\overline{a}=0\)
\(\Rightarrow [\overline{c} \ \overline{r} \ \overline{b}]-[\overline{c} \ \overline{r} \ \overline{a}]-[\overline{c} \ \overline{a} \ \overline{b}]=0\) ➜ \(\because \overline{c}.(\overline{r}\times\overline{b})=[\overline{c} \ \overline{r} \ \overline{b}]\)
\(\overline{c}.(\overline{r}\times\overline{a})=[\overline{c} \ \overline{r} \ \overline{a}]\)
এবং \(\overline{c}.(\overline{a}\times\overline{b})=[\overline{c} \ \overline{a} \ \overline{b}]\)
\(\Rightarrow [\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]-[\overline{a} \ \overline{b} \ \overline{c}]=0\) ➜ \(\because [\overline{c} \ \overline{r} \ \overline{b}]=[\overline{r} \ \overline{b} \ \overline{c}]\)
\([\overline{c} \ \overline{r} \ \overline{a}]=-[\overline{r} \ \overline{c} \ \overline{a}]\)
এবং \(\overline{c}.(\overline{a}\times\overline{b})=[\overline{a} \ \overline{b} \ \overline{c}]\)
\(\therefore [\overline{r} \ \overline{b} \ \overline{c}]+[\overline{r} \ \overline{c} \ \overline{a}]=[\overline{a} \ \overline{b} \ \overline{c}]=0\)
( প্রমাণিত )
\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{n}\) ভেক্টরের উপর লম্ব সমতলের ভেক্টর সমীকরণ,
\(\overline{r}.\overline{n}=\overline{a}.\overline{n}\)
প্রমাণঃ
\(\overline{r}.\overline{n}=\overline{a}.\overline{n}\)
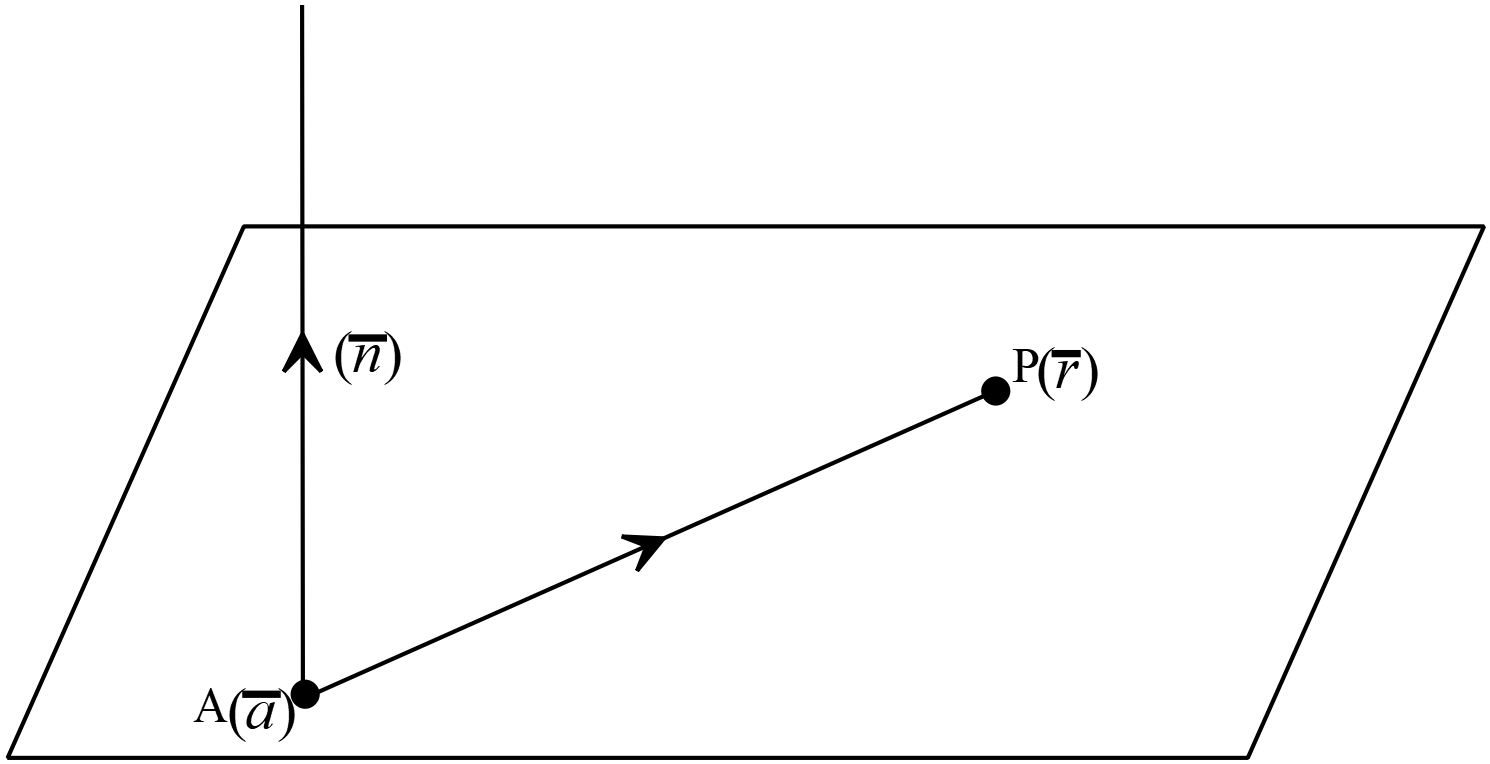ধরি,\(A(\overline{a})\) বিন্দুগামী এবং \(\overline{n}\) ভেক্টরের উপর লম্ব সমতলের উপরস্থ যে কোনো বিন্দু \(P(\overline{r}).\)
এখন, \(\overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
তাহলে, \(\overrightarrow{AP}\) ভেক্টর সমতলে থাকবে এবং \(\overline{n}\) ভেক্টরের উপর লম্ব হবে।
সুতরাং, \(\overrightarrow{AP}.\overline{n}=0\) হবে
\(\Rightarrow (\overline{r}-\overline{a}).\overline{n}=0\) ➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
\(\Rightarrow \overline{r}.\overline{n}-\overline{a}.\overline{n}=0\)
\(\therefore \overline{r}.\overline{n}=\overline{a}.\overline{n}\)
( প্রমাণিত )
\(\overline{r}=\overline{a_{1}}+t\overline{b_{1}} \) ও \(\overline{r}=\overline{a_{2}}+t\overline{b_{2}} \) রেখাদ্বয়ের মধ্যবর্তী ন্যূনতম দূরত্ব,
S.D=\(\left|(\overline{a_{1}}-\overline{a_{2}}).\frac{\overline{b_{1}}\times\overline{b_{2}}}{|\overline{b_{1}}\times\overline{b_{2}}|}\right|\)
প্রমাণঃ
S.D=\(\left|(\overline{a_{1}}-\overline{a_{2}}).\frac{\overline{b_{1}}\times\overline{b_{2}}}{|\overline{b_{1}}\times\overline{b_{2}}|}\right|\)
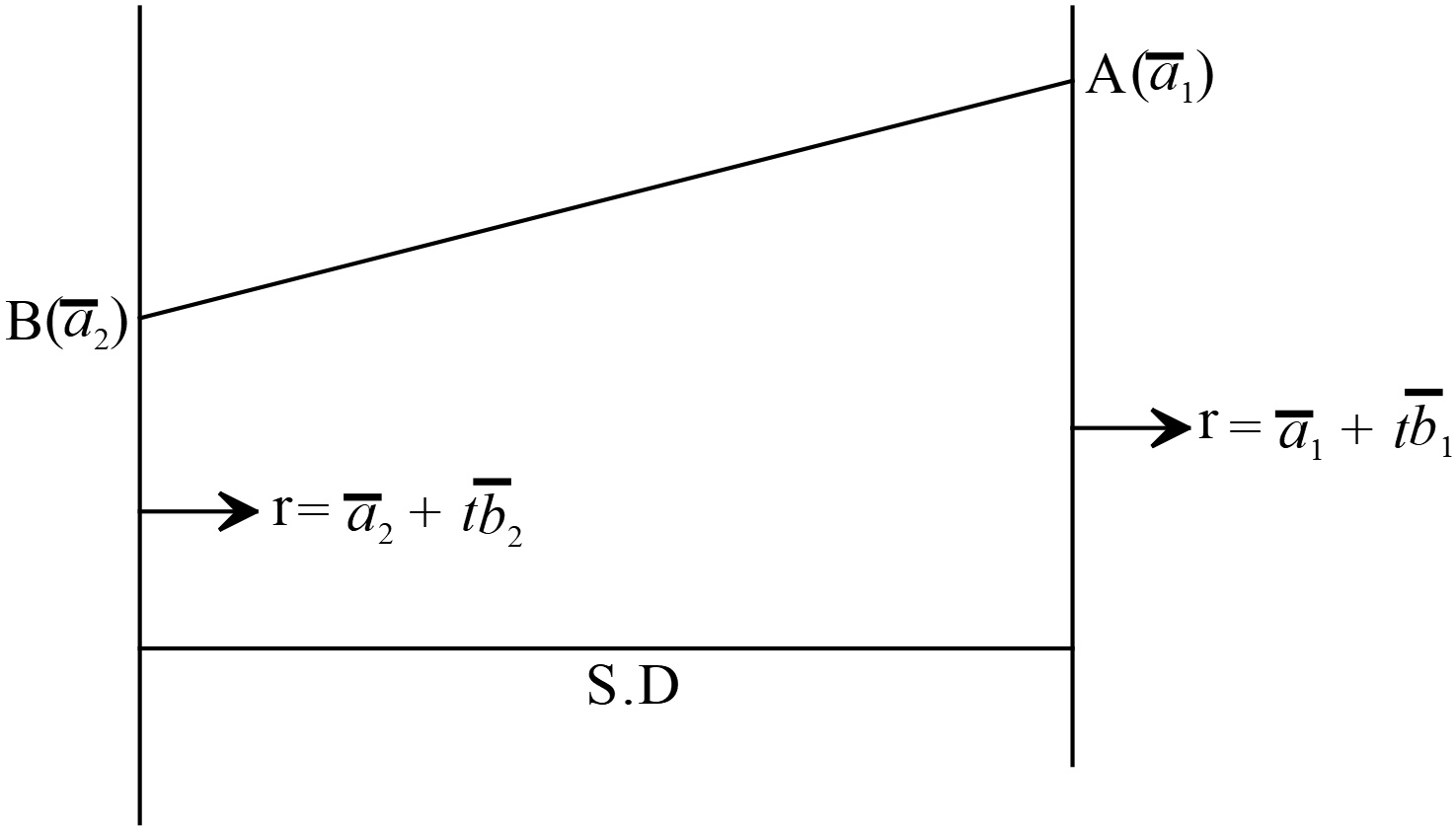লম্বদূরত্ব (S.D),\(\overline{r}=\overline{a_{1}}+t\overline{b_{1}} \) ও \(\overline{r}=\overline{a_{2}}+t\overline{b_{2}} \) রেখাদ্বয়ের উভয়ের সহিত লম্ব।
সুতরাং ন্যূনতম দূরত্ব \(\overline{b_{1}}\times\overline{b_{2}}\) ভেক্টরের সহিত সমান্তরাল হবে।
\(\therefore S.D=\) | ন্যূনতম দূরত্ব রেখা বরাবর \(BA\) রেখার লম্ব অভিক্ষেপ | যেখানে, \(B(\overline{a_{2}})\) ও \(A(\overline{a_{1}})\)
\(=\) | \(\overline{b_{1}}\times\overline{b_{2}}\) বরাবর \((\overline{a_{1}}-\overline{a_{2}})\) ভেক্টরের লম্ব অভিক্ষেপ |
\(=\left|(\overline{a_{1}}-\overline{a_{2}}).\frac{\overline{b_{1}}\times\overline{b_{2}}}{|\overline{b_{1}}\times\overline{b_{2}}|}\right|\) ➜ \(\because \overline{m}, \ \overline{n}\) হলে,
\(\overline{m}\) বরাবর \(\overline{n}\) এর লম্ব অভিক্ষেপ,
\(=\overline{n}.\frac{\overline{m}}{|\overline{m}|}\)
( প্রমাণিত )
কোনো সামান্তরিকের দুইটি সন্নিহিত বাহু \(\overline{a}\) ও \(\overline{b}\) দ্বারা সূচিত হলে ঐ সামান্তরিকের ক্ষেত্রফল,
\(▱=|\overline{a}\times\overline{b}|\)
প্রমাণঃ
\(▱=|\overline{a}\times\overline{b}|\)
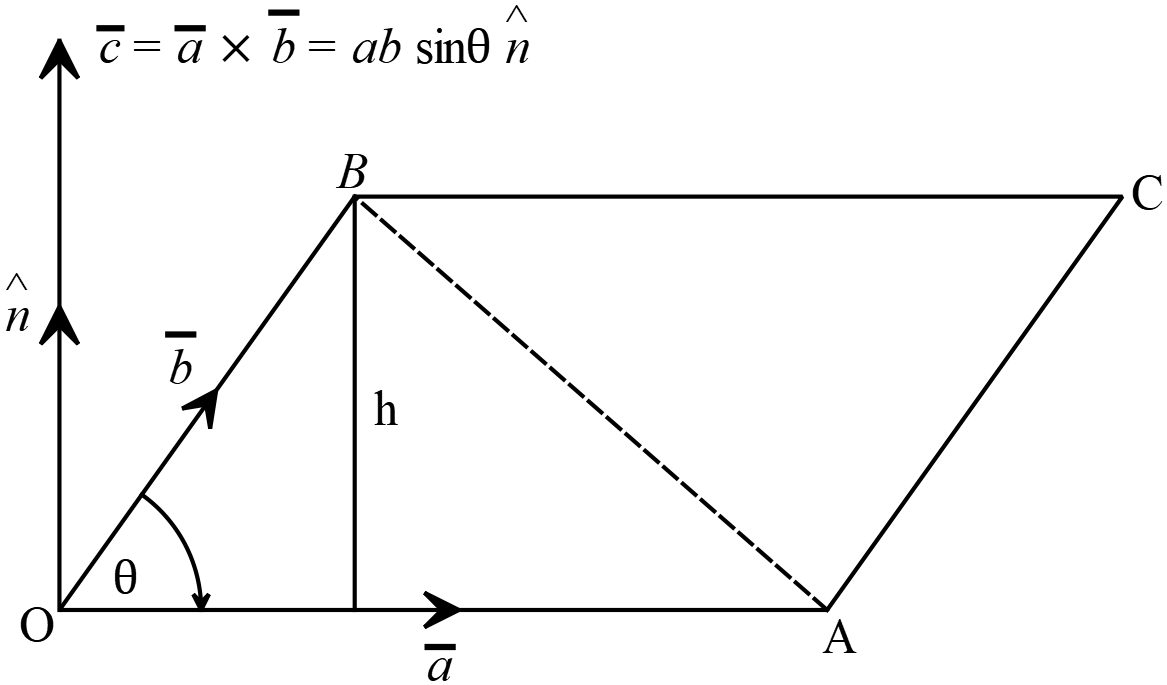\(OACB\) সামান্তরিকের \(OA\) এবং \(OB\) সন্নিহিত বাহু দুইটি দ্বারা যথাক্রমে \(\overline{a}\) এবং \(\overline{b}\) ভেক্টর দুইটি সূচীত করা হলো। যদি \(\angle{AOB}=\theta\) হয়,
তাহলে, \(\overline{a}\times{\overline{b}}=\overrightarrow{OA}\times{\overrightarrow{OB}}\)
\(=OA \ OB \sin{\theta} \ \hat{n}\)
\(=ab\sin{\theta} \ \hat{n}\)
\(=\overline{c}\)
যেখানে, \(\hat{n}\) হলো \(\overline{a}\) এবং \(\overline{b}\) ভেক্টরদ্বয়ের সমতলের উপর লম্ব একক ভেক্টর। উল্লেখ্য, ডানহাতি স্ক্র \(\overline{a}\) থেকে \(\overline{b}\) এর দিকে ক্ষুদ্রতম কোণে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(OD\) বরাবর এবং \(\overline{b}\) থেকে \(\overline{a}\) এর দিকে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(DO\) বরাবর হবে।
\(\overline{a}\times{\overline{b}}=OA \ OB \sin{\theta}\)
\(=OA \ h\) যখন, \(h=OB \sin{\theta}\)
\(=OACB\) সামান্তরিকের ক্ষেত্রফল।
\(▱OACB=|\overline{a}\times{\overline{b}}|\)
( প্রমাণিত )
কোনো ত্রিভুজের দুইটি বাহু \(\overline{a}\) ও \(\overline{b}\) দ্বারা সূচিত হলে ঐ ত্রিভুজের ক্ষেত্রফল,
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}|\)
প্রমাণঃ
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}|\)
\(OACB\) সামান্তরিকের \(OA\) এবং \(OB\) সন্নিহিত বাহু দুইটি দ্বারা যথাক্রমে \(\overline{a}\) এবং \(\overline{b}\) ভেক্টর দুইটি সূচীত করা হলো। যদি \(\angle{AOB}=\theta\) হয়,
তাহলে, \(\overline{a}\times{\overline{b}}=\overrightarrow{OA}\times{\overrightarrow{OB}}\)
\(=OA \ OB \sin{\theta} \ \hat{n}\)
\(=ab\sin{\theta} \ \hat{n}\)
\(=\overline{c}\)
যেখানে, \(\hat{n}\) হলো \(\overline{a}\) এবং \(\overline{b}\) ভেক্টরদ্বয়ের সমতলের উপর লম্ব একক ভেক্টর। উল্লেখ্য, ডানহাতি স্ক্র \(\overline{a}\) থেকে \(\overline{b}\) এর দিকে ক্ষুদ্রতম কোণে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(OD\) বরাবর এবং \(\overline{b}\) থেকে \(\overline{a}\) এর দিকে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(DO\) বরাবর হবে।
\(\overline{a}\times{\overline{b}}=OA \ OB \sin{\theta}\)
\(=OA \ h\) যখন, \(h=OB \sin{\theta}\)
\(=OACB\) সামান্তরিকের ক্ষেত্রফল।
আবার, \(\frac{1}{2}|\overline{a}\times{\overline{b}}|=\frac{1}{2}.OA.h\)
\(=\triangle{OAB}\)
\(\triangle{OAB}=\frac{1}{2}|\overline{a}\times{\overline{b}}|\)
( প্রমাণিত )
\(\overline{a}\) ও \(\overline{b}\) ভেক্টর দ্বারা কোনো সামান্তরিকের দুইটি কর্ণ সূচিত হলে ঐ সামান্তরিকটির ক্ষেত্রফল,
\(▱=\frac{1}{2}|\overline{a}\times\overline{b}|\)
প্রমাণঃ
\(▱=\frac{1}{2}|\overline{a}\times\overline{b}|\)
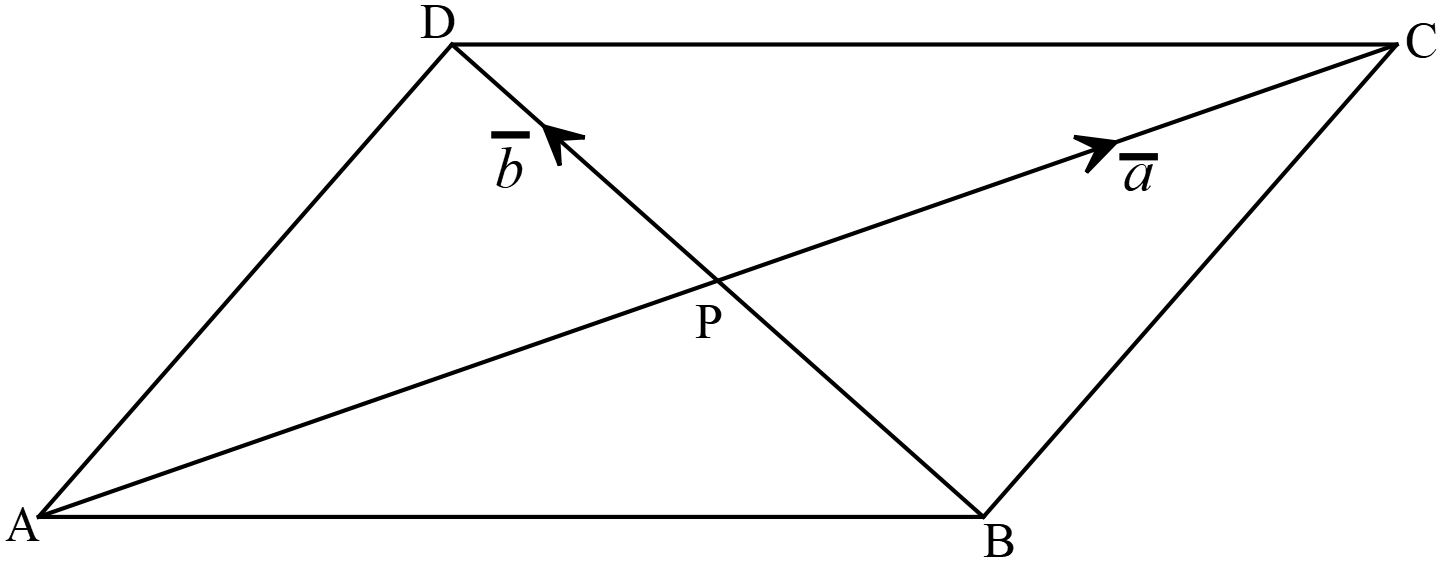যদি, \(ABCD\) সামান্তরিকের \(AC\) এবং \(BD\) কর্ণদ্বয় পরস্পর \(P\) বিন্দুতে ছেদ করে।
\(\overrightarrow{AC}=\overline{a}\) এবং \(\overrightarrow{BD}=\overline{b}\) হয় তবে,
\(\overrightarrow{PC}=\frac{1}{2}\overrightarrow{AC}=\frac{1}{2}\overline{a}\)
এবং \(\overrightarrow{PD}=\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}\overline{b}\)
এখন, \(\triangle{PCD}\) এর ক্ষেত্রফল,
\(=\frac{1}{2}|\overrightarrow{PC}\times\overrightarrow{PD}|\)
\(=\frac{1}{2}|\frac{1}{2}\overline{a}\times\frac{1}{2}\overline{b}|\) ➜ \(\because \overrightarrow{PC}=\frac{1}{2}\overline{a}\)
এবং \(\overrightarrow{PD}=\frac{1}{2}\overline{b}\)
\(=\frac{1}{2}|\frac{1}{4}\overline{a}\times\overline{b}|\)
\(\therefore \triangle{PCD}=\frac{1}{8}|\overline{a}\times\overline{b}|\)
আবার, \(▱ABCD=4\times\triangle{PCD}\)
\(=4\times\frac{1}{8}|\overline{a}\times\overline{b}|\) ➜ \(\because \triangle{PCD}=\frac{1}{8}|\overline{a}\times\overline{b}|\)
\(=\frac{1}{2}|\overline{a}\times\overline{b}|\)
\(\therefore ▱ABCD=\frac{1}{2}|\overline{a}\times\overline{b}|\)
\(▱=\frac{1}{2}|\overline{a}\times\overline{b}|\)
( প্রমাণিত )
কোনো চতুস্তলকের সমবিন্দু ধারসমূহ \(\overline{a},\) \(\overline{b}\) ও \(\overline{c}\) ভেক্টর দ্বারা সূচিত হলে ঐ চতুস্তলকটির আয়তন,
\(\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}].\)
প্রমাণঃ
\(\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}].\)
স্কেলার ট্রিপল প্রডাক্ট এর জ্যামিতিক ব্যাখ্যা হতে জানি,
কোনো সামান্তরিক আকারের ঘনবস্তুর সমবিন্দু ধারসমূহ \(\overline{a}, \ \overline{b}\) এবং \(\overline{c}\) দ্বারা সূচিত হলে \([\overline{a} \ \overline{b} \ \overline{c}]\) দ্বারা ঐ সামান্তরিক আকারের ঘনবস্তুর আয়তন নির্দেশিত হয়।
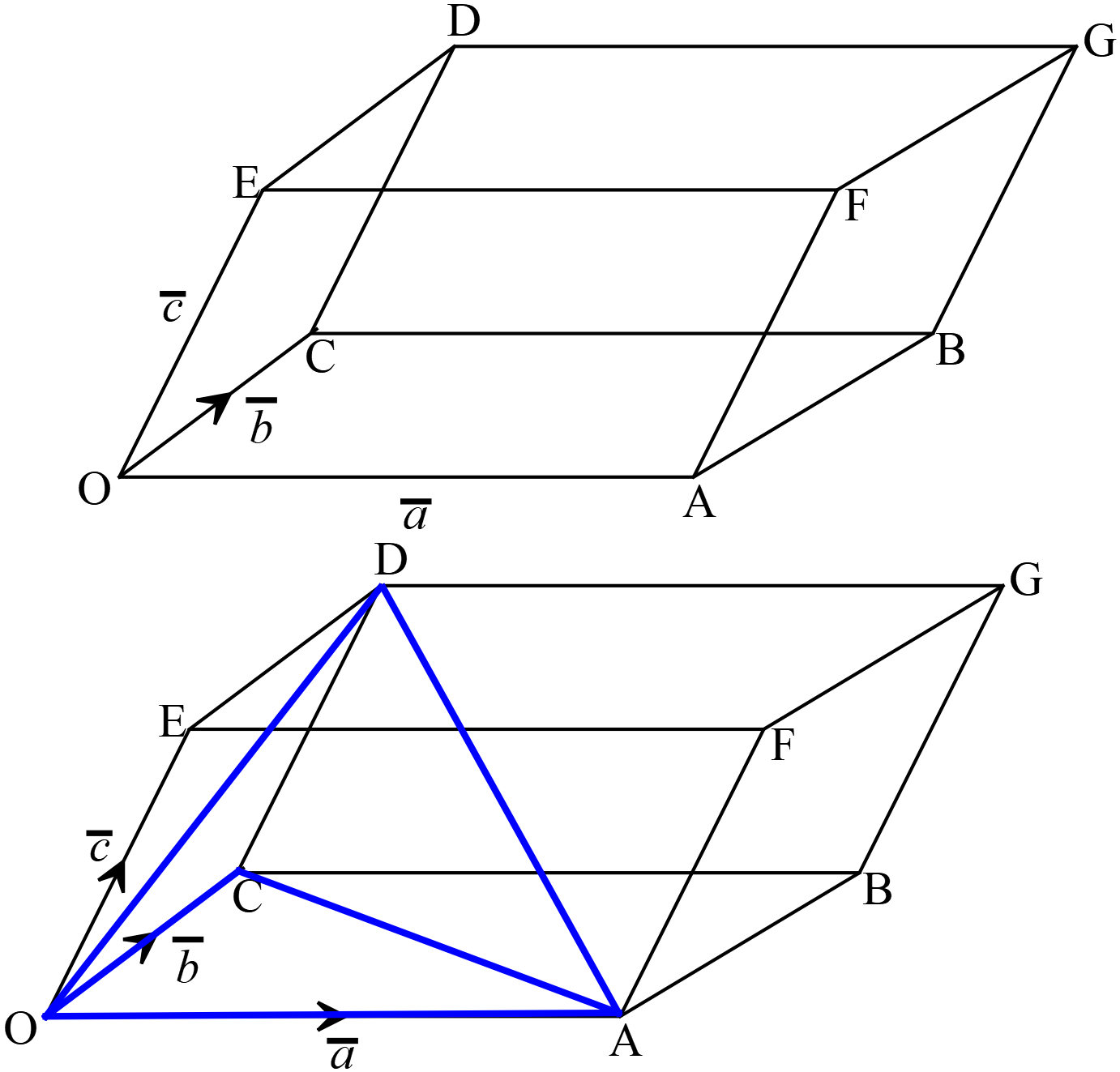যদি, \(OABCDEFG\) সামান্তরিক আকারের ঘন বস্তুর \(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{OC}=\overline{b}\) এবং \(\overrightarrow{OE}=\overline{c}\) হয় তবে, \(OABCDEFG\) সামান্তরিক আকারের ঘন বস্তুর আয়তন
\(=OABC\) ভূমির ক্ষেত্রফল \(\times\) উচ্চতা \(=[\overline{a} \ \overline{b} \ \overline{c}]\)
এখানে, \(OACD\) চতুস্তলকের আয়তন
\(=\frac{1}{3}OAC\) ভূমির ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{3}\times\frac{1}{2}OABC\) এর ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{6}OABC\) এর ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}]\)
অর্থাৎ কোনো চতুস্তলকের সমবিন্দু ধারসমূহ \(\overline{a},\) \(\overline{b}\) ও \(\overline{c}\) ভেক্টর দ্বারা সূচিত হলে ঐ চতুস্তলকটির আয়তন \(=\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}]\)
( প্রমাণিত )
কোনো সামান্তরিক আকারের ঘনবস্তুর সমবিন্দু ধারসমূহ \(\overline{a}, \ \overline{b}\) এবং \(\overline{c}\) দ্বারা সূচিত হলে \([\overline{a} \ \overline{b} \ \overline{c}]\) দ্বারা ঐ সামান্তরিক আকারের ঘনবস্তুর আয়তন নির্দেশিত হয়।
যদি, \(OABCDEFG\) সামান্তরিক আকারের ঘন বস্তুর \(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{OC}=\overline{b}\) এবং \(\overrightarrow{OE}=\overline{c}\) হয় তবে, \(OABCDEFG\) সামান্তরিক আকারের ঘন বস্তুর আয়তন\(=OABC\) ভূমির ক্ষেত্রফল \(\times\) উচ্চতা \(=[\overline{a} \ \overline{b} \ \overline{c}]\)
এখানে, \(OACD\) চতুস্তলকের আয়তন
\(=\frac{1}{3}OAC\) ভূমির ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{3}\times\frac{1}{2}OABC\) এর ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{6}OABC\) এর ক্ষেত্রফল \(\times\) উচ্চতা
\(=\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}]\)
অর্থাৎ কোনো চতুস্তলকের সমবিন্দু ধারসমূহ \(\overline{a},\) \(\overline{b}\) ও \(\overline{c}\) ভেক্টর দ্বারা সূচিত হলে ঐ চতুস্তলকটির আয়তন \(=\frac{1}{6}[\overline{a} \ \overline{b} \ \overline{c}]\)
( প্রমাণিত )
কোনো চতুস্তলকের চারটি শীর্ষবিন্দুর অবস্থান ভেক্টর \(\overline{a},\) \(\overline{b},\) \(\overline{c},\) \(\overline{d}\) হলে ঐ চতুস্তলকটির আয়তন,
\(\frac{1}{6}\{[\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}]\}.\)
প্রমাণঃ
\(\frac{1}{6}\{[\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}]\}.\)
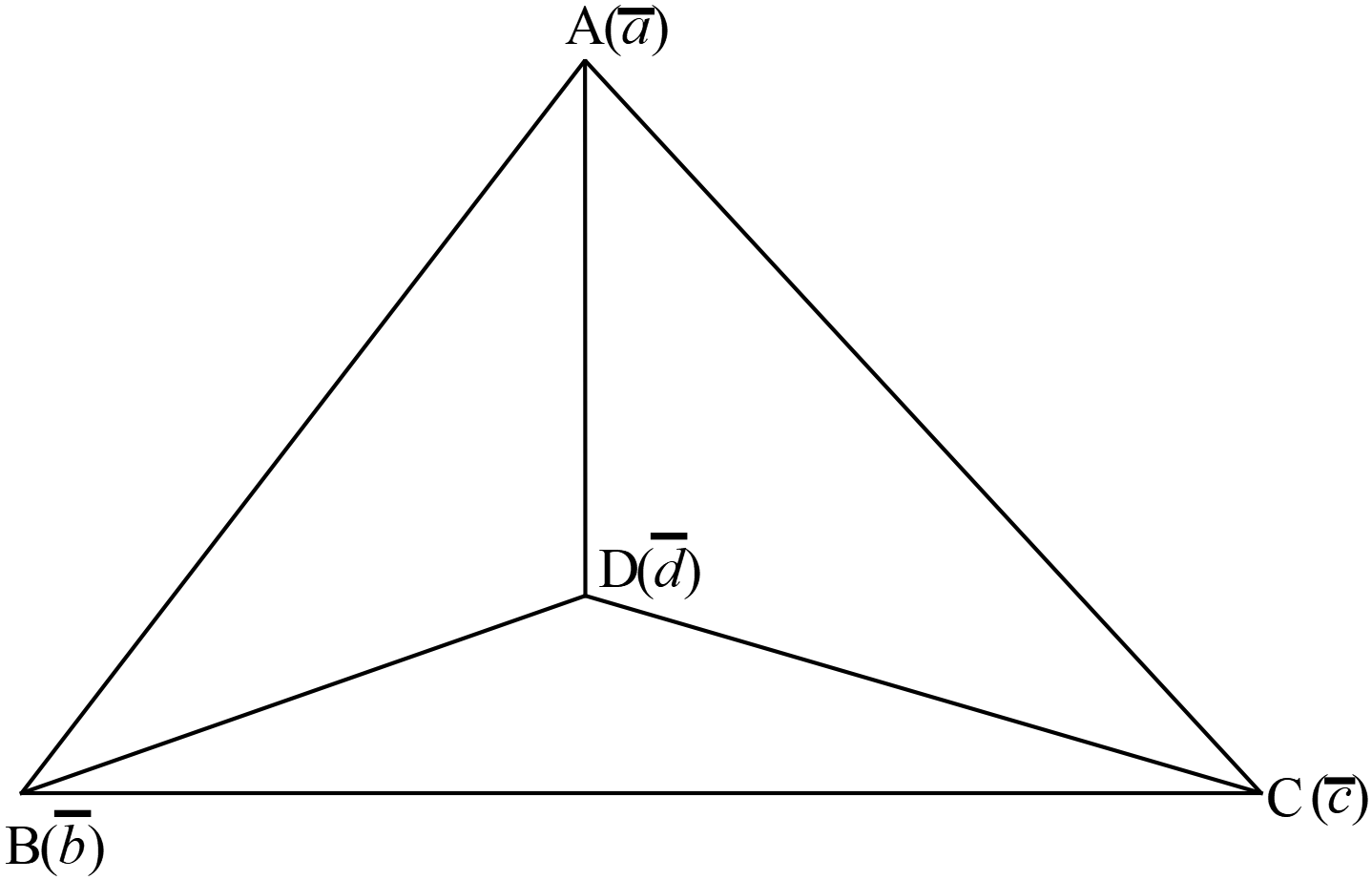ধরি, \(ABCD\) চতুস্তলকের \(A, \ B, \ C, \ D\) শীর্ষবিন্দু সমূহের অবস্থান ভেক্টর যথাক্রমে \(\overline{a}, \ \overline{b}, \ \overline{c}, \ \overline{d}\)
তাহলে, \(\overrightarrow{AD}=\overline{d}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
অনুরূপভাবে, \(\overrightarrow{BD}=\overline{d}-\overline{b}\)
\(\overrightarrow{CD}=\overline{d}-\overline{c}\)
এখন, \(ABCD\) চতুস্তলকের আয়তন
\(=\frac{1}{6}[\overrightarrow{AD} \ \overrightarrow{BD} \ \overrightarrow{CD}]\)
\(=\frac{1}{6}[\overline{d}-\overline{a} \ \overline{d}-\overline{b} \ \overline{d}-\overline{c}]\) ➜ \(\because \overrightarrow{AD}=\overline{d}-\overline{a}\)
\(\overrightarrow{BD}=\overline{d}-\overline{b}\)
এবং \(\overrightarrow{CD}=\overline{d}-\overline{c}\)
\(=\frac{1}{6}[(\overline{d}-\overline{a}). \{(\overline{d}-\overline{b})\times(\overline{d}-\overline{c})\}]\) ➜ \(\because [\overline{p} \ \overline{q} \ \overline{r}]=\overline{p}.\overline{q}\times\overline{r}\)
\(=\frac{1}{6}[(\overline{d}-\overline{a}). \{\overline{d}\times(\overline{d}-\overline{c})-\overline{b}\times(\overline{d}-\overline{c})\}]\)
\(=\frac{1}{6}[(\overline{d}-\overline{a}). \{\overline{d}\times\overline{d}-\overline{d}\times\overline{c}-\overline{b}\times\overline{d}+\overline{b}\times\overline{c}\}]\)
\(=\frac{1}{6}[(\overline{d}-\overline{a}). \{0+\overline{c}\times\overline{d}-\overline{b}\times\overline{d}+\overline{b}\times\overline{c}\}]\) ➜ \(\because \overline{d}\times\overline{d}=0\)
এবং \(\overline{d}\times\overline{c}=-\overline{c}\times\overline{d}\)
\(=\frac{1}{6}[\overline{d}.(\overline{c}\times\overline{d})-\overline{d}.(\overline{b}\times\overline{d})+\overline{d}.(\overline{b}\times\overline{c})-\overline{a}.(\overline{c}\times\overline{d})+\overline{a}.(\overline{b}\times\overline{d})-\overline{a}.(\overline{b}\times\overline{c})]\)
\(=\frac{1}{6}\{0-0+[\overline{d} \ \overline{b} \ \overline{c}]-[\overline{a} \ \overline{c} \ \overline{d}]+[\overline{a} \ \overline{b} \ \overline{d}]-[\overline{a} \ \overline{b} \ \overline{c}]\}\) ➜ \(\because \overline{d}.(\overline{c}\times\overline{d})=0\)
\(\overline{d}.(\overline{b}\times\overline{d})=0\)
\(\overline{d}.(\overline{b}\times\overline{c})=[\overline{d} \ \overline{b} \ \overline{c}]\)
\(\overline{a}.(\overline{c}\times\overline{d})=[\overline{a} \ \overline{c} \ \overline{d}]\)
\(\overline{a}.(\overline{b}\times\overline{d})=[\overline{a} \ \overline{b} \ \overline{d}]\)
এবং \(\overline{a}.(\overline{b}\times\overline{c})=[\overline{a} \ \overline{b} \ \overline{c}]\)
\(=\frac{1}{6}\{[\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}]\}\) ➜ \(\because [\overline{d} \ \overline{b} \ \overline{c}]=[\overline{b} \ \overline{c} \ \overline{d}]\)
\([\overline{a} \ \overline{c} \ \overline{d}]=[\overline{c} \ \overline{d} \ \overline{a}]\)
এবং \([\overline{a} \ \overline{b} \ \overline{d}]=[\overline{d} \ \overline{a} \ \overline{b}]\)
\(=\frac{1}{6}([\overline{b} \ \overline{c} \ \overline{d}]-[\overline{c} \ \overline{d} \ \overline{a}]+[\overline{d} \ \overline{a} \ \overline{b}]-[\overline{a} \ \overline{b} \ \overline{c}])\)
ইহাই নির্ণেয় চতুস্তলকের আয়তন
( প্রমাণিত )
যদি, \(ABC\) ত্রিভুজের \(A , \ B, \ C\) শীর্ষবিন্দু সমূহের অবস্থান ভেক্টর \(\overline{a},\) \(\overline{b},\) \(\overline{c}\) হয় তবে ত্রিভুজটির ক্ষেত্রফল,
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}+\overline{b}\times\overline{c}+\overline{c}\times\overline{a}|\)
প্রমাণঃ
\(\triangle=\frac{1}{2}|\overline{a}\times\overline{b}+\overline{b}\times\overline{c}+\overline{c}\times\overline{a}|\)
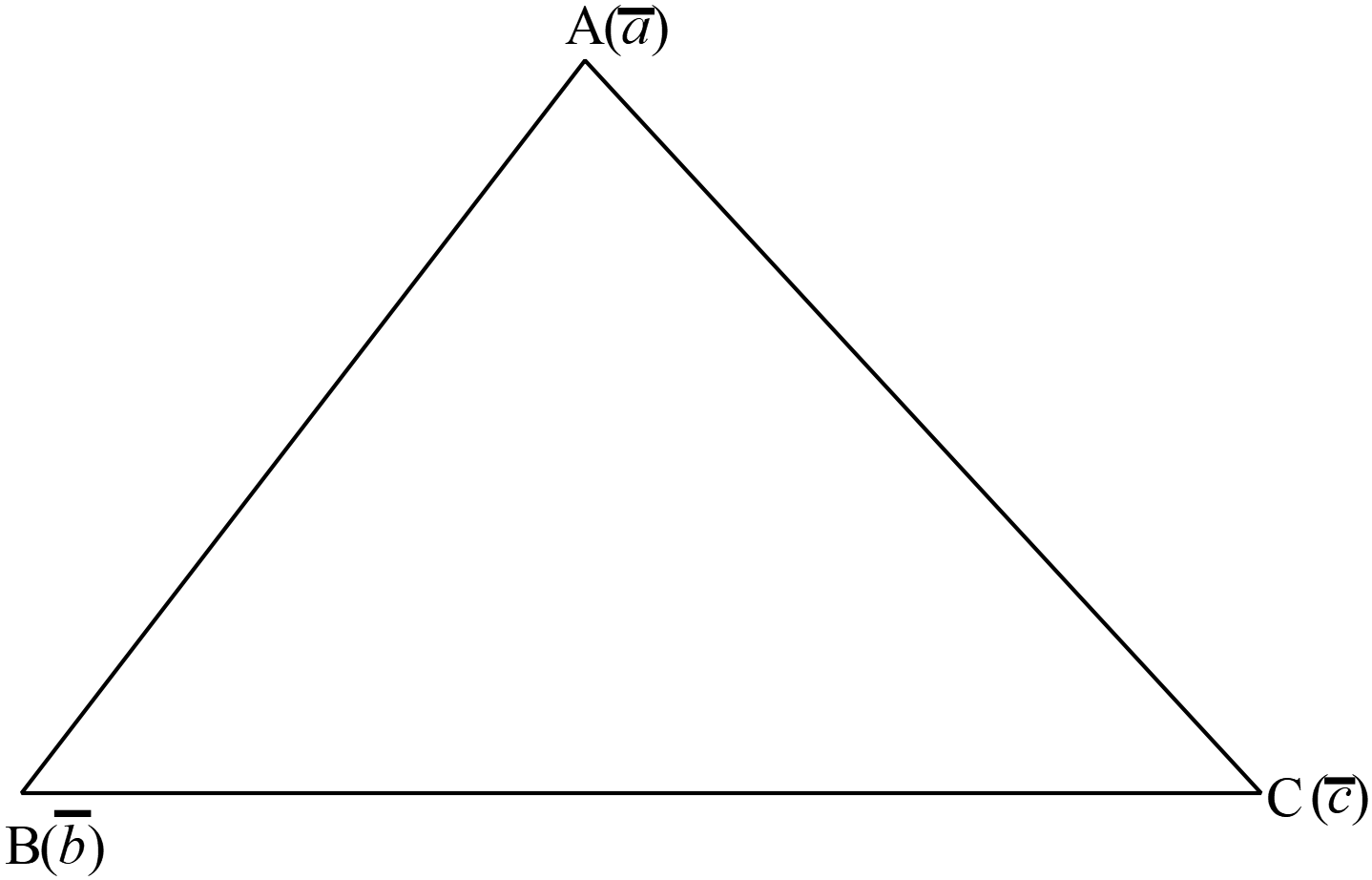দেওয়া আছে, \(ABC\) ত্রিভুজের \(A , \ B, \ C\) শীর্ষবিন্দু সমূহের অবস্থান ভেক্টর \(\overline{a},\) \(\overline{b},\) \(\overline{c}\)
তাহলে, \(\overrightarrow{AB}=\overline{b}-\overline{a}\) ➜ \(\because M(\overline{m}), \ N(\overline{n})\) হলে,
\(\overrightarrow{MN}=\overline{n}-\overline{m}\)
অনুরূপভাবে, \(\overrightarrow{AC}=\overline{c}-\overline{a}\)
এখন, \(ABC\) ত্রিভুজের ক্ষেত্রফল
\(=\frac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|\) ➜ \(\overrightarrow{PQ}, \ \overrightarrow{QR}\) কোনো ত্রিভুজের দুইটি বাহু নির্দেশ করলে,
ত্রিভুজের ক্ষেত্রফল \(=\frac{1}{2}|\overrightarrow{PQ}\times\overrightarrow{QR}|\)
\(=\frac{1}{2}|(\overline{b}-\overline{a})\times(\overline{c}-\overline{a})|\) ➜ \(\because \overrightarrow{AB}=\overline{b}-\overline{a}\)
এবং \(\overrightarrow{AC}=\overline{c}-\overline{a}\)
\(=\frac{1}{2}|\overline{b}\times(\overline{c}-\overline{a})-\overline{a}\times(\overline{c}-\overline{a})|\)
\(=\frac{1}{2}|\overline{b}\times\overline{c}-\overline{b}\times\overline{a}-\overline{a}\times\overline{c}+\overline{a}\times\overline{a}|\)
\(=\frac{1}{2}|\overline{b}\times\overline{c}+\overline{a}\times\overline{b}+\overline{c}\times\overline{a}+0|\) ➜ \(\because \overline{b}\times\overline{a}=-\overline{a}\times\overline{b}\)
\(\overline{a}\times\overline{c}=-\overline{c}\times\overline{a}\)
এবং \(\overline{a}\times\overline{a}=0\)
\(=\frac{1}{2}|\overline{a}\times\overline{b}+\overline{b}\times\overline{c}+\overline{c}\times\overline{a}|\)
ইহাই নির্ণেয় ত্রিভুজের ক্ষেত্রফল
( প্রমাণিত )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000002