এ অধ্যায়ে আমরা যে বিষয় গুলি আলোচনা করব।
- ঐতিহাসিক পটভূমি
- বলবিদ্যার প্রাথমিক ধারণা (Elementary Ideas of Mechanics)
- বস্তুর স্থিতি ও গতি (Rest and motion of objects)
- বল (Force)
- বলবিদ্যা (Mechanics)
- স্থিতিবিদ্যা (Statics)
- গতিবিদ্যা (Dynamics)
- বলের ক্রিয়াবিন্দুর স্থানান্তর বিধি (Transmissibility of point of application of force)
- বলের ক্রিয়া ও প্রতিক্রিয়া (Action and reaction of forces)
- বিভিন্ন প্রকারের বল (Different kinds of forces)
- টান ও উর্ধ্বচাপ (Tension and Overpressure)
- চাপ (Pressure)
- ঠেলা (Push)
- ঘর্ষণ (Friction)
- আকর্ষণ (Attraction)
- বিকর্ষণ (Repulsion)
- ওজন (Weight)
- অন্তকেন্দ্র (Inner centre)
- পরিকেন্দ্র (Circumcentre)
- ভরকেন্দ্র (Centroid)
- লম্বকেন্দ্র (Orthocentre)
- দুইটি বলের লব্ধি (Resultant of two forces)
- দুইটি বলের লব্ধির মাণ ও দিক (Magnitude and direction Of resultant of two forcess)
- বলের সামান্তরিক সূত্র (Parallelogram law of forces)
- বলবিদ্যায় ব্যবহৃত কয়েকটি প্রয়োজনীয় উপপাদ্য ও তার প্রমাণ (Some essential theorems used in mechanics and their proofs)
- বলের অংশক বা উপাংশ (Component of Forces)
- কোন নির্দিষ্ট দিকে একটি বলের অংশক বা উপাংশ নির্ণয়-বলের সাইন সূত্র (Determine the component or fraction of a force in a given direction)
- বলের লম্বাংশ (Resolved parts of forces)
- লম্বাংশের উপপাদ্য (Prolongation Theorem)
- লম্বাংশের সাহায্যে দুইটি বলের লব্ধির মাণ ও দিক নির্ণয় (Determine the magnitude and direction of acceleration of two Forces with the help of Prolongation Theorem)
- সমবিন্দুগামী যে কোন সংখ্যক একতলীয় বলের লব্ধি নির্ণয় (Determine the Resultant of any number of concentric Forces)
- প্রয়োজনীয় সূত্রাবলী (Required formulas)
- অধ্যায় \(8A\)-এর উদাহরণসমুহ
- অধ্যায় \(8A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(8A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(8A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(8A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
স্থিতিবিদ্যা
Statics

স্যার আইজ্যাক নিউটন
( ১৬৪২-১৭২৭ )
স্যার আইজ্যাক নিউটন বলের মৌলিক ধর্মাবলি ও সামান্তরিক সূত্র আবিষ্কার করেন। এজন্য নিউটনকে স্থিতিবিদ্যার জনক বলা হয়।
পদার্থ বিজ্ঞানের (Physical science) একটি শাখা হিসাবে বলবিদ্যাকে সংজ্ঞায়িত করা হয় যা বস্তুর স্থিতি বা গতির ধর্ম নিয়ে আলোচনা করে। যে কোনো পেশাগত ও কারিগরি সমস্যা সমাধানের ক্ষেত্রে বিজ্ঞানের এ শাখার জুড়ি মেলা ভার। বলবিদ্যার শাখা হিসাবে স্থিতিবিদ্যাও এর ব্যতিক্রম নয়। স্থিতিবিদ্যা হচ্ছে Rigid body mechanics এর অংশ যা বস্তুর ভারসাম্য, সাম্যাবস্থা ও বস্তুর অবস্থানের প্রকৃতি ব্যাখ্যা করে। জ্যামিতির প্রায়োগিক জ্ঞান বলের মূলনীতির উপর ভিত্তি করে স্থিতিবিদ্যার মূলনীতি প্রণিত হয়। প্রাচীনকাল হতেই স্থিতিবিদ্যার ব্যবহার চলে আসছে। পারিপার্শিক বস্তুর সাপেক্ষে কোনো বস্তুর অবস্থানের পরিবর্তন না হলে তাকে স্থিতিশীল বলা হয়।
স্থিতিবিদ্যায় বলের ক্রিয়াবিদ্যা, ক্রিয়ারেখা, ক্রিয়ার মাণ ও দিক সম্পর্কে সুস্পষ্ট ধারণার প্রয়োজন। এছাড়া টান, আকর্ষণ, বিকর্ষণ, প্রতিক্রিয়া, ঘর্ষণ, ওজন, লব্ধিবল ইত্যাদি সম্পর্কে জ্ঞান থাকা আবশ্যক। সমস্ত স্থিতিবিদ্যার চারটি ভিত্তি হলো বলসমূহের নিরোপেক্ষতার সূত্র, বল স্থানান্তরিত-করণের সূত্র, ক্রিয়া ও প্রতিক্রিয়ার সূত্র এবং বলের সামান্তরিক সূত্র।
প্রাচীন গ্রিসে দুইটি ভিন্ন বিষয়বস্তু উদ্ঘাটনের ক্ষেত্রে স্থিতিবিদ্যার অবতারণা হয়। প্রথমটি হচ্ছে লিভার, হেলানো তল ও এর ভারসাম্য এবং অপরটি হচ্ছে পরিবেশে বিদ্যমান বস্তুর স্থির ধর্মের ব্যখ্যা। প্রাচীনকালেই মানুষ পাথর ছোঁড়া, তীর নিক্ষেপ ও লিভারের ব্যবহারে স্থিতিবিদ্যার মূলনীতি ব্যবহার করে। প্রাচীন বিজ্ঞানী হিপোক্রেটাস  হিপোক্রেটাস (৪৬০ খ্রিস্টপূর্বাব্দ - ৩৬০ খ্রিস্টপূর্বাব্দ), যিনি দ্বিতীয় হিপোক্রেটিস নামেও পরিচিত, পেরিক্লেসের যুগের একজন প্রাচীন গ্রিক চিকিৎসক ছিলেন, যাঁকে চিকিৎসাশাস্ত্রের ইতিহাসে সর্বাধিক উল্লেখযোগ্য ব্যক্তিদের মধ্যে একজন বলে গণ্য করা হয়। হিপোক্রেটীয় চিকিৎসাশৈলীর উদ্ভাবনের স্বীকৃতিতে তাঁকে পশ্চিমা চিকিৎসাশাস্ত্রের পিতা বলে অভিহিত করা হয়ে থাকে। তাঁর শৈলী দর্শন ও ধর্মীয় রীতিনীতি থেকে পৃথক করে চিকিৎসাশাস্ত্রকে একটি পেশা হিসেবে প্রতিষ্ঠিত করে প্রাচীন গ্রিক চিকিৎসাশাস্ত্রে বৈপ্লবিক পরিবর্তন আনে। হিপোক্রেটাস বলেছিলেন, হাঁটাহাঁটি হল সবচেয়ে সেরা ওষুধ। গ্রিসের এই বিখ্যাত ফিজিশিয়ানকে বলা হয় মেডিসিনের জনক। হিপোক্রেটাস নিঃসন্দেহে একজন স্মার্ট লোক ছিলেন। আজকাল অনেক দামী গবেষণায় প্রমাণিত যে হাঁটাহাঁটি করা আমাদের দেহের জন্য কতবেশি জরুরি। গবেষণাগুলোর ফলাফল সত্যিই প্রভাবিত করার মতো। হাঁটায় ডায়বেটিস ও হৃদরোগ দুটিই কমে। সেইসঙ্গে কমে ব্লাড প্রেশার, বাড়ে হাড়ের ঘনত্ব, ওজন তো কমেই আরও অনেক উপকার হয় নিয়মিত হাঁটাহাঁটি করলে।, টলেমি
হিপোক্রেটাস (৪৬০ খ্রিস্টপূর্বাব্দ - ৩৬০ খ্রিস্টপূর্বাব্দ), যিনি দ্বিতীয় হিপোক্রেটিস নামেও পরিচিত, পেরিক্লেসের যুগের একজন প্রাচীন গ্রিক চিকিৎসক ছিলেন, যাঁকে চিকিৎসাশাস্ত্রের ইতিহাসে সর্বাধিক উল্লেখযোগ্য ব্যক্তিদের মধ্যে একজন বলে গণ্য করা হয়। হিপোক্রেটীয় চিকিৎসাশৈলীর উদ্ভাবনের স্বীকৃতিতে তাঁকে পশ্চিমা চিকিৎসাশাস্ত্রের পিতা বলে অভিহিত করা হয়ে থাকে। তাঁর শৈলী দর্শন ও ধর্মীয় রীতিনীতি থেকে পৃথক করে চিকিৎসাশাস্ত্রকে একটি পেশা হিসেবে প্রতিষ্ঠিত করে প্রাচীন গ্রিক চিকিৎসাশাস্ত্রে বৈপ্লবিক পরিবর্তন আনে। হিপোক্রেটাস বলেছিলেন, হাঁটাহাঁটি হল সবচেয়ে সেরা ওষুধ। গ্রিসের এই বিখ্যাত ফিজিশিয়ানকে বলা হয় মেডিসিনের জনক। হিপোক্রেটাস নিঃসন্দেহে একজন স্মার্ট লোক ছিলেন। আজকাল অনেক দামী গবেষণায় প্রমাণিত যে হাঁটাহাঁটি করা আমাদের দেহের জন্য কতবেশি জরুরি। গবেষণাগুলোর ফলাফল সত্যিই প্রভাবিত করার মতো। হাঁটায় ডায়বেটিস ও হৃদরোগ দুটিই কমে। সেইসঙ্গে কমে ব্লাড প্রেশার, বাড়ে হাড়ের ঘনত্ব, ওজন তো কমেই আরও অনেক উপকার হয় নিয়মিত হাঁটাহাঁটি করলে।, টলেমি  ক্লডিয়াস টলেমিয়াস (Claudius Ptolemy) (খৃষ্টপূর্ব ৯০ – খৃষ্টপূর্ব ১৬৮), যিনি টলেমি নামে সমাধিক পরিচিত, একজন গ্রিক গণিতবিদ, ভূগোলবিদ, জ্যোতির্বিদ, ও জ্যোতিষ। তিনি রোম-শাসিত মিশরের ইজিপ্টাস নামক প্রদেশের অধিবাসী ছিলেন। ধারণা করা হয় যা, তাঁর জন্ম মিশরেই। , আর্কিমিডিস
ক্লডিয়াস টলেমিয়াস (Claudius Ptolemy) (খৃষ্টপূর্ব ৯০ – খৃষ্টপূর্ব ১৬৮), যিনি টলেমি নামে সমাধিক পরিচিত, একজন গ্রিক গণিতবিদ, ভূগোলবিদ, জ্যোতির্বিদ, ও জ্যোতিষ। তিনি রোম-শাসিত মিশরের ইজিপ্টাস নামক প্রদেশের অধিবাসী ছিলেন। ধারণা করা হয় যা, তাঁর জন্ম মিশরেই। , আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। , ও এরিস্টটলের
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। , ও এরিস্টটলের  এরিস্টটল (খ্রিষ্টপূর্ব ৩৮৪ – ৭ই মার্চ, খ্রিষ্টপূর্ব ৩২২) বিশ্ববিখ্যাত গ্রিক বিজ্ঞানী ও দার্শনিক। তাঁকে প্রাণীবিজ্ঞানের জনক বলা হয়। এছাড়া প্লেটোর সাথে যৌথভাবে তাকে "পশ্চিমা দর্শনের জনক" বলে অভিহিত করা হয়। হাত ধরেই স্থিতিবিদ্যার প্রায়োগিক শাখার উৎপত্তি। আধুনিক বিজ্ঞানীদের মধ্যে ষষ্ঠদশ শতাব্দীতে ডাচ গণিতবিদ সাইমন স্টোভন
এরিস্টটল (খ্রিষ্টপূর্ব ৩৮৪ – ৭ই মার্চ, খ্রিষ্টপূর্ব ৩২২) বিশ্ববিখ্যাত গ্রিক বিজ্ঞানী ও দার্শনিক। তাঁকে প্রাণীবিজ্ঞানের জনক বলা হয়। এছাড়া প্লেটোর সাথে যৌথভাবে তাকে "পশ্চিমা দর্শনের জনক" বলে অভিহিত করা হয়। হাত ধরেই স্থিতিবিদ্যার প্রায়োগিক শাখার উৎপত্তি। আধুনিক বিজ্ঞানীদের মধ্যে ষষ্ঠদশ শতাব্দীতে ডাচ গণিতবিদ সাইমন স্টোভন  সাইমন স্টিভিন (ডাচ: [simɔn steːvɪn]; 1548-1620), কখনও কখনও স্টিভিনাস নামে পরিচিত, ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিজ্ঞানী এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং বাস্তব উভয়, বিজ্ঞান ও প্রকৌশল অনেক ক্ষেত্রে বিভিন্ন অবদান। ( 1548-1620) বলের ত্রিভুজ সূত্র প্রকাশ করে এর সাথে সামান্তরিক সূত্রের সম্পর্ক প্রতিষ্ঠা করেন। পরবর্তিতে ফরাসি গণিতবিদ ও ধর্মতত্ত্ববিদ বার্নাড লামি
সাইমন স্টিভিন (ডাচ: [simɔn steːvɪn]; 1548-1620), কখনও কখনও স্টিভিনাস নামে পরিচিত, ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিজ্ঞানী এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং বাস্তব উভয়, বিজ্ঞান ও প্রকৌশল অনেক ক্ষেত্রে বিভিন্ন অবদান। ( 1548-1620) বলের ত্রিভুজ সূত্র প্রকাশ করে এর সাথে সামান্তরিক সূত্রের সম্পর্ক প্রতিষ্ঠা করেন। পরবর্তিতে ফরাসি গণিতবিদ ও ধর্মতত্ত্ববিদ বার্নাড লামি  বার্নার্ড ল্যামি (1640 - 1715) একজন ফ্রেঞ্চ গণিতবিদ যিনি জ্যামিতি এবং যান্ত্রিক বিষয়ে লিখেছিলেন। (1640-1715) সামান্তরিক সূত্রের ওপর কাজ করে স্থিতিবিদ্যাকে আধুনিক শাখা হিসেবে প্রতিষ্ঠা করেন। বর্তমানে বড় বড় দালান, সেতু, অত্যাধুনিক শক্তিশালী বোমা ও মেশিনারী যন্ত্রপাতি তৈরিতে স্থিতিবিদ্যার মূলনীতির অবদান অনস্বীকার্য।
বার্নার্ড ল্যামি (1640 - 1715) একজন ফ্রেঞ্চ গণিতবিদ যিনি জ্যামিতি এবং যান্ত্রিক বিষয়ে লিখেছিলেন। (1640-1715) সামান্তরিক সূত্রের ওপর কাজ করে স্থিতিবিদ্যাকে আধুনিক শাখা হিসেবে প্রতিষ্ঠা করেন। বর্তমানে বড় বড় দালান, সেতু, অত্যাধুনিক শক্তিশালী বোমা ও মেশিনারী যন্ত্রপাতি তৈরিতে স্থিতিবিদ্যার মূলনীতির অবদান অনস্বীকার্য।
 হিপোক্রেটাস (৪৬০ খ্রিস্টপূর্বাব্দ - ৩৬০ খ্রিস্টপূর্বাব্দ), যিনি দ্বিতীয় হিপোক্রেটিস নামেও পরিচিত, পেরিক্লেসের যুগের একজন প্রাচীন গ্রিক চিকিৎসক ছিলেন, যাঁকে চিকিৎসাশাস্ত্রের ইতিহাসে সর্বাধিক উল্লেখযোগ্য ব্যক্তিদের মধ্যে একজন বলে গণ্য করা হয়। হিপোক্রেটীয় চিকিৎসাশৈলীর উদ্ভাবনের স্বীকৃতিতে তাঁকে পশ্চিমা চিকিৎসাশাস্ত্রের পিতা বলে অভিহিত করা হয়ে থাকে। তাঁর শৈলী দর্শন ও ধর্মীয় রীতিনীতি থেকে পৃথক করে চিকিৎসাশাস্ত্রকে একটি পেশা হিসেবে প্রতিষ্ঠিত করে প্রাচীন গ্রিক চিকিৎসাশাস্ত্রে বৈপ্লবিক পরিবর্তন আনে। হিপোক্রেটাস বলেছিলেন, হাঁটাহাঁটি হল সবচেয়ে সেরা ওষুধ। গ্রিসের এই বিখ্যাত ফিজিশিয়ানকে বলা হয় মেডিসিনের জনক। হিপোক্রেটাস নিঃসন্দেহে একজন স্মার্ট লোক ছিলেন। আজকাল অনেক দামী গবেষণায় প্রমাণিত যে হাঁটাহাঁটি করা আমাদের দেহের জন্য কতবেশি জরুরি। গবেষণাগুলোর ফলাফল সত্যিই প্রভাবিত করার মতো। হাঁটায় ডায়বেটিস ও হৃদরোগ দুটিই কমে। সেইসঙ্গে কমে ব্লাড প্রেশার, বাড়ে হাড়ের ঘনত্ব, ওজন তো কমেই আরও অনেক উপকার হয় নিয়মিত হাঁটাহাঁটি করলে।, টলেমি
হিপোক্রেটাস (৪৬০ খ্রিস্টপূর্বাব্দ - ৩৬০ খ্রিস্টপূর্বাব্দ), যিনি দ্বিতীয় হিপোক্রেটিস নামেও পরিচিত, পেরিক্লেসের যুগের একজন প্রাচীন গ্রিক চিকিৎসক ছিলেন, যাঁকে চিকিৎসাশাস্ত্রের ইতিহাসে সর্বাধিক উল্লেখযোগ্য ব্যক্তিদের মধ্যে একজন বলে গণ্য করা হয়। হিপোক্রেটীয় চিকিৎসাশৈলীর উদ্ভাবনের স্বীকৃতিতে তাঁকে পশ্চিমা চিকিৎসাশাস্ত্রের পিতা বলে অভিহিত করা হয়ে থাকে। তাঁর শৈলী দর্শন ও ধর্মীয় রীতিনীতি থেকে পৃথক করে চিকিৎসাশাস্ত্রকে একটি পেশা হিসেবে প্রতিষ্ঠিত করে প্রাচীন গ্রিক চিকিৎসাশাস্ত্রে বৈপ্লবিক পরিবর্তন আনে। হিপোক্রেটাস বলেছিলেন, হাঁটাহাঁটি হল সবচেয়ে সেরা ওষুধ। গ্রিসের এই বিখ্যাত ফিজিশিয়ানকে বলা হয় মেডিসিনের জনক। হিপোক্রেটাস নিঃসন্দেহে একজন স্মার্ট লোক ছিলেন। আজকাল অনেক দামী গবেষণায় প্রমাণিত যে হাঁটাহাঁটি করা আমাদের দেহের জন্য কতবেশি জরুরি। গবেষণাগুলোর ফলাফল সত্যিই প্রভাবিত করার মতো। হাঁটায় ডায়বেটিস ও হৃদরোগ দুটিই কমে। সেইসঙ্গে কমে ব্লাড প্রেশার, বাড়ে হাড়ের ঘনত্ব, ওজন তো কমেই আরও অনেক উপকার হয় নিয়মিত হাঁটাহাঁটি করলে।, টলেমি  ক্লডিয়াস টলেমিয়াস (Claudius Ptolemy) (খৃষ্টপূর্ব ৯০ – খৃষ্টপূর্ব ১৬৮), যিনি টলেমি নামে সমাধিক পরিচিত, একজন গ্রিক গণিতবিদ, ভূগোলবিদ, জ্যোতির্বিদ, ও জ্যোতিষ। তিনি রোম-শাসিত মিশরের ইজিপ্টাস নামক প্রদেশের অধিবাসী ছিলেন। ধারণা করা হয় যা, তাঁর জন্ম মিশরেই। , আর্কিমিডিস
ক্লডিয়াস টলেমিয়াস (Claudius Ptolemy) (খৃষ্টপূর্ব ৯০ – খৃষ্টপূর্ব ১৬৮), যিনি টলেমি নামে সমাধিক পরিচিত, একজন গ্রিক গণিতবিদ, ভূগোলবিদ, জ্যোতির্বিদ, ও জ্যোতিষ। তিনি রোম-শাসিত মিশরের ইজিপ্টাস নামক প্রদেশের অধিবাসী ছিলেন। ধারণা করা হয় যা, তাঁর জন্ম মিশরেই। , আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। , ও এরিস্টটলের
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। , ও এরিস্টটলের  এরিস্টটল (খ্রিষ্টপূর্ব ৩৮৪ – ৭ই মার্চ, খ্রিষ্টপূর্ব ৩২২) বিশ্ববিখ্যাত গ্রিক বিজ্ঞানী ও দার্শনিক। তাঁকে প্রাণীবিজ্ঞানের জনক বলা হয়। এছাড়া প্লেটোর সাথে যৌথভাবে তাকে "পশ্চিমা দর্শনের জনক" বলে অভিহিত করা হয়। হাত ধরেই স্থিতিবিদ্যার প্রায়োগিক শাখার উৎপত্তি। আধুনিক বিজ্ঞানীদের মধ্যে ষষ্ঠদশ শতাব্দীতে ডাচ গণিতবিদ সাইমন স্টোভন
এরিস্টটল (খ্রিষ্টপূর্ব ৩৮৪ – ৭ই মার্চ, খ্রিষ্টপূর্ব ৩২২) বিশ্ববিখ্যাত গ্রিক বিজ্ঞানী ও দার্শনিক। তাঁকে প্রাণীবিজ্ঞানের জনক বলা হয়। এছাড়া প্লেটোর সাথে যৌথভাবে তাকে "পশ্চিমা দর্শনের জনক" বলে অভিহিত করা হয়। হাত ধরেই স্থিতিবিদ্যার প্রায়োগিক শাখার উৎপত্তি। আধুনিক বিজ্ঞানীদের মধ্যে ষষ্ঠদশ শতাব্দীতে ডাচ গণিতবিদ সাইমন স্টোভন  সাইমন স্টিভিন (ডাচ: [simɔn steːvɪn]; 1548-1620), কখনও কখনও স্টিভিনাস নামে পরিচিত, ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিজ্ঞানী এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং বাস্তব উভয়, বিজ্ঞান ও প্রকৌশল অনেক ক্ষেত্রে বিভিন্ন অবদান। ( 1548-1620) বলের ত্রিভুজ সূত্র প্রকাশ করে এর সাথে সামান্তরিক সূত্রের সম্পর্ক প্রতিষ্ঠা করেন। পরবর্তিতে ফরাসি গণিতবিদ ও ধর্মতত্ত্ববিদ বার্নাড লামি
সাইমন স্টিভিন (ডাচ: [simɔn steːvɪn]; 1548-1620), কখনও কখনও স্টিভিনাস নামে পরিচিত, ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিজ্ঞানী এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং বাস্তব উভয়, বিজ্ঞান ও প্রকৌশল অনেক ক্ষেত্রে বিভিন্ন অবদান। ( 1548-1620) বলের ত্রিভুজ সূত্র প্রকাশ করে এর সাথে সামান্তরিক সূত্রের সম্পর্ক প্রতিষ্ঠা করেন। পরবর্তিতে ফরাসি গণিতবিদ ও ধর্মতত্ত্ববিদ বার্নাড লামি  বার্নার্ড ল্যামি (1640 - 1715) একজন ফ্রেঞ্চ গণিতবিদ যিনি জ্যামিতি এবং যান্ত্রিক বিষয়ে লিখেছিলেন। (1640-1715) সামান্তরিক সূত্রের ওপর কাজ করে স্থিতিবিদ্যাকে আধুনিক শাখা হিসেবে প্রতিষ্ঠা করেন। বর্তমানে বড় বড় দালান, সেতু, অত্যাধুনিক শক্তিশালী বোমা ও মেশিনারী যন্ত্রপাতি তৈরিতে স্থিতিবিদ্যার মূলনীতির অবদান অনস্বীকার্য।
বার্নার্ড ল্যামি (1640 - 1715) একজন ফ্রেঞ্চ গণিতবিদ যিনি জ্যামিতি এবং যান্ত্রিক বিষয়ে লিখেছিলেন। (1640-1715) সামান্তরিক সূত্রের ওপর কাজ করে স্থিতিবিদ্যাকে আধুনিক শাখা হিসেবে প্রতিষ্ঠা করেন। বর্তমানে বড় বড় দালান, সেতু, অত্যাধুনিক শক্তিশালী বোমা ও মেশিনারী যন্ত্রপাতি তৈরিতে স্থিতিবিদ্যার মূলনীতির অবদান অনস্বীকার্য।
বলবিদ্যার প্রাথমিক ধারণা
Elementary Ideas of Mechanics
'বলবিদ্যা' শব্দটির বিশ্লেষণ করলে এর অর্থ দাঁড়ায় বল সংশ্লিষ্ট জ্ঞান। সুতরাং বলবিদ্যা অধ্যয়ন করলে, বল কি, তার প্রকারভেদ এবং প্রয়োগ সম্বন্ধে সম্যক জ্ঞান অর্জন সম্ভব। আমরা জানি প্রয়োজন, উদ্দীপনা ও উৎসাহ এই তিনটি বিষয়ের কারণেই মানুষ নতুন নতুন আবিষ্কার করে চলেছে। বর্তমান এই আধুনিক বিশ্বের অতি সহজসাধ্য দুইটি শব্দ হচ্ছে বস্তুর স্থিতি ও গতি, এই শব্দগুলি সম্পর্কে গাণিতিক ধারণা পাওয়ার জন্য 'বল' সম্পর্কে জ্ঞান অর্জন অত্যাবশ্যক।
বস্তুর স্থিতি ও গতি
Rest and motion of objects
বস্তুর স্থিতি ও গতিঃ যদি সময়ের পরিবর্তনে কোনো বস্তু তার পারিপার্শিক বস্তুসমুহের সাপেক্ষে অবস্থান পরিবর্তন না করে তবে বস্তুটিকে স্থিতিশীল বা স্থির বস্তু এবং বস্তুর অবস্থানকে স্থিতি অবস্থা বলা হয়।
আর যদি পারিপার্শিক বস্তুসমুহের সাপেক্ষে অবস্থান পরিবর্তন করে তবে ঐ বস্তুটিকে গতিশীল বস্তু এবং তার অবস্থাকে গতিশীল অবস্থা বলা হয়।
দার্শনিক ও বিজ্ঞানীদের মতে, 'বিশ্বব্রহ্মান্ডে কোনো বস্তুই স্থির নয়'। কেননা সৌরজগতের প্রতিটি গ্রহ ও নক্ষত্রই গতিশীল। তাহলে স্থিতির প্রসঙ্গ কেন আসছে, এই বিষয়টি স্পষ্টভাবে বোঝানোর জন্য নিম্নে উদাহরণ দেওয়া হলঃ
ক্লাসে পাঠদানের সময় শিক্ষক চেয়ারে বসে শিক্ষার্থীদের জিজ্ঞেস করলেন, আমি স্থির না গতিশীল এর সঠিক উত্তর কী হবে? সঠিক উত্তর হল- 'গতিশীল'। কারণ,ইযে পৃথিবীতে দাঁড়িয়ে শিক্ষক পাঠদান করছেন সেই পৃথিবী প্রচন্ড বেগে সূর্যের চতুর্দিকে এবং নিজ অক্ষের চতুর্দিকে পরিভ্রমণ করছে। কিন্তু যদি প্রশ্নটি এমন হতো, 'আমি তোমাদের সাপেক্ষে স্থির না গতিশীল?' তাহলে সঠিক উত্তর হতো 'স্থির'। অর্থাৎ বস্তুর স্থিতি অবস্থা ও গিতিশীল অবস্থা একটি আপেক্ষিক বিষয় যা Thoeory of Relativity নামে পদার্থবিদ্যা ও ফলিত গণিতের উচ্চতর শ্রেণীতে পাঠ্য বিষয় হিসেবে অন্তর্ভুক্ত।
আমরা বস্তুটিকে স্থির বা গতিশীল বলার জন্য অবশ্যই পারিপার্শিক বা চতুর্দিকে অবস্থিত বস্তুর সাপেক্ষেই বিবেচনা করব। কারণ ব্যবহারিক জীবনে এটি আমাদের সর্বদা প্রয়োজন, অর্থাৎ এর গুরুত্ব অপরিসীম।
বল
Force
বলঃ যা কোনো স্থির বস্তুর উপর ক্রিয়া করে তাকে গতিশীল করে বা করতে চায় এবং কোনো গতিশীল বস্তুর উপর ক্রিয়া করে তার গতির পরিবর্তন করে বা করতে চায় তাকে বল বলে।
যেমনঃ একটি ফুটবল একজন খেলোয়াড় হতে অন্য খেলোয়াড়ের নিকট এমনিতেই যায় না। ফুটবলের উপর বল প্রয়োগের ফলেই সেটা ঘটে। আবার গোল করার লক্ষে ফুটবলটি ছুড়ে দিলে গোলকিপার তা ধরে ফেলে এ ক্ষেত্রেও তাকে বল প্রয়োগ করতে হয়েছে।
যেমনঃ একটি ফুটবল একজন খেলোয়াড় হতে অন্য খেলোয়াড়ের নিকট এমনিতেই যায় না। ফুটবলের উপর বল প্রয়োগের ফলেই সেটা ঘটে। আবার গোল করার লক্ষে ফুটবলটি ছুড়ে দিলে গোলকিপার তা ধরে ফেলে এ ক্ষেত্রেও তাকে বল প্রয়োগ করতে হয়েছে।
বলবিদ্যা
Mechanics
বলবিদ্যাঃ যে শাস্ত্রে কোনো বস্তুর স্থিতি বা গতিশীল অবস্থা সম্পর্কে আলোচনা করা হয় তাকে বলবিদ্যা বলা হয়। বলবিদ্যা দুইটি অংশে বিভক্ত।
যেমনঃ (i) স্থিতিবিদ্যা, (ii) গতিবিদ্যা।
যেমনঃ (i) স্থিতিবিদ্যা, (ii) গতিবিদ্যা।
স্থিতিবিদ্যা
Statics
স্থিতিবিদ্যাঃ বলবিদ্যার যে শাখায় স্থিতিশীল বস্তুর উপর কার্যরত বল সম্পর্কিত আলোচনা করা হয় তাকে স্থিতিবিদ্যা বলা হয়।
গতিবিদ্যা
Dynamics
গতিবিদ্যাঃ বলবিদ্যার যে শাখায় গতিশীল বস্তুর উপর কার্যরত বল সম্পর্কিত আলোচনা করা হয় তাকে গতিবিদ্যা বলা হয়।
বলের ক্রিয়াবিন্দুর স্থানান্তর বিধি
Transmissibility of point of application of force
একটি বল কোনো জড়বস্তুর কোনো বিন্দুতে ক্রিয়া করলে যে ফলাফল পাওয়া যায় বস্তুর উপর অবস্থিত ঐ বলের ক্রিয়া রেখার উপর যে কোনো বিন্দুতে বলটিকে প্রয়োগ করা হলেও একই ফলাফল পাওয়া যায়।
মনে করি,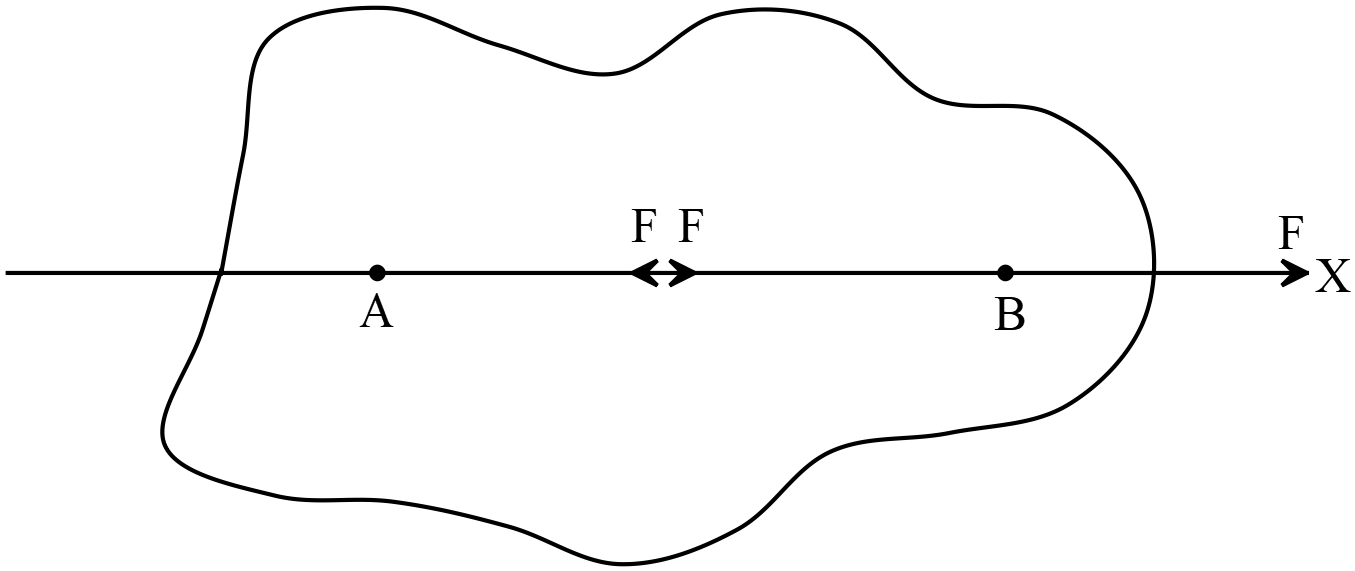 \(F\) বলটি কোনো জড়বস্তুর \(A\) বিন্দুতে \(AX\) রেখা বরাবর ক্রিয়া করে। \(AX\) রেখার উপর তথা জড়বস্তুর উপর একটি বিন্দু \(B\) নেই। এখন \(B\) তে \(BA\) এবং \(BX\) বরাবর দুইটি সমান বল \(F\) প্রয়োগ করি। সমান ও বিপরীতমুখী বল প্রয়োগের ফলে বস্তুটির অবস্থানের কোনো পরিবর্তন হবে না।
এখন \(A\) বিন্দুতে \(AB\) বরবর কার্যরত \(F\) বল এবং \(B\) বিন্দুতে \(BA\) বরাবর কার্যরত \(F\) বল পরস্পর সমান ও বিপরীতমুখী হওয়ায় তারা একে অপরকে নিষ্ক্রিয় করবে।
সুতরাং বস্তুটির উপর একমাত্র কার্যরত বল হলো \(B\) বিন্দুতে \(BX\) বরাবর ক্রিয়ারত \(F\) বল। এই বলটি \(A\) বিন্দুতে \(AX\) বরাবর ক্রিয়ারত \(F\) বলের সমান। অতএব বলের ক্রিয়াবিন্দু বলের কার্যরেখার যেকোনো বিন্দুতে ধরা যায়।
\(F\) বলটি কোনো জড়বস্তুর \(A\) বিন্দুতে \(AX\) রেখা বরাবর ক্রিয়া করে। \(AX\) রেখার উপর তথা জড়বস্তুর উপর একটি বিন্দু \(B\) নেই। এখন \(B\) তে \(BA\) এবং \(BX\) বরাবর দুইটি সমান বল \(F\) প্রয়োগ করি। সমান ও বিপরীতমুখী বল প্রয়োগের ফলে বস্তুটির অবস্থানের কোনো পরিবর্তন হবে না।
এখন \(A\) বিন্দুতে \(AB\) বরবর কার্যরত \(F\) বল এবং \(B\) বিন্দুতে \(BA\) বরাবর কার্যরত \(F\) বল পরস্পর সমান ও বিপরীতমুখী হওয়ায় তারা একে অপরকে নিষ্ক্রিয় করবে।
সুতরাং বস্তুটির উপর একমাত্র কার্যরত বল হলো \(B\) বিন্দুতে \(BX\) বরাবর ক্রিয়ারত \(F\) বল। এই বলটি \(A\) বিন্দুতে \(AX\) বরাবর ক্রিয়ারত \(F\) বলের সমান। অতএব বলের ক্রিয়াবিন্দু বলের কার্যরেখার যেকোনো বিন্দুতে ধরা যায়।
মনে করি,
 \(F\) বলটি কোনো জড়বস্তুর \(A\) বিন্দুতে \(AX\) রেখা বরাবর ক্রিয়া করে। \(AX\) রেখার উপর তথা জড়বস্তুর উপর একটি বিন্দু \(B\) নেই। এখন \(B\) তে \(BA\) এবং \(BX\) বরাবর দুইটি সমান বল \(F\) প্রয়োগ করি। সমান ও বিপরীতমুখী বল প্রয়োগের ফলে বস্তুটির অবস্থানের কোনো পরিবর্তন হবে না।
এখন \(A\) বিন্দুতে \(AB\) বরবর কার্যরত \(F\) বল এবং \(B\) বিন্দুতে \(BA\) বরাবর কার্যরত \(F\) বল পরস্পর সমান ও বিপরীতমুখী হওয়ায় তারা একে অপরকে নিষ্ক্রিয় করবে।
সুতরাং বস্তুটির উপর একমাত্র কার্যরত বল হলো \(B\) বিন্দুতে \(BX\) বরাবর ক্রিয়ারত \(F\) বল। এই বলটি \(A\) বিন্দুতে \(AX\) বরাবর ক্রিয়ারত \(F\) বলের সমান। অতএব বলের ক্রিয়াবিন্দু বলের কার্যরেখার যেকোনো বিন্দুতে ধরা যায়।
\(F\) বলটি কোনো জড়বস্তুর \(A\) বিন্দুতে \(AX\) রেখা বরাবর ক্রিয়া করে। \(AX\) রেখার উপর তথা জড়বস্তুর উপর একটি বিন্দু \(B\) নেই। এখন \(B\) তে \(BA\) এবং \(BX\) বরাবর দুইটি সমান বল \(F\) প্রয়োগ করি। সমান ও বিপরীতমুখী বল প্রয়োগের ফলে বস্তুটির অবস্থানের কোনো পরিবর্তন হবে না।
এখন \(A\) বিন্দুতে \(AB\) বরবর কার্যরত \(F\) বল এবং \(B\) বিন্দুতে \(BA\) বরাবর কার্যরত \(F\) বল পরস্পর সমান ও বিপরীতমুখী হওয়ায় তারা একে অপরকে নিষ্ক্রিয় করবে।
সুতরাং বস্তুটির উপর একমাত্র কার্যরত বল হলো \(B\) বিন্দুতে \(BX\) বরাবর ক্রিয়ারত \(F\) বল। এই বলটি \(A\) বিন্দুতে \(AX\) বরাবর ক্রিয়ারত \(F\) বলের সমান। অতএব বলের ক্রিয়াবিন্দু বলের কার্যরেখার যেকোনো বিন্দুতে ধরা যায়।
বলের ক্রিয়া ও প্রতিক্রিয়া
Action and reaction of forces
যখন কোনো বস্তু অপর 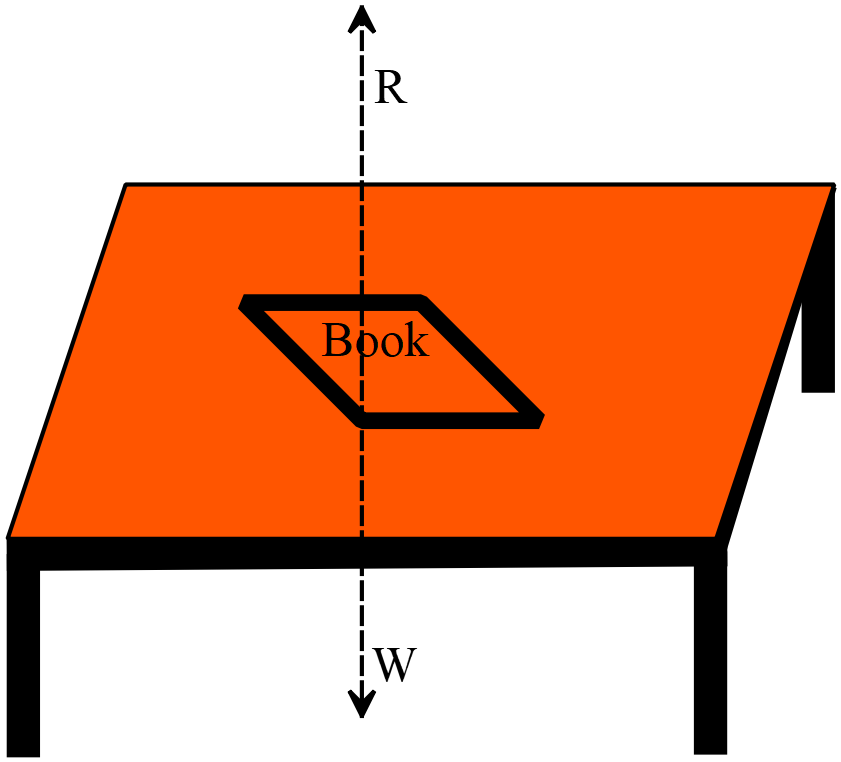 একটি বস্তুর উপর ঠেস দেওয়া অথবা একটি বস্তু অপর কোনো বস্তুর উপর রাখা হয় অথবা একটি বস্তু যখন অপর একটি বস্তুকে আঘাত করে তখন বস্তদ্বয়ের স্পর্শ বিন্দুতে উভয় বস্তুর উপরই একটি করে বল ক্রিয়া করে। প্রথম বস্তুটি দ্বিতীয় বস্তুর উপর যে বল প্রয়োগ করে তাকে ক্রিয়া এবং দ্বিতীয় বস্তুটি প্রথম বস্তুর উপর যে বল প্রয়োগ করে তাকে প্রতিক্রিয়া বলা হয়।
নিউটনের গতির তৃতীয় সূত্রানুসারে, ক্রিয়া ও প্রতিক্রিয়া বলদ্বয় সমান ও বিপরীতমুখী।
ক্রিয়া ও প্রতিক্রিয়া আরও স্পষ্টভাবে বোঝার জন্য পাশের চিত্রটি লক্ষ করিঃ
একটি টেবিলের উপর একটি বই রাখা আছে। এখানে বইটি টেবিলের উপর যে বল প্রয়োগ করেছে ঠিক সমপরিমাণ বল টেবিলও বইয়ের উপর প্রয়োগ করেছে। বই দ্বারা টেবিলে যে বল প্রয়োগ হয়েছে তাকে ক্রিয়া এবং টেবিল দ্বারা বইয়ের উপর যে বল প্রয়োগ হয়েছে তাকে প্রতিক্রিয়া বলা হয়। এখানে উভয় বলই বই ও টেবিলের সাথে পরস্পর লম্ব।
একটি বস্তুর উপর ঠেস দেওয়া অথবা একটি বস্তু অপর কোনো বস্তুর উপর রাখা হয় অথবা একটি বস্তু যখন অপর একটি বস্তুকে আঘাত করে তখন বস্তদ্বয়ের স্পর্শ বিন্দুতে উভয় বস্তুর উপরই একটি করে বল ক্রিয়া করে। প্রথম বস্তুটি দ্বিতীয় বস্তুর উপর যে বল প্রয়োগ করে তাকে ক্রিয়া এবং দ্বিতীয় বস্তুটি প্রথম বস্তুর উপর যে বল প্রয়োগ করে তাকে প্রতিক্রিয়া বলা হয়।
নিউটনের গতির তৃতীয় সূত্রানুসারে, ক্রিয়া ও প্রতিক্রিয়া বলদ্বয় সমান ও বিপরীতমুখী।
ক্রিয়া ও প্রতিক্রিয়া আরও স্পষ্টভাবে বোঝার জন্য পাশের চিত্রটি লক্ষ করিঃ
একটি টেবিলের উপর একটি বই রাখা আছে। এখানে বইটি টেবিলের উপর যে বল প্রয়োগ করেছে ঠিক সমপরিমাণ বল টেবিলও বইয়ের উপর প্রয়োগ করেছে। বই দ্বারা টেবিলে যে বল প্রয়োগ হয়েছে তাকে ক্রিয়া এবং টেবিল দ্বারা বইয়ের উপর যে বল প্রয়োগ হয়েছে তাকে প্রতিক্রিয়া বলা হয়। এখানে উভয় বলই বই ও টেবিলের সাথে পরস্পর লম্ব।
 একটি বস্তুর উপর ঠেস দেওয়া অথবা একটি বস্তু অপর কোনো বস্তুর উপর রাখা হয় অথবা একটি বস্তু যখন অপর একটি বস্তুকে আঘাত করে তখন বস্তদ্বয়ের স্পর্শ বিন্দুতে উভয় বস্তুর উপরই একটি করে বল ক্রিয়া করে। প্রথম বস্তুটি দ্বিতীয় বস্তুর উপর যে বল প্রয়োগ করে তাকে ক্রিয়া এবং দ্বিতীয় বস্তুটি প্রথম বস্তুর উপর যে বল প্রয়োগ করে তাকে প্রতিক্রিয়া বলা হয়।
নিউটনের গতির তৃতীয় সূত্রানুসারে, ক্রিয়া ও প্রতিক্রিয়া বলদ্বয় সমান ও বিপরীতমুখী।
ক্রিয়া ও প্রতিক্রিয়া আরও স্পষ্টভাবে বোঝার জন্য পাশের চিত্রটি লক্ষ করিঃ
একটি টেবিলের উপর একটি বই রাখা আছে। এখানে বইটি টেবিলের উপর যে বল প্রয়োগ করেছে ঠিক সমপরিমাণ বল টেবিলও বইয়ের উপর প্রয়োগ করেছে। বই দ্বারা টেবিলে যে বল প্রয়োগ হয়েছে তাকে ক্রিয়া এবং টেবিল দ্বারা বইয়ের উপর যে বল প্রয়োগ হয়েছে তাকে প্রতিক্রিয়া বলা হয়। এখানে উভয় বলই বই ও টেবিলের সাথে পরস্পর লম্ব।
একটি বস্তুর উপর ঠেস দেওয়া অথবা একটি বস্তু অপর কোনো বস্তুর উপর রাখা হয় অথবা একটি বস্তু যখন অপর একটি বস্তুকে আঘাত করে তখন বস্তদ্বয়ের স্পর্শ বিন্দুতে উভয় বস্তুর উপরই একটি করে বল ক্রিয়া করে। প্রথম বস্তুটি দ্বিতীয় বস্তুর উপর যে বল প্রয়োগ করে তাকে ক্রিয়া এবং দ্বিতীয় বস্তুটি প্রথম বস্তুর উপর যে বল প্রয়োগ করে তাকে প্রতিক্রিয়া বলা হয়।
নিউটনের গতির তৃতীয় সূত্রানুসারে, ক্রিয়া ও প্রতিক্রিয়া বলদ্বয় সমান ও বিপরীতমুখী।
ক্রিয়া ও প্রতিক্রিয়া আরও স্পষ্টভাবে বোঝার জন্য পাশের চিত্রটি লক্ষ করিঃ
একটি টেবিলের উপর একটি বই রাখা আছে। এখানে বইটি টেবিলের উপর যে বল প্রয়োগ করেছে ঠিক সমপরিমাণ বল টেবিলও বইয়ের উপর প্রয়োগ করেছে। বই দ্বারা টেবিলে যে বল প্রয়োগ হয়েছে তাকে ক্রিয়া এবং টেবিল দ্বারা বইয়ের উপর যে বল প্রয়োগ হয়েছে তাকে প্রতিক্রিয়া বলা হয়। এখানে উভয় বলই বই ও টেবিলের সাথে পরস্পর লম্ব।
বিভিন্ন প্রকারের বল
Different kinds of forces
উৎস ও প্রয়োগ ক্ষেত্রের উপর ভিত্তি করে বলকে বিভিন্ন নামে নামকরণ করা হয়েছে।
যেমনঃ
টান ও উর্ধ্বচাপ
Tension and Overpressure
টানঃ 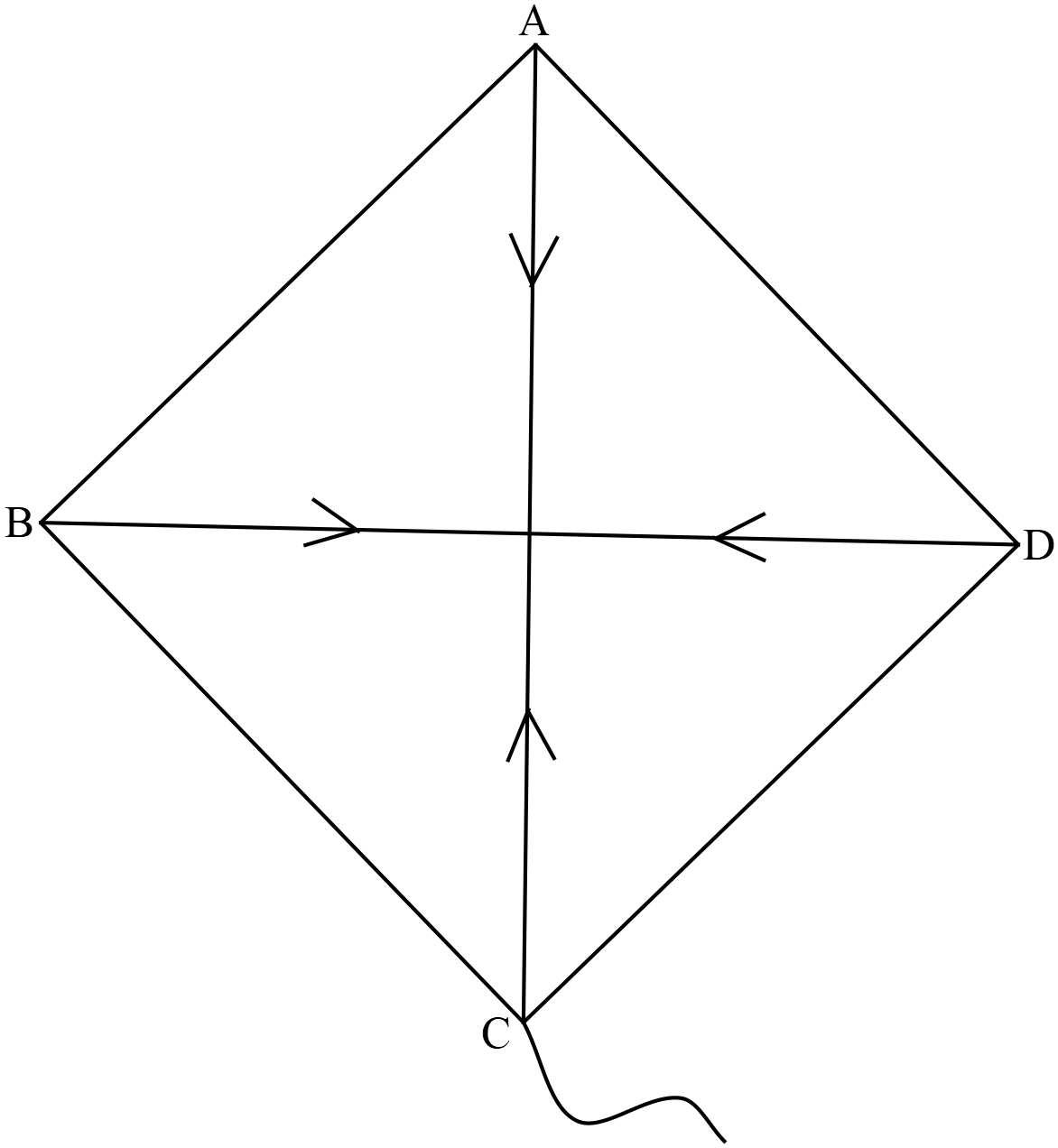 কোনো বস্তুকে একটি সরু রশি বা তার দ্বারা টানা হলে ঐ রশি বা তার বরাবর বস্তুটির উপর যে বল ক্রিয়া করে তাকে টান বলা হয়।
চিত্রে \(AC\) ও \(BD\) বরাবর সুতা দিয়ে আটকিয়ে \(AB,BC,CD\) ও \(DA\) কাটি চারটি দ্বারা \(ABCD\) ঘুড়ি তৈরি করা হয়েছে। এখানে \(AC\) ও \(BD\) বরাবর টান ক্রিয়াশীল এবং সুতার টান '\(\rightarrow\)' চিহ্নিত দিক বরাবর ক্রিয়াশীল।
কোনো বস্তুকে একটি সরু রশি বা তার দ্বারা টানা হলে ঐ রশি বা তার বরাবর বস্তুটির উপর যে বল ক্রিয়া করে তাকে টান বলা হয়।
চিত্রে \(AC\) ও \(BD\) বরাবর সুতা দিয়ে আটকিয়ে \(AB,BC,CD\) ও \(DA\) কাটি চারটি দ্বারা \(ABCD\) ঘুড়ি তৈরি করা হয়েছে। এখানে \(AC\) ও \(BD\) বরাবর টান ক্রিয়াশীল এবং সুতার টান '\(\rightarrow\)' চিহ্নিত দিক বরাবর ক্রিয়াশীল।
 কোনো বস্তুকে একটি সরু রশি বা তার দ্বারা টানা হলে ঐ রশি বা তার বরাবর বস্তুটির উপর যে বল ক্রিয়া করে তাকে টান বলা হয়।
চিত্রে \(AC\) ও \(BD\) বরাবর সুতা দিয়ে আটকিয়ে \(AB,BC,CD\) ও \(DA\) কাটি চারটি দ্বারা \(ABCD\) ঘুড়ি তৈরি করা হয়েছে। এখানে \(AC\) ও \(BD\) বরাবর টান ক্রিয়াশীল এবং সুতার টান '\(\rightarrow\)' চিহ্নিত দিক বরাবর ক্রিয়াশীল।
কোনো বস্তুকে একটি সরু রশি বা তার দ্বারা টানা হলে ঐ রশি বা তার বরাবর বস্তুটির উপর যে বল ক্রিয়া করে তাকে টান বলা হয়।
চিত্রে \(AC\) ও \(BD\) বরাবর সুতা দিয়ে আটকিয়ে \(AB,BC,CD\) ও \(DA\) কাটি চারটি দ্বারা \(ABCD\) ঘুড়ি তৈরি করা হয়েছে। এখানে \(AC\) ও \(BD\) বরাবর টান ক্রিয়াশীল এবং সুতার টান '\(\rightarrow\)' চিহ্নিত দিক বরাবর ক্রিয়াশীল।
চাপ
Pressure
চাপঃ যখন একটি বস্তুকে অপর একটি বস্তুর উপর রাখা হয়, তখন প্রথম বস্তুটি দ্বিতীয় বস্তুর উপর যে বল প্রয়োগ করে তাকে চাপ বলা হয়।
ঠেলা
Push
ঠেলাঃ অনেক সময় দেখা যায় বাস (বা অন্য কোনো গাড়ী) কোনো স্থানে রাখা ছিল, এখন স্টার্ট দেওয়ার সময় স্টার্ট নিচ্ছে না। এমতাবস্থায় বাস্টিকে কতকগুলি লোক বল প্রয়োগে সামনে বা পিছনে সরানোর চেষ্টা করে এবং একটু গড়ালেই ড্রাইভার স্টার্ট করতে সক্ষম হন। এই ক্ষেত্রে যে বল প্রয়োগে গাড়ীকে গড়ানো হয় তাকে ঠেলা বা ধাক্কা বলা হয়।
ঘর্ষণ
Friction
ঘর্ষণঃ একটি বস্তু অপর একটি বস্তুর উপর দিয়ে ( স্পর্শ করে ) চলতে গেলে বাধাপ্রাপ্ত হয়। ফুটবলে শট দিলে তা কিছুক্ষণ ভূমিতে গড়ানোর পরে থেমে যাবে। ফুটবলটি নিশ্চয়ই কোনো বাধার কারণে থামে গেছে। এখানে ভূমির সংস্পর্শে গড়ানোর কারণে যে বল বাধা হিসেবে কাজ করে তাকে ঘর্ষণ বল এবং যে বিন্দুতে স্পর্শ করে ঐ বিন্দুকে ঘর্ষণ বিন্দু বলা হয়।
আকর্ষণ
Attraction
আকর্ষণঃ বাহ্যিক কোনো বল ( চাপ, ঠেলা, ধাক্কা ) প্রয়োগ ব্যতিরেকে একে অপরকে স্পর্শ করেনি এরূপ দুইটি বস্তু যে বলের ক্রিয়ার কারণে একে অপরের দিকে অথবা যে কোনো একটি অপরটির দিকে অগ্রসর হয় বা হওয়ার প্রবণতা সৃষ্টি হয় তাকে আকর্ষণ বল বলা হয়।
যেমনঃ একটি লৌহ খন্ড চুম্বকের আকর্ষণে চুম্বকের দিকে অগ্রসর হয়, পৃথিবীর আকর্ষণে বৃন্তচ্যুত ফল মাটিতে পড়ে।
বিকর্ষণ
Repulsion
বিকর্ষণঃ বাহ্যিক কোনো বল ( চাপ, ঠেলা, ধাক্কা ) প্রয়োগ ব্যতিরেকে একে অপরকে স্পর্শ করেনি এরূপ দুইটি বস্তু যে বলের ক্রিয়ার ফলে একটি অন্যটি থেকে সরে যায়, তাকে বিকর্ষণ বল বলা হয়।
যেমনঃ চুম্বকের সমজাতীয় দুই মেরু কছাকাছি আনলে চুম্বকদ্বয় পরস্পর হতে দূরে সরে যাবে। একে বিকর্ষণ বলা হয়।
ওজন
Weight
ওজনঃ কোনো বস্তুকে পৃথিবী তার কেন্দ্রের দিকে যে পরিমাণ আকর্ষণ বল দ্বারা টানে তাকে ঐ বস্তুর ওজন বলা হয়। বস্তুর ওজন সর্বদা বস্তুর উপরোস্থ একটি নির্দিষ্ট বিন্দু দিয়ে খাড়া নিচের দিকে ক্রিয়াশীল। ঐ নির্দিষ্ট বিন্দুটিকে বস্তুর ভরকেন্দ্র বলা হয়।
অন্তকেন্দ্র
Inner centre
অন্তকেন্দ্রঃ 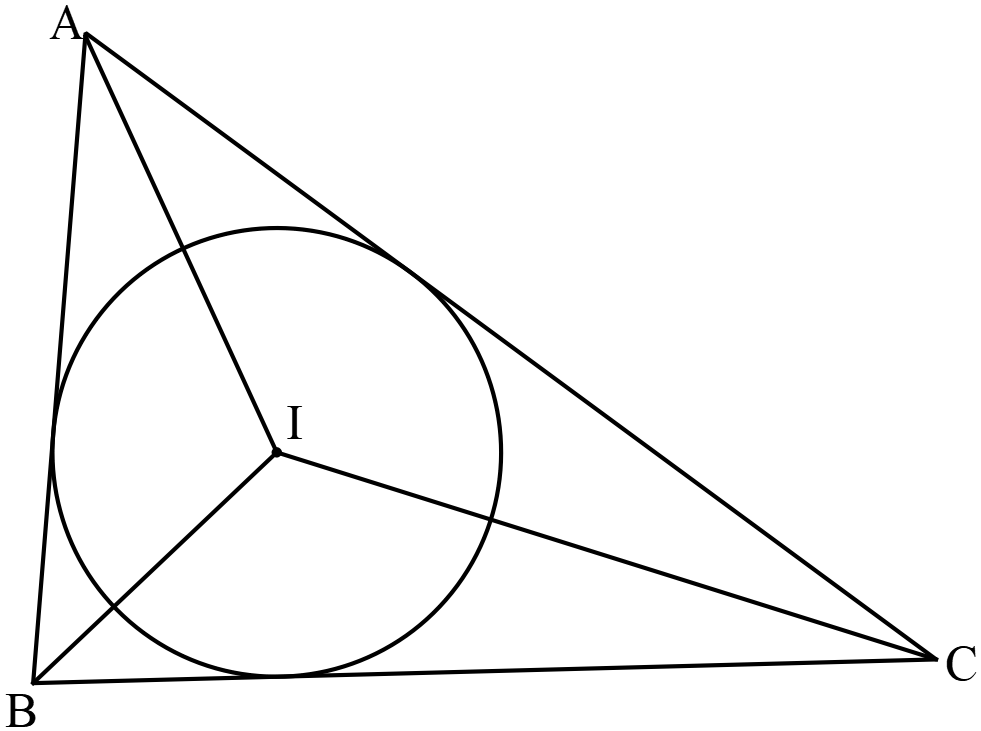 ত্রিভুজের অন্তঃস্থ কোণত্রয়ের সমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের অন্তঃকেন্দ্র বলা হয়। অন্তঃকেন্দ্র হলো ত্রিভুজে অন্তর্লিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের অন্তঃকেন্দ্র \(I\) । কেননা \(IA,IB,IC\) যথাক্রমে \(A,B\) ও \(C\) কোণকে সমদ্বিখন্ডিত করে।
ত্রিভুজের অন্তঃস্থ কোণত্রয়ের সমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের অন্তঃকেন্দ্র বলা হয়। অন্তঃকেন্দ্র হলো ত্রিভুজে অন্তর্লিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের অন্তঃকেন্দ্র \(I\) । কেননা \(IA,IB,IC\) যথাক্রমে \(A,B\) ও \(C\) কোণকে সমদ্বিখন্ডিত করে।
 ত্রিভুজের অন্তঃস্থ কোণত্রয়ের সমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের অন্তঃকেন্দ্র বলা হয়। অন্তঃকেন্দ্র হলো ত্রিভুজে অন্তর্লিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের অন্তঃকেন্দ্র \(I\) । কেননা \(IA,IB,IC\) যথাক্রমে \(A,B\) ও \(C\) কোণকে সমদ্বিখন্ডিত করে।
ত্রিভুজের অন্তঃস্থ কোণত্রয়ের সমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের অন্তঃকেন্দ্র বলা হয়। অন্তঃকেন্দ্র হলো ত্রিভুজে অন্তর্লিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের অন্তঃকেন্দ্র \(I\) । কেননা \(IA,IB,IC\) যথাক্রমে \(A,B\) ও \(C\) কোণকে সমদ্বিখন্ডিত করে।
পরিকেন্দ্র
Circumcentre
পরিকেন্দ্রঃ 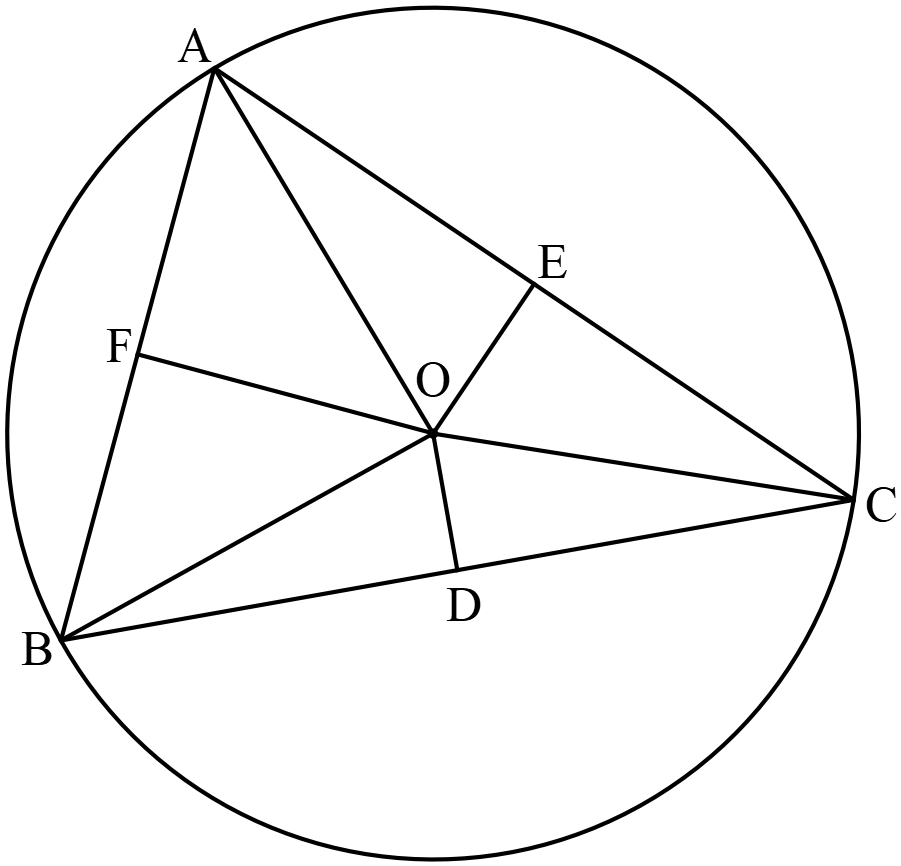 ত্রিভুজের বাহুত্রয়ের লম্বসমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের পরিকেন্দ্র বলা হয়। পরিকেন্দ্র হলো ত্রিভুজের পরিলিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের পরিকেন্দ্র \(O;\) \(A, B, C\) বিন্দু হতে সমদূরবর্তী । \(OA=OB=OC\) এবং \(OD, OE, OF\) যথাক্রমে \(BC, CA, AB\) বাহুত্রয়ের লম্বদ্বিখন্ডক।
ত্রিভুজের বাহুত্রয়ের লম্বসমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের পরিকেন্দ্র বলা হয়। পরিকেন্দ্র হলো ত্রিভুজের পরিলিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের পরিকেন্দ্র \(O;\) \(A, B, C\) বিন্দু হতে সমদূরবর্তী । \(OA=OB=OC\) এবং \(OD, OE, OF\) যথাক্রমে \(BC, CA, AB\) বাহুত্রয়ের লম্বদ্বিখন্ডক।
 ত্রিভুজের বাহুত্রয়ের লম্বসমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের পরিকেন্দ্র বলা হয়। পরিকেন্দ্র হলো ত্রিভুজের পরিলিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের পরিকেন্দ্র \(O;\) \(A, B, C\) বিন্দু হতে সমদূরবর্তী । \(OA=OB=OC\) এবং \(OD, OE, OF\) যথাক্রমে \(BC, CA, AB\) বাহুত্রয়ের লম্বদ্বিখন্ডক।
ত্রিভুজের বাহুত্রয়ের লম্বসমদ্বিখন্ডকত্রয়ের ছেদবিন্দুকে ত্রিভুজের পরিকেন্দ্র বলা হয়। পরিকেন্দ্র হলো ত্রিভুজের পরিলিখিত বৃত্তের কেন্দ্র।
চিত্রে \(ABC\) ত্রিভুজের পরিকেন্দ্র \(O;\) \(A, B, C\) বিন্দু হতে সমদূরবর্তী । \(OA=OB=OC\) এবং \(OD, OE, OF\) যথাক্রমে \(BC, CA, AB\) বাহুত্রয়ের লম্বদ্বিখন্ডক।
ভরকেন্দ্র
Centroid
ভরকেন্দ্রঃ 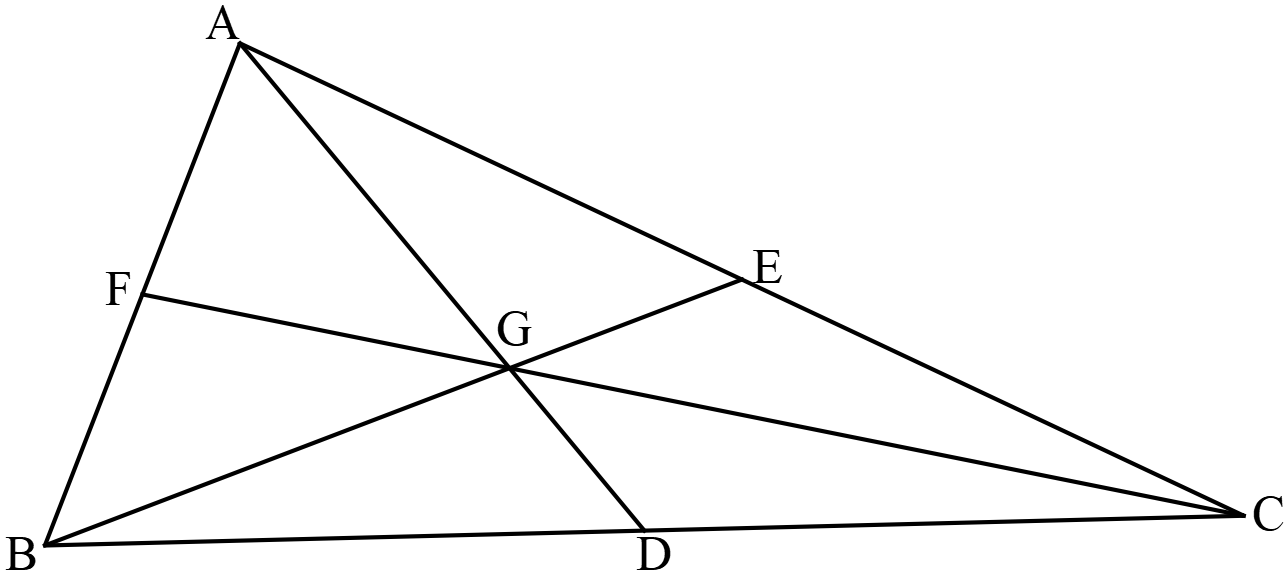 কোনো ত্রিভুজের মধ্যমাত্রয়ের ছেদবিন্দুকে ত্রিভুজের ভরকেন্দ্র বলা হয়। ভরকেন্দ্র প্রতিটি মধ্যমাকেই \(2:1\) অনুপাতে বিভক্ত করে।
চিত্রে \(ABC\) ত্রিভুজের ভরকেন্দ্র \(G\)। \(AD, BE\) ও \(CF\) মধ্যমা।
কোনো ত্রিভুজের মধ্যমাত্রয়ের ছেদবিন্দুকে ত্রিভুজের ভরকেন্দ্র বলা হয়। ভরকেন্দ্র প্রতিটি মধ্যমাকেই \(2:1\) অনুপাতে বিভক্ত করে।
চিত্রে \(ABC\) ত্রিভুজের ভরকেন্দ্র \(G\)। \(AD, BE\) ও \(CF\) মধ্যমা।
 কোনো ত্রিভুজের মধ্যমাত্রয়ের ছেদবিন্দুকে ত্রিভুজের ভরকেন্দ্র বলা হয়। ভরকেন্দ্র প্রতিটি মধ্যমাকেই \(2:1\) অনুপাতে বিভক্ত করে।
চিত্রে \(ABC\) ত্রিভুজের ভরকেন্দ্র \(G\)। \(AD, BE\) ও \(CF\) মধ্যমা।
কোনো ত্রিভুজের মধ্যমাত্রয়ের ছেদবিন্দুকে ত্রিভুজের ভরকেন্দ্র বলা হয়। ভরকেন্দ্র প্রতিটি মধ্যমাকেই \(2:1\) অনুপাতে বিভক্ত করে।
চিত্রে \(ABC\) ত্রিভুজের ভরকেন্দ্র \(G\)। \(AD, BE\) ও \(CF\) মধ্যমা।
লম্বকেন্দ্র
Orthocentre
লম্বকেন্দ্রঃ 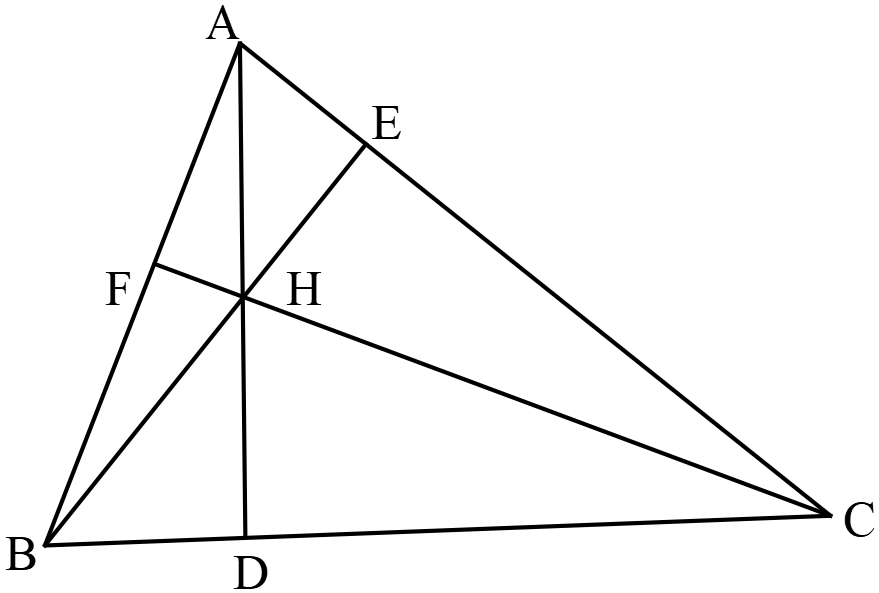 কোনো ত্রিভুজের শীর্ষবিন্দুত্রয় হতে বিপরীত বাহুর ওপর অঙ্কিত লম্বত্রয়ের ছেদবিন্দুকে ত্রিভুজের লম্বকেন্দ্র বলা হয়।
চিত্রে \(ABC\) ত্রিভুজের লম্বকেন্দ্র \(H\)। \(AD, BE\) ও \(CF\) যথাক্রমে \(BC, CA\) ও \(AB\) বাহুগুলির ওপর বিপরীত শীর্ষগুলি হতে অঙ্কিত লম্ব।
কোনো ত্রিভুজের শীর্ষবিন্দুত্রয় হতে বিপরীত বাহুর ওপর অঙ্কিত লম্বত্রয়ের ছেদবিন্দুকে ত্রিভুজের লম্বকেন্দ্র বলা হয়।
চিত্রে \(ABC\) ত্রিভুজের লম্বকেন্দ্র \(H\)। \(AD, BE\) ও \(CF\) যথাক্রমে \(BC, CA\) ও \(AB\) বাহুগুলির ওপর বিপরীত শীর্ষগুলি হতে অঙ্কিত লম্ব।
 কোনো ত্রিভুজের শীর্ষবিন্দুত্রয় হতে বিপরীত বাহুর ওপর অঙ্কিত লম্বত্রয়ের ছেদবিন্দুকে ত্রিভুজের লম্বকেন্দ্র বলা হয়।
চিত্রে \(ABC\) ত্রিভুজের লম্বকেন্দ্র \(H\)। \(AD, BE\) ও \(CF\) যথাক্রমে \(BC, CA\) ও \(AB\) বাহুগুলির ওপর বিপরীত শীর্ষগুলি হতে অঙ্কিত লম্ব।
কোনো ত্রিভুজের শীর্ষবিন্দুত্রয় হতে বিপরীত বাহুর ওপর অঙ্কিত লম্বত্রয়ের ছেদবিন্দুকে ত্রিভুজের লম্বকেন্দ্র বলা হয়।
চিত্রে \(ABC\) ত্রিভুজের লম্বকেন্দ্র \(H\)। \(AD, BE\) ও \(CF\) যথাক্রমে \(BC, CA\) ও \(AB\) বাহুগুলির ওপর বিপরীত শীর্ষগুলি হতে অঙ্কিত লম্ব।
দুইটি বলের লব্ধি
Resultant of two forces
একই সময়ে কোনো বস্তুকণার উপর 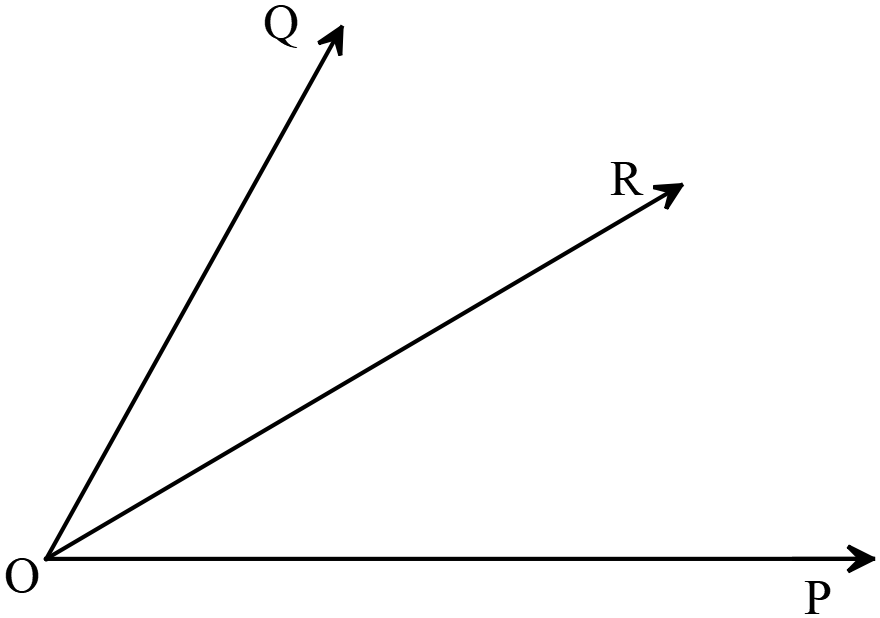 দুইটি বল প্রযুক্ত হলে, এই বলদ্বয়ের সম্মিলিত ক্রিয়াফল যদি বস্তু কণাটির উপর নির্দিষ্ট দিকে একটি মাত্র বলের ক্রিয়াফলের সমান হয়, তবে ঐ এক মাত্র বলকে প্রযুক্ত বল দুইটির লব্ধি বল বলে।
চিত্রে \(O\) একটি বস্তুকণা এবং \(O\) তে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) এর সম্মিলিত ক্রিয়াফল অপর বল \(R\) এর সমান হলে, \(R\) বলকে \(P\) ও \(Q\) বল দুইটির লব্ধি বলে।
দুইটি বল প্রযুক্ত হলে, এই বলদ্বয়ের সম্মিলিত ক্রিয়াফল যদি বস্তু কণাটির উপর নির্দিষ্ট দিকে একটি মাত্র বলের ক্রিয়াফলের সমান হয়, তবে ঐ এক মাত্র বলকে প্রযুক্ত বল দুইটির লব্ধি বল বলে।
চিত্রে \(O\) একটি বস্তুকণা এবং \(O\) তে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) এর সম্মিলিত ক্রিয়াফল অপর বল \(R\) এর সমান হলে, \(R\) বলকে \(P\) ও \(Q\) বল দুইটির লব্ধি বলে।
যেমনঃ দুর্ঘটনাবশত একটি রেলগাড়ী লাইনচ্যুত হয়ে পার্শে পড়ে আছে। এই গাড়ীখানা লাইনের উপরে উঠানোর জন্য কোনো রিলিফ ট্রেনের দুইটি ক্রেন একত্রে ব্যবহার করতে হয়। কিন্তু অন্য আর একটি রিলিফ ট্রেন আছে যার একটি ক্রেন ব্যবহার করেই ঐ রেলগাড়ীটি লাইনের উপরে উঠানো যায়। এখানে পূর্বোক্ত ক্রেন দুইটির লব্ধি বল হলো পরবর্তী একটি ক্রেনের বল।
 দুইটি বল প্রযুক্ত হলে, এই বলদ্বয়ের সম্মিলিত ক্রিয়াফল যদি বস্তু কণাটির উপর নির্দিষ্ট দিকে একটি মাত্র বলের ক্রিয়াফলের সমান হয়, তবে ঐ এক মাত্র বলকে প্রযুক্ত বল দুইটির লব্ধি বল বলে।
চিত্রে \(O\) একটি বস্তুকণা এবং \(O\) তে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) এর সম্মিলিত ক্রিয়াফল অপর বল \(R\) এর সমান হলে, \(R\) বলকে \(P\) ও \(Q\) বল দুইটির লব্ধি বলে।
দুইটি বল প্রযুক্ত হলে, এই বলদ্বয়ের সম্মিলিত ক্রিয়াফল যদি বস্তু কণাটির উপর নির্দিষ্ট দিকে একটি মাত্র বলের ক্রিয়াফলের সমান হয়, তবে ঐ এক মাত্র বলকে প্রযুক্ত বল দুইটির লব্ধি বল বলে।
চিত্রে \(O\) একটি বস্তুকণা এবং \(O\) তে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) এর সম্মিলিত ক্রিয়াফল অপর বল \(R\) এর সমান হলে, \(R\) বলকে \(P\) ও \(Q\) বল দুইটির লব্ধি বলে। যেমনঃ দুর্ঘটনাবশত একটি রেলগাড়ী লাইনচ্যুত হয়ে পার্শে পড়ে আছে। এই গাড়ীখানা লাইনের উপরে উঠানোর জন্য কোনো রিলিফ ট্রেনের দুইটি ক্রেন একত্রে ব্যবহার করতে হয়। কিন্তু অন্য আর একটি রিলিফ ট্রেন আছে যার একটি ক্রেন ব্যবহার করেই ঐ রেলগাড়ীটি লাইনের উপরে উঠানো যায়। এখানে পূর্বোক্ত ক্রেন দুইটির লব্ধি বল হলো পরবর্তী একটি ক্রেনের বল।
দুইটি বলের লব্ধির মাণ ও দিক
Magnitude and direction Of resultant of two forcess
একই সরলরেখায় একই দিকে ক্রিয়াশীল দুইটি বলের  লব্ধির মাণ হবে বলদ্বয়ের সমষ্টির সমান এবং দিক হবে বলদ্বয়ের দিক বরাবর।
লব্ধির মাণ হবে বলদ্বয়ের সমষ্টির সমান এবং দিক হবে বলদ্বয়ের দিক বরাবর।
আবার একই সরলরেখায় বিপরীত দিকে ক্রিয়াশীল দুইটি বলের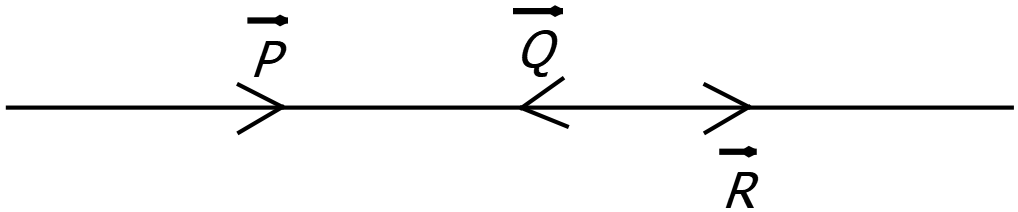 লব্ধির মাণ হবে বলদ্বয়ের অন্তর ফলের সমান এবং দিক হবে বৃহত্তর বলের দিক বরাবর।
লব্ধির মাণ হবে বলদ্বয়ের অন্তর ফলের সমান এবং দিক হবে বৃহত্তর বলের দিক বরাবর।
১ম চিত্রানুসারে , \(P\) ও \(Q\) বলদ্বয়ের লব্ধি \(R\) হলে, \(R=P+Q\) এবং দিক হবে প্রদত্ত \(P\) ও \(Q\) এর দিক।
২য় চিত্রানুসারে , \(P\) ও \(Q\) বলদ্বয়ের লব্ধি \(R\) এবং \(P>Q\) হলে, \(R=P-Q\) এবং দিক হবে \(P\) এর দিক।
আবার, \(Q>P\) হলে, \(R=Q-P\) এবং দিক হবে \(Q\) এর দিক।
কোনো বস্তুর একটি বিন্দুতে দুইটি বল একই সময়ে ভিন্ন ভিন্ন দিকে ক্রিয়াশীল হলে তাদের লব্ধি "বলের সামান্তরিক সূত্রের " দ্বারা নির্ণয় করা হয়।
 লব্ধির মাণ হবে বলদ্বয়ের সমষ্টির সমান এবং দিক হবে বলদ্বয়ের দিক বরাবর।
লব্ধির মাণ হবে বলদ্বয়ের সমষ্টির সমান এবং দিক হবে বলদ্বয়ের দিক বরাবর। আবার একই সরলরেখায় বিপরীত দিকে ক্রিয়াশীল দুইটি বলের
 লব্ধির মাণ হবে বলদ্বয়ের অন্তর ফলের সমান এবং দিক হবে বৃহত্তর বলের দিক বরাবর।
লব্ধির মাণ হবে বলদ্বয়ের অন্তর ফলের সমান এবং দিক হবে বৃহত্তর বলের দিক বরাবর। ১ম চিত্রানুসারে , \(P\) ও \(Q\) বলদ্বয়ের লব্ধি \(R\) হলে, \(R=P+Q\) এবং দিক হবে প্রদত্ত \(P\) ও \(Q\) এর দিক।
২য় চিত্রানুসারে , \(P\) ও \(Q\) বলদ্বয়ের লব্ধি \(R\) এবং \(P>Q\) হলে, \(R=P-Q\) এবং দিক হবে \(P\) এর দিক।
আবার, \(Q>P\) হলে, \(R=Q-P\) এবং দিক হবে \(Q\) এর দিক।
কোনো বস্তুর একটি বিন্দুতে দুইটি বল একই সময়ে ভিন্ন ভিন্ন দিকে ক্রিয়াশীল হলে তাদের লব্ধি "বলের সামান্তরিক সূত্রের " দ্বারা নির্ণয় করা হয়।
বলের সামান্তরিক সূত্র
Parallelogram law of forces
বর্ণনাঃ যদি কোন সামান্তরিকের দুইটি সন্নিহিত বাহু দ্বারা কোন বিন্দুতে একই সময়ে ক্রিয়ারত দুইটি বলের মান ও দিক সূচিত করা যায়, তাহলে সামান্তরিকের উক্ত বাহুদ্বয়ের ছেদবিন্দুগামী কর্ণ দ্বারা উক্ত বলদ্বয়ের লব্ধির মান ও দিক সূচিত হয়।
ব্যাখ্যাঃ মনে করি \(OABC\) সামান্তরিকের \(O\) বিন্দুতে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) যথাক্রমে সন্নিহিত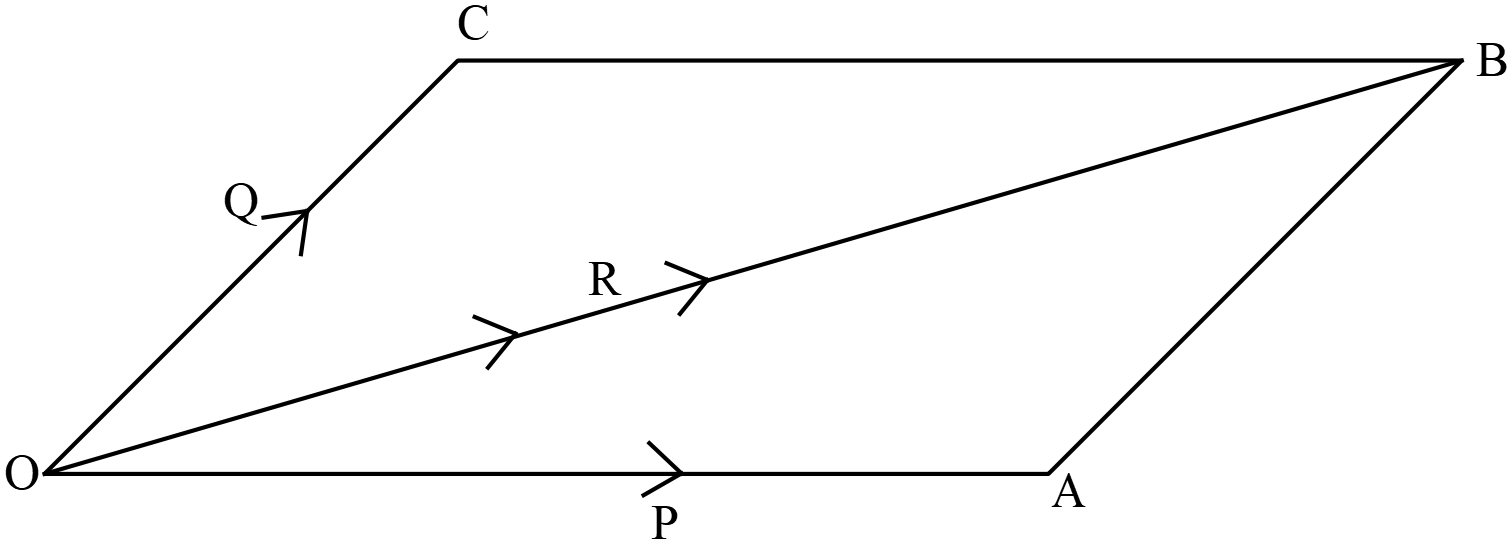 বাহু \(OA\) ও \(OC\) দ্বারা সূচিত।
অর্থাৎ ভেক্টর সূচকে প্রকাশ করলে \(\overrightarrow{OA}=P\) এবং \(\overrightarrow{OC}=Q\) এখানে \(P\) ও \(Q\) উভয়ে ভেক্টর রাশি। সুতরাং ভেক্টর যোজনের সামান্তরিক বিধি অনুসারে তাদের যোগফল বা লব্ধি সামান্তরিক \(OABC\) এর কর্ণ \(OB\) দ্বারা সূচিত হবে। ধরি, \(P\) ও \(Q\) এর লব্ধি \(R\) তাহলে \(R\) এর মাণ ও দিক কর্ণ \(OB\) দ্বারা সূচিত হবে।
বাহু \(OA\) ও \(OC\) দ্বারা সূচিত।
অর্থাৎ ভেক্টর সূচকে প্রকাশ করলে \(\overrightarrow{OA}=P\) এবং \(\overrightarrow{OC}=Q\) এখানে \(P\) ও \(Q\) উভয়ে ভেক্টর রাশি। সুতরাং ভেক্টর যোজনের সামান্তরিক বিধি অনুসারে তাদের যোগফল বা লব্ধি সামান্তরিক \(OABC\) এর কর্ণ \(OB\) দ্বারা সূচিত হবে। ধরি, \(P\) ও \(Q\) এর লব্ধি \(R\) তাহলে \(R\) এর মাণ ও দিক কর্ণ \(OB\) দ্বারা সূচিত হবে।
ভেক্টর সূচকে প্রকাশ করলে পাই, \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}\) অর্থাৎ \(P+Q=R\)
বিঃদ্রঃ বলের এককসহ \(P, \ Q\) ও \(R\) বল তিনটিকে দৈর্ঘ্যের এককসহ যথাক্রমে \(OA, \ OB\) ও \(OC\) রেখাংশ দ্বারা সূচিত করা যায়।
যদি, \(\frac{OA}{P}=\frac{OB}{Q}=\frac{OC}{R}\) হয়।
\(OA\equiv{P}\) বা \(\overline{OA}=\bar{P}\) দ্বারা আমরা বুঝি যে, \(OA, \ P\) বলকে প্রকাশ করে।
\(OA=P\) এর অর্থ \(P\) বলটি \(OA\) অথবা এর সমান্তরাল বরাবর ক্রিয়ারত।
ব্যাখ্যাঃ মনে করি \(OABC\) সামান্তরিকের \(O\) বিন্দুতে ক্রিয়ারত দুইটি বল \(P\) ও \(Q\) যথাক্রমে সন্নিহিত
 বাহু \(OA\) ও \(OC\) দ্বারা সূচিত।
অর্থাৎ ভেক্টর সূচকে প্রকাশ করলে \(\overrightarrow{OA}=P\) এবং \(\overrightarrow{OC}=Q\) এখানে \(P\) ও \(Q\) উভয়ে ভেক্টর রাশি। সুতরাং ভেক্টর যোজনের সামান্তরিক বিধি অনুসারে তাদের যোগফল বা লব্ধি সামান্তরিক \(OABC\) এর কর্ণ \(OB\) দ্বারা সূচিত হবে। ধরি, \(P\) ও \(Q\) এর লব্ধি \(R\) তাহলে \(R\) এর মাণ ও দিক কর্ণ \(OB\) দ্বারা সূচিত হবে।
বাহু \(OA\) ও \(OC\) দ্বারা সূচিত।
অর্থাৎ ভেক্টর সূচকে প্রকাশ করলে \(\overrightarrow{OA}=P\) এবং \(\overrightarrow{OC}=Q\) এখানে \(P\) ও \(Q\) উভয়ে ভেক্টর রাশি। সুতরাং ভেক্টর যোজনের সামান্তরিক বিধি অনুসারে তাদের যোগফল বা লব্ধি সামান্তরিক \(OABC\) এর কর্ণ \(OB\) দ্বারা সূচিত হবে। ধরি, \(P\) ও \(Q\) এর লব্ধি \(R\) তাহলে \(R\) এর মাণ ও দিক কর্ণ \(OB\) দ্বারা সূচিত হবে।ভেক্টর সূচকে প্রকাশ করলে পাই, \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}\) অর্থাৎ \(P+Q=R\)
বিঃদ্রঃ বলের এককসহ \(P, \ Q\) ও \(R\) বল তিনটিকে দৈর্ঘ্যের এককসহ যথাক্রমে \(OA, \ OB\) ও \(OC\) রেখাংশ দ্বারা সূচিত করা যায়।
যদি, \(\frac{OA}{P}=\frac{OB}{Q}=\frac{OC}{R}\) হয়।
\(OA\equiv{P}\) বা \(\overline{OA}=\bar{P}\) দ্বারা আমরা বুঝি যে, \(OA, \ P\) বলকে প্রকাশ করে।
\(OA=P\) এর অর্থ \(P\) বলটি \(OA\) অথবা এর সমান্তরাল বরাবর ক্রিয়ারত।
বলবিদ্যায় ব্যবহৃত কয়েকটি প্রয়োজনীয় উপপাদ্য ও তার প্রমাণ
Some essential theorems used in mechanics and their proofs
বল সামান্তরিক সুত্রটি লিখ এবং এক বিন্দুতে পরস্পর \(\alpha\) কোণে ক্রিয়ারত দুইটি বলের লব্ধির মান ও দিক নির্ণয় কর।
উত্তরঃ লব্ধির মান \(R=\sqrt{P^{2}+Q^{2}+2PQcos\alpha},\) লব্ধির দিক \(\theta=\tan^{-1}\left(\frac{Qsin\alpha}{P+Qcos\alpha}\right)\)
রাঃ ২০১৬,২০১২,২০০৭; দিঃ ২০১৩; কুঃ২০১১,২০০৯,২০০৭; চঃ ২০১৫,২০১৩,২০০৮; যঃ ২০০৯,২০০৬; বঃ ২০১৫,২০১২; সিঃ২০১১,২০০৭; মাঃ ২০১৫,২০১২,২০১০
উত্তরঃ লব্ধির মান \(R=\sqrt{P^{2}+Q^{2}+2PQcos\alpha},\) লব্ধির দিক \(\theta=\tan^{-1}\left(\frac{Qsin\alpha}{P+Qcos\alpha}\right)\)
রাঃ ২০১৬,২০১২,২০০৭; দিঃ ২০১৩; কুঃ২০১১,২০০৯,২০০৭; চঃ ২০১৫,২০১৩,২০০৮; যঃ ২০০৯,২০০৬; বঃ ২০১৫,২০১২; সিঃ২০১১,২০০৭; মাঃ ২০১৫,২০১২,২০১০
এক বিন্দুতে নির্দিষ্ট কোণে ক্রিয়ারত দুইটি বলের লব্ধির বৃহত্তম ও ক্ষুদ্রতম মান নির্ণয় কর।
উত্তরঃ লব্ধির বৃহত্তম মান \(R_{max}=P+Q,\) লব্ধির ক্ষুদ্রতম মান \(R_{min}=P-Q\)
উত্তরঃ লব্ধির বৃহত্তম মান \(R_{max}=P+Q,\) লব্ধির ক্ষুদ্রতম মান \(R_{min}=P-Q\)
বল সংযোজনের ত্রিভুজ সূত্র
বর্ণনাঃ একই বিন্দুতে ক্রিয়াশীল দুইটি বলের মান ও দিক কোন ত্রিভুজের একইক্রমে গ্রিহীত দুইটি বাহু দ্বারা সূচিত হলে, তাদের লব্ধির মান ও দিক ঐ ত্রিভুজের বিপরীতক্রমে গৃহীত তৃতীয় বাহু দ্বারা সূচিত হবে।
বল সংযোজনের বহুভুজ সূত্র
বর্ণনাঃ একই বিন্দুতে ক্রিয়াশীল \((n-1)\) সংখ্যক বলের মান ও দিক কোন n সংখ্যক বাহুবিশিষ্ট বহুভুজের একইক্রমে গ্রিহীত \((n-1)\) সংখ্যক বাহু দ্বারা সূচিত হলে, তাদের লব্ধির মান ও দিক ঐ বহুভুজের বিপরীতক্রমে গৃহীত \(n\) তম বাহু দ্বারা সূচিত হবে।
প্রমান কর যে, কোন \(O\) বিন্দুতে \(OA\) এবং \(AB\) রেখা বরাবর ক্রিয়াশীল দুইটি বলের মান যথাক্রমে \(m.OA\) এবং \(n.OB\) দ্বারা সূচিত হলে, উক্ত বলদ্বয়ের লব্ধির মান ও দিক \((m+n)OC\) দ্বারা সূচিত হবে, \(C\) বিন্দুটি \(AB\) এর উপর এমনভাবে অবস্থিত হবে যে, \(m.AC=n.BC\) হবে; অর্থাৎ \(C\) বিন্দুটি \(AB\) রেখাকে \(n:m\) অনুপাতে অন্তর্বিভক্ত করবে।
একটি বিশেষ ক্ষেত্র
বর্ণনাঃ \(m=n=1\) হলে, \(\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OC}\).হবে এবং AB রেখার মধ্যবিন্দু C হবে। সুতরাং কোন বিন্দুতে ক্র্রিয়ারত দুইটি বলের মান ও দিক ঐ বিন্দু থেকে অংকিত কোন ত্রিভুজের দুইটি বাহু দ্বারা সূচিত হলে, তাদের লব্ধির মান ও দিক ঐ বিন্দু থেকে অংকিত মধ্যমার দ্বিগুণ দ্বারা সূচিত হবে।
বলের অংশক বা উপাংশ
Component of forces
বলের বিভাজনঃ একটি বলকে দুই বা ততোধিক বলে বিভক্ত করাকে বলের বিভাজন বলে।
উপাংশঃ বিভাজিত বলগুলিকে মূল বলের অংশক বা উপাংশ বলে। আর এ অংশক সমূহের লব্ধি অবশ্যই মূল বল হবে।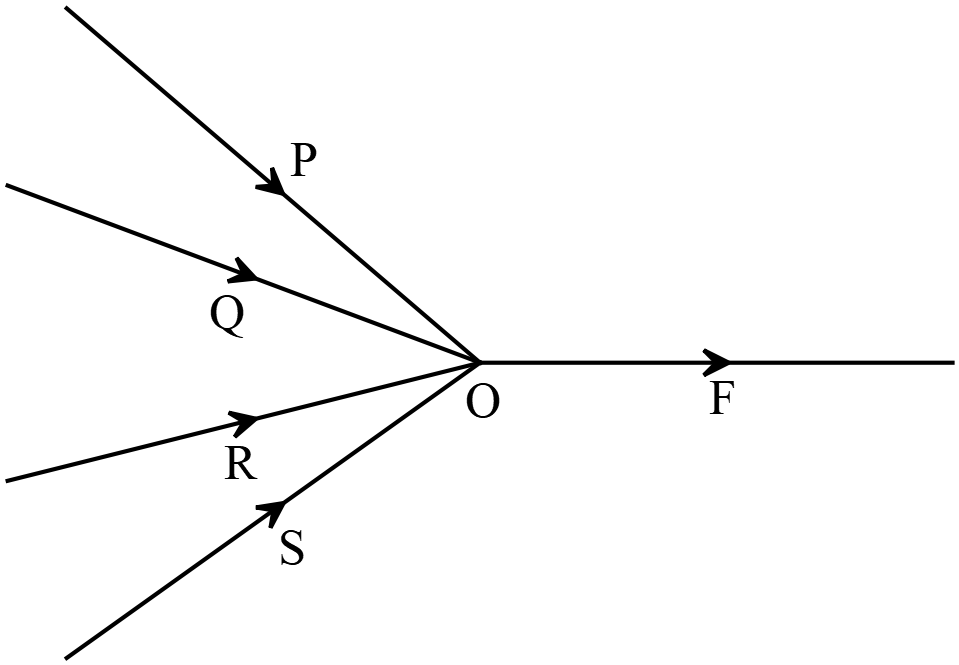
অর্থাৎ কোনো বস্তুকণার উপর একাধিক বল প্রযুক্ত হওয়ার ফলে বস্তুকণাটির উপর যে প্রভাব পড়ে, যদি কোনো একটি বল প্রয়োগের ফলে ঐ বস্তুকণার উপর একই প্রভাব পড়ে, তবে প্রথমোক্ত একাধিক বলগুলির প্রত্যেককে পরের ঐ একটি বলের অংশক বা উপাংশ বলে।
যেমনঃ মনে করি \(P, Q, R\) ও \(S\) এই চারটি বল একটি বস্তুকণা \(O\) তে ক্রিয়া করে এবং বলগুলির সম্মিলিত ক্রিয়াফল অপর একটি বল \(F\) এর ক্রিয়ার সমান হয়। তাহলে \(P, Q, R\) ও \(S\) কে \(F\) বলের অংশক বলা হয়। দ্রষ্টব্যঃ একটি বিন্দুতে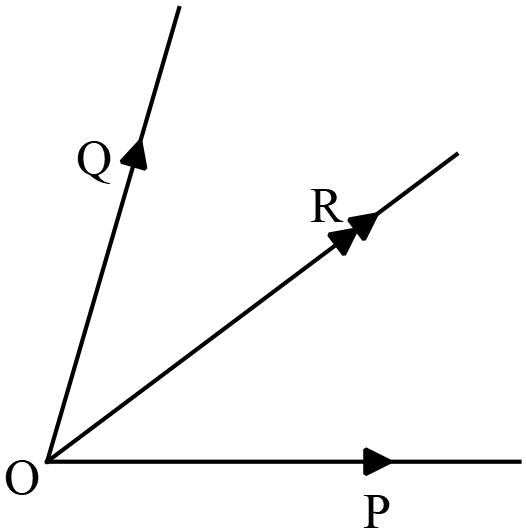
দুইটি বল ক্রিয়াশীল হলে তাদের একটি লব্ধি বল থাকবে। উক্ত বলদ্বয়কে ঐ লব্ধি বলের অংশক বা উপাংশ বলা হয়। অর্থাৎ \(O\) বিন্দুতে \(P\) ও \(Q\) বলদ্বয় ক্রিয়াশীল হলে তাদের লব্ধি \(R\) হয়। তাহলে \(R\) বলের অংশক বা উপাংশ বলদ্বয় \(P\) ও \(Q\) হবে।
উপাংশঃ বিভাজিত বলগুলিকে মূল বলের অংশক বা উপাংশ বলে। আর এ অংশক সমূহের লব্ধি অবশ্যই মূল বল হবে।

অর্থাৎ কোনো বস্তুকণার উপর একাধিক বল প্রযুক্ত হওয়ার ফলে বস্তুকণাটির উপর যে প্রভাব পড়ে, যদি কোনো একটি বল প্রয়োগের ফলে ঐ বস্তুকণার উপর একই প্রভাব পড়ে, তবে প্রথমোক্ত একাধিক বলগুলির প্রত্যেককে পরের ঐ একটি বলের অংশক বা উপাংশ বলে।
যেমনঃ মনে করি \(P, Q, R\) ও \(S\) এই চারটি বল একটি বস্তুকণা \(O\) তে ক্রিয়া করে এবং বলগুলির সম্মিলিত ক্রিয়াফল অপর একটি বল \(F\) এর ক্রিয়ার সমান হয়। তাহলে \(P, Q, R\) ও \(S\) কে \(F\) বলের অংশক বলা হয়। দ্রষ্টব্যঃ একটি বিন্দুতে

দুইটি বল ক্রিয়াশীল হলে তাদের একটি লব্ধি বল থাকবে। উক্ত বলদ্বয়কে ঐ লব্ধি বলের অংশক বা উপাংশ বলা হয়। অর্থাৎ \(O\) বিন্দুতে \(P\) ও \(Q\) বলদ্বয় ক্রিয়াশীল হলে তাদের লব্ধি \(R\) হয়। তাহলে \(R\) বলের অংশক বা উপাংশ বলদ্বয় \(P\) ও \(Q\) হবে।
কোন নির্দিষ্ট দিকে একটি বলের অংশক বা উপাংশ নির্ণয় (বলের সাইন সূত্র )
Determine the component or fraction of a force in a given direction
বলের সাইন সূত্রঃ একটি বল এবং তার অংশকদ্বয় নিয়ে মোট তিনটি বলের প্রত্যেকটির মাণ অপর দুইটির মধ্যবর্তী কোণের সাইনের সমানুপাতিক।
বর্ণনাঃ মনে করি,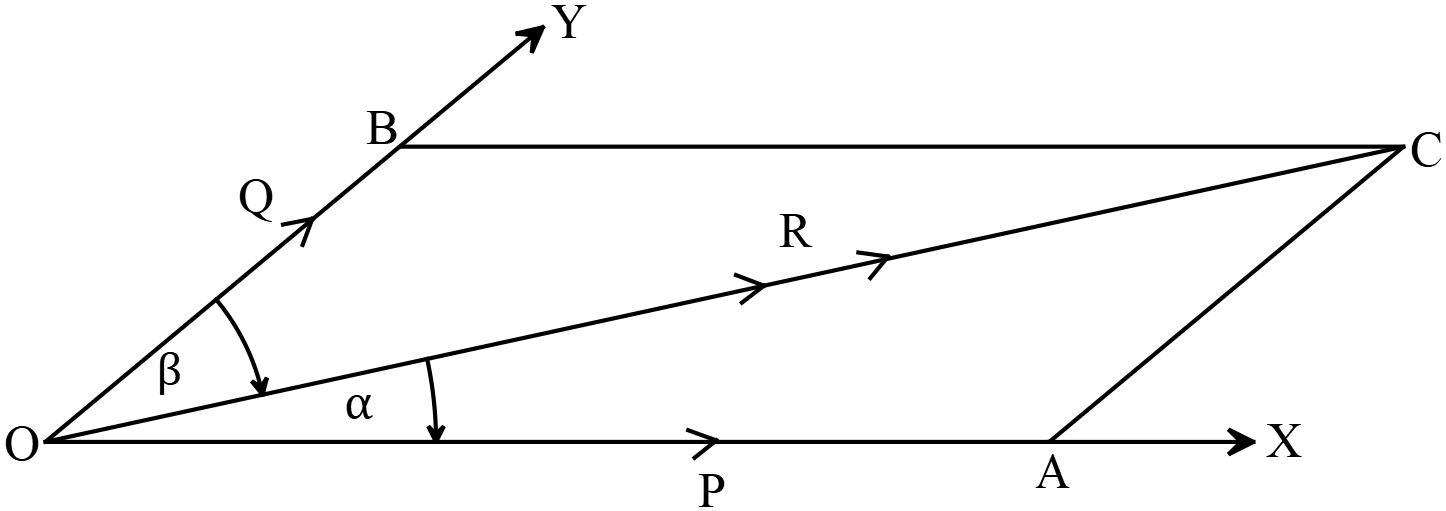
\(OC\) সরলরেখাটি নির্দিষ্ট \(R\) বলের মান ও দিক সূচিত করে এবং \(OX\) ও \(OY\) সরলরেখাদ্বয় \(OC\) রেখার বিপরীত পার্শ্বে তার সাথে যথাক্রমে \(\alpha\) ও \(\beta\) কোণ উৎপন্ন করে। তাহলে \(\angle COX=\alpha\) এবং \(\angle COY=\beta\).
এখন \(C\) থেকে \(OX\) এর উপর \(CA\) এবং \(OY\) এর উপর \(CB\) রেখাংশ অঙ্কন করি যেন \(AC\parallel{OY}\) এবং \(BC\parallel{OX}\) হয়। তাহলে \(OACB\) একটি সামান্তরিক \(OC\) এর একটি কর্ণ।
ধরি, \(OA\) এবং \(OB\) বরাবর \(R\) বলের অংশক বলদ্বয় যথাক্রমে \(P\) ও \(Q\) ।
এখন \(\triangle{OAC}\) হতে সাইন সূত্র প্রয়োগ করে পাই,
\(\frac{OA}{\sin{\angle ACO}}=\frac{AC}{\sin{\angle AOC}}=\frac{OC}{\sin{\angle OAC}}\) ➜ \(\because \frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\)
\(\Rightarrow \frac{OA}{\sin{\beta}}=\frac{OB}{\sin{\alpha}}=\frac{OC}{\sin{\left\{180^{o}-(\alpha+\beta)\right\}}}\)
\(\Rightarrow \frac{P}{\sin{\beta}}=\frac{Q}{\sin{\alpha}}=\frac{R}{\sin{(\alpha+\beta)}}\)
\(\Rightarrow \frac{P}{\sin{\beta}}=\frac{R}{\sin{(\alpha+\beta)}}\), \(\frac{Q}{\sin{\alpha}}=\frac{R}{\sin{(\alpha+\beta)}}\)
\(\Rightarrow P=\frac{R\sin\beta}{\sin(\alpha+\beta)}, Q=\frac{R\sin\alpha}{\sin(\alpha+\beta)}\)
অতএব \(R\) বলের বিভাজিত অংশকদ্বয় যথাক্রমে, \(P=\frac{R\sin{\beta}}{\sin{(\alpha+\beta)}}\), \(Q=\frac{R\sin{\alpha}}{\sin{(\alpha+\beta)}}\)
অতএব, বলের অংশকদ্বয় ও তাদের লব্ধি বলের প্রত্যেককেই একটি অপর দুইটির মধ্যবর্তী কোণের সাইনের সমানুপাতিক। এটিকে বলের সাইন সূত্র বলা হয়। যা শুধুমাত্র একটি বল এবং তার উপাংশদ্বয়ের মধ্যে সম্পর্ক বুঝায়।
বর্ণনাঃ মনে করি,

\(OC\) সরলরেখাটি নির্দিষ্ট \(R\) বলের মান ও দিক সূচিত করে এবং \(OX\) ও \(OY\) সরলরেখাদ্বয় \(OC\) রেখার বিপরীত পার্শ্বে তার সাথে যথাক্রমে \(\alpha\) ও \(\beta\) কোণ উৎপন্ন করে। তাহলে \(\angle COX=\alpha\) এবং \(\angle COY=\beta\).
এখন \(C\) থেকে \(OX\) এর উপর \(CA\) এবং \(OY\) এর উপর \(CB\) রেখাংশ অঙ্কন করি যেন \(AC\parallel{OY}\) এবং \(BC\parallel{OX}\) হয়। তাহলে \(OACB\) একটি সামান্তরিক \(OC\) এর একটি কর্ণ।
ধরি, \(OA\) এবং \(OB\) বরাবর \(R\) বলের অংশক বলদ্বয় যথাক্রমে \(P\) ও \(Q\) ।
এখন \(\triangle{OAC}\) হতে সাইন সূত্র প্রয়োগ করে পাই,
\(\frac{OA}{\sin{\angle ACO}}=\frac{AC}{\sin{\angle AOC}}=\frac{OC}{\sin{\angle OAC}}\) ➜ \(\because \frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\)
\(\Rightarrow \frac{OA}{\sin{\beta}}=\frac{OB}{\sin{\alpha}}=\frac{OC}{\sin{\left\{180^{o}-(\alpha+\beta)\right\}}}\)
\(\Rightarrow \frac{P}{\sin{\beta}}=\frac{Q}{\sin{\alpha}}=\frac{R}{\sin{(\alpha+\beta)}}\)
\(\Rightarrow \frac{P}{\sin{\beta}}=\frac{R}{\sin{(\alpha+\beta)}}\), \(\frac{Q}{\sin{\alpha}}=\frac{R}{\sin{(\alpha+\beta)}}\)
\(\Rightarrow P=\frac{R\sin\beta}{\sin(\alpha+\beta)}, Q=\frac{R\sin\alpha}{\sin(\alpha+\beta)}\)
অতএব \(R\) বলের বিভাজিত অংশকদ্বয় যথাক্রমে, \(P=\frac{R\sin{\beta}}{\sin{(\alpha+\beta)}}\), \(Q=\frac{R\sin{\alpha}}{\sin{(\alpha+\beta)}}\)
অতএব, বলের অংশকদ্বয় ও তাদের লব্ধি বলের প্রত্যেককেই একটি অপর দুইটির মধ্যবর্তী কোণের সাইনের সমানুপাতিক। এটিকে বলের সাইন সূত্র বলা হয়। যা শুধুমাত্র একটি বল এবং তার উপাংশদ্বয়ের মধ্যে সম্পর্ক বুঝায়।
বলের লম্বাংশ
Resolved parts of forces
লম্বাংশঃ যদি একটি বলের দুইটি উপাংশ থাকে এবং উক্ত উপাংশ বলদ্বয় পরস্পর লম্বভাবে অর্থাৎ \(90^{o}\) কোণে ক্রিয়াশীল হয়, তবে উক্ত উপাংশ বলদ্বয়কে ঐ বলটির লম্বাংশ বলে।
বলের লম্বাংশ নির্ণয়ঃ মনে করি,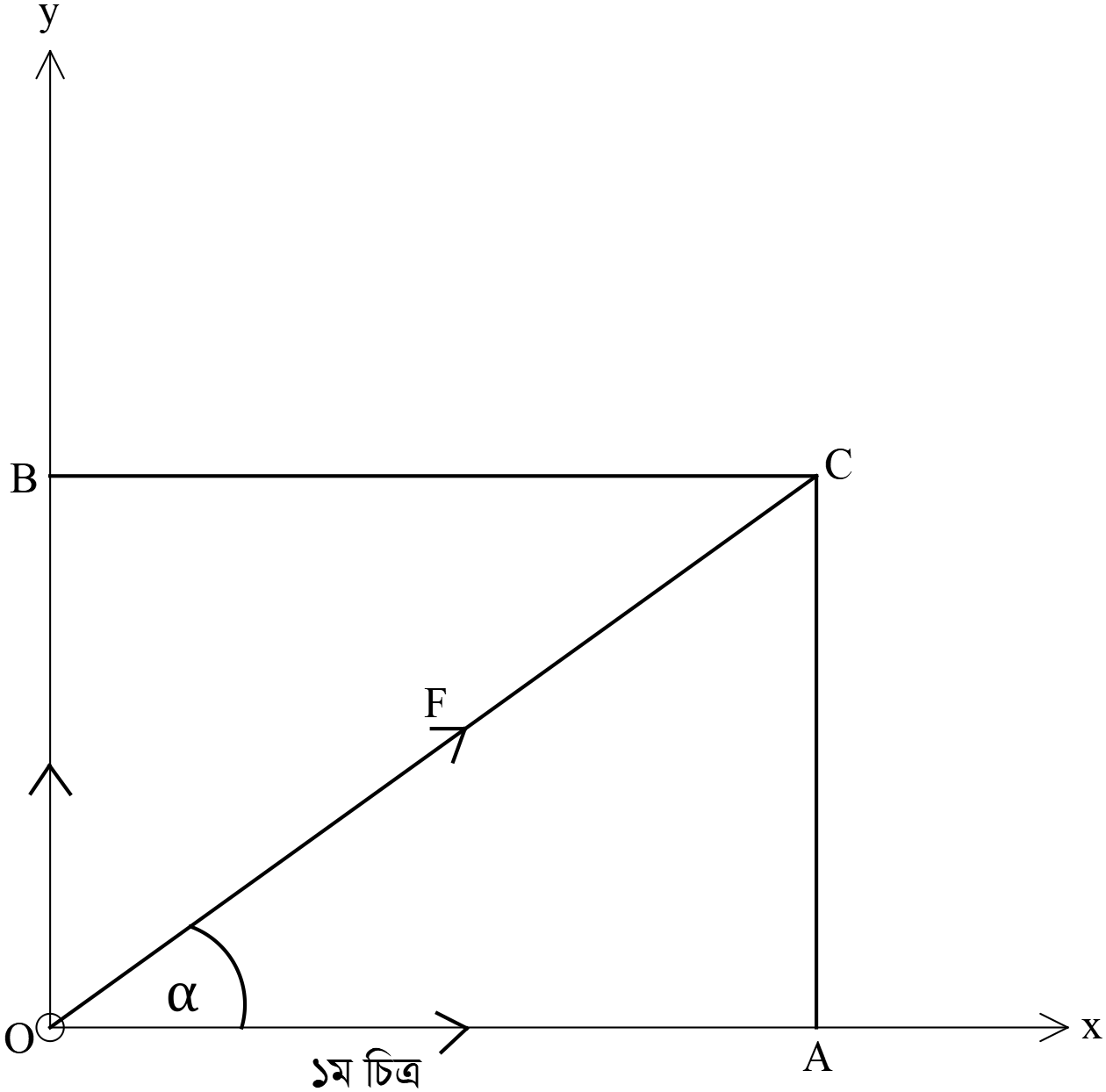
\(OX\) ও \(OY\) পরস্পর দুইটি লম্ব সরলরেখা \(OX\) এর সাথে \(\alpha\) কোণে আনত একটি সরলরেখা \(OC\) যা একটি নির্দিষ্ট বল \(F\) কে সূচিত করে। \(C\) বিন্দু থেকে \(OX\) ( বা \(OX^{\prime}\)) এর উপর \(CA\) এবং \(OY\) এর উপর \(CB\) লম্ব অঙ্কন করি। তাহলে \(OACB\) একটি আয়তক্ষেত্র উৎপন্ন হয়। \(OC\) এর একটি কর্ণ। সুতরাং বলের সামান্তরিক সূত্রানুসারে \(F\) বলের লম্বাংশদ্বয় যথাক্রমে \(OA\) এবং \(OB\) দ্বারা সূচিত হবে।
১ম চিত্র হতে, \(\cos{\angle{COA}}=\frac{OA}{OC}\) \(\Rightarrow \cos{\alpha}=\frac{OA}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F \)
\(\therefore OA=F\cos{\alpha}\) আবার, \(\sin{\angle{COA}}=\frac{AC}{OC}\) \(\Rightarrow \sin{\alpha}=\frac{OB}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F, AC=OB\)
\(\therefore OB=F\sin{\alpha}\)
সুতরাং \(X\) অক্ষের সাথে \(\alpha\) কোণে আনত বলের লম্বাংশদ্বয় যথাক্রমে \(F\cos{\alpha}\) ও \(F\sin{\alpha}\)।
২য় চিত্র হতে,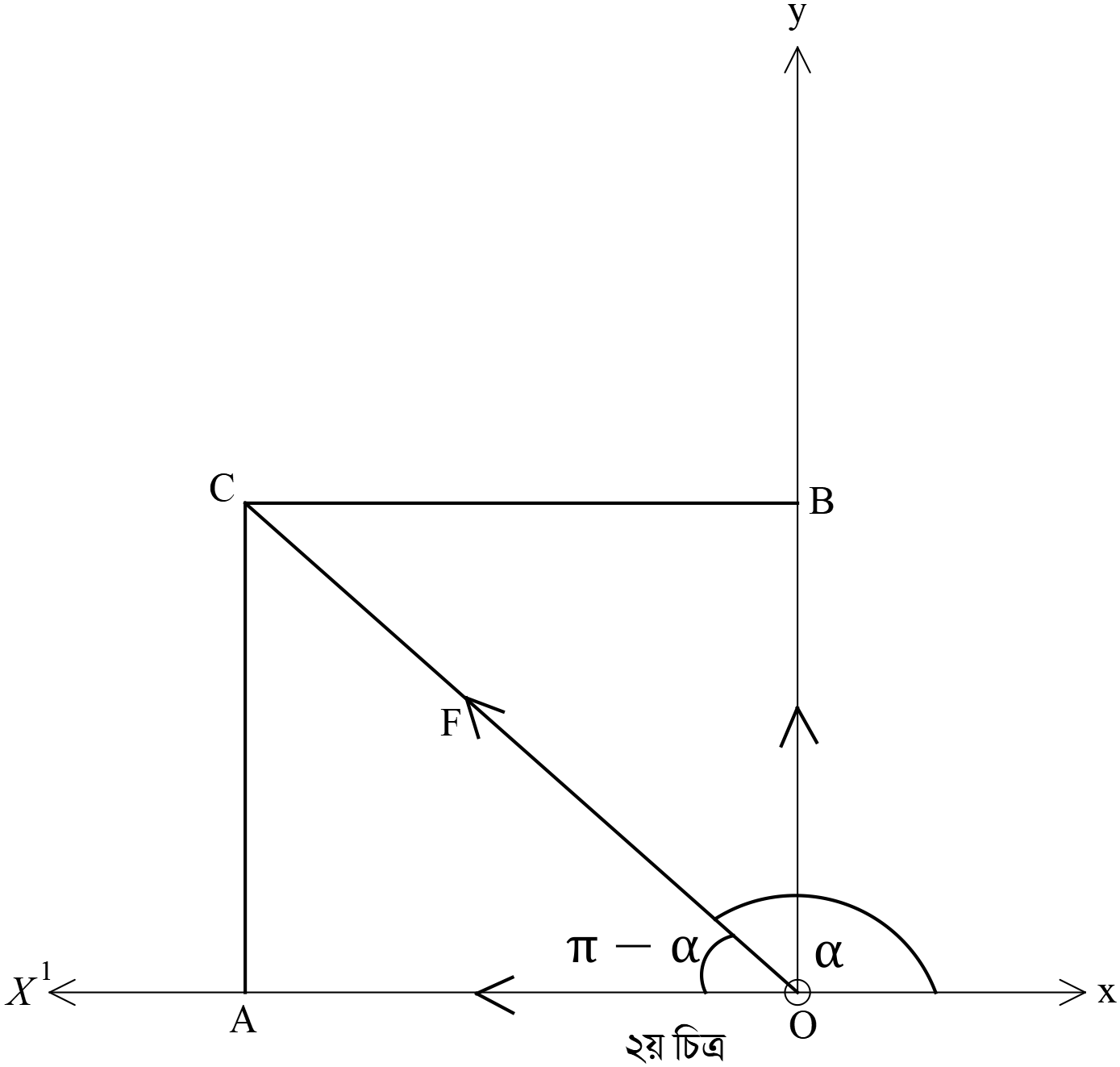
\(\angle{COA}=\pi-\alpha\) \(\cos{\angle{COA}}=\frac{OA}{OC}\) \(\Rightarrow \cos{(\pi-\alpha)}=\frac{OA}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F \)
\(\Rightarrow -\cos{\alpha}=\frac{OA}{F}\)
\(\therefore OA=-F\cos{\alpha}\)
আবার,
\(\sin{\angle{COA}}=\frac{AC}{OC}\)
\(\Rightarrow \sin{(\pi-\alpha)}=\frac{OB}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F, AC=OB\)
\(\Rightarrow \sin{\alpha}=\frac{OB}{F}\)
\(\therefore OB=F\sin{\alpha}\)
সুতরাং \(X^{\prime}\) অক্ষের সাথে \(\alpha\) কোণে আনত বলের লম্বাংশদ্বয় যথাক্রমে \(-F\cos{\alpha}\) ও \(F\sin{\alpha}\)।
\(\therefore \) অনুভূমিক \(OX\) বরাবর \(F\) এর লম্বাংশ \(=-OA=-(-F\cos{\alpha})=F\cos{\alpha}\)
এবং লম্বিক \(OY\) বরাবর \(F\) এর লম্বাংশ \(=F\sin{\alpha}\)
দ্রষ্টব্যঃ নির্দিষ্ট দিকে কোনো বলের লম্বাংশ = বল \(\times\) ( বল ও নির্দিষ্ট দিকের অন্তর্গত কোণের সাইন )
সুতরাং কোন নির্দিষ্ট দিকে কোন বলের লম্বাংশ ঐ বল ও তার সাথে নির্দিষ্ট দিকে যে কোণ উৎপন্ন করে তার Cosine এর গুণফলের সমান।
দ্রষ্টব্যঃ \(\overrightarrow{OA}=F\cos{\alpha}\)
\(\Rightarrow F\cos{\alpha}=\overrightarrow{OA}\)
\(\Rightarrow F\times\frac{|\overrightarrow{OA}|}{|\overrightarrow{OC}|}=\overrightarrow{OA}\)
\(\Rightarrow F=\frac{|\overrightarrow{OC}|}{|\overrightarrow{OA}|}\times\overrightarrow{OA}\)
\(\therefore \overrightarrow{OC}=\frac{|\overrightarrow{OC}|}{|\overrightarrow{OA}|}\times\overrightarrow{OA}\)
বলের লম্বাংশ নির্ণয়ঃ মনে করি,

\(OX\) ও \(OY\) পরস্পর দুইটি লম্ব সরলরেখা \(OX\) এর সাথে \(\alpha\) কোণে আনত একটি সরলরেখা \(OC\) যা একটি নির্দিষ্ট বল \(F\) কে সূচিত করে। \(C\) বিন্দু থেকে \(OX\) ( বা \(OX^{\prime}\)) এর উপর \(CA\) এবং \(OY\) এর উপর \(CB\) লম্ব অঙ্কন করি। তাহলে \(OACB\) একটি আয়তক্ষেত্র উৎপন্ন হয়। \(OC\) এর একটি কর্ণ। সুতরাং বলের সামান্তরিক সূত্রানুসারে \(F\) বলের লম্বাংশদ্বয় যথাক্রমে \(OA\) এবং \(OB\) দ্বারা সূচিত হবে।
১ম চিত্র হতে, \(\cos{\angle{COA}}=\frac{OA}{OC}\) \(\Rightarrow \cos{\alpha}=\frac{OA}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F \)
\(\therefore OA=F\cos{\alpha}\) আবার, \(\sin{\angle{COA}}=\frac{AC}{OC}\) \(\Rightarrow \sin{\alpha}=\frac{OB}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F, AC=OB\)
\(\therefore OB=F\sin{\alpha}\)
সুতরাং \(X\) অক্ষের সাথে \(\alpha\) কোণে আনত বলের লম্বাংশদ্বয় যথাক্রমে \(F\cos{\alpha}\) ও \(F\sin{\alpha}\)।
২য় চিত্র হতে,

\(\angle{COA}=\pi-\alpha\) \(\cos{\angle{COA}}=\frac{OA}{OC}\) \(\Rightarrow \cos{(\pi-\alpha)}=\frac{OA}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F \)
\(\Rightarrow -\cos{\alpha}=\frac{OA}{F}\)
\(\therefore OA=-F\cos{\alpha}\)
আবার,
\(\sin{\angle{COA}}=\frac{AC}{OC}\)
\(\Rightarrow \sin{(\pi-\alpha)}=\frac{OB}{F}\) ➜ \(\because \angle{COA}=\alpha, OC=F, AC=OB\)
\(\Rightarrow \sin{\alpha}=\frac{OB}{F}\)
\(\therefore OB=F\sin{\alpha}\)
সুতরাং \(X^{\prime}\) অক্ষের সাথে \(\alpha\) কোণে আনত বলের লম্বাংশদ্বয় যথাক্রমে \(-F\cos{\alpha}\) ও \(F\sin{\alpha}\)।
\(\therefore \) অনুভূমিক \(OX\) বরাবর \(F\) এর লম্বাংশ \(=-OA=-(-F\cos{\alpha})=F\cos{\alpha}\)
এবং লম্বিক \(OY\) বরাবর \(F\) এর লম্বাংশ \(=F\sin{\alpha}\)
দ্রষ্টব্যঃ নির্দিষ্ট দিকে কোনো বলের লম্বাংশ = বল \(\times\) ( বল ও নির্দিষ্ট দিকের অন্তর্গত কোণের সাইন )
সুতরাং কোন নির্দিষ্ট দিকে কোন বলের লম্বাংশ ঐ বল ও তার সাথে নির্দিষ্ট দিকে যে কোণ উৎপন্ন করে তার Cosine এর গুণফলের সমান।
দ্রষ্টব্যঃ \(\overrightarrow{OA}=F\cos{\alpha}\)
\(\Rightarrow F\cos{\alpha}=\overrightarrow{OA}\)
\(\Rightarrow F\times\frac{|\overrightarrow{OA}|}{|\overrightarrow{OC}|}=\overrightarrow{OA}\)
\(\Rightarrow F=\frac{|\overrightarrow{OC}|}{|\overrightarrow{OA}|}\times\overrightarrow{OA}\)
\(\therefore \overrightarrow{OC}=\frac{|\overrightarrow{OC}|}{|\overrightarrow{OA}|}\times\overrightarrow{OA}\)
লম্বাংশের উপপাদ্য
Prolongation Theorem
বর্ণনাঃ কোন বিন্দুতে ক্রিয়ারত দুইটি বলের কোন নির্দিষ্ট দিকের লম্বাংশের বীজগাণিতিক যোগফল তাদের লব্ধির উক্ত দিকের লম্বাংশের সমান।
লম্বাংশের সাহায্যে দুইটি বলের লব্ধির মাণ ও দিক নির্ণয়
Determine the magnitude and direction of acceleration of two Forces with the help of Prolongation Theorem
মনে করি, বলগুলোর লব্ধি \(O\) বিন্দুতে পরস্পর \(\alpha\) কোণে একই সময়ে ক্রিয়ারত \(P\) ও \(Q\) দুইটি বল যথাক্রমে \(OA\) ও \(OB\) দ্বারা মাণে ও দিকে সূচিত হয়। ধরি, \(OC\) দ্বারা মাণে ও দিকে সূচিত বলদ্বয়ের লব্ধি \(R,\) যা \(OA\) এর সাথে \(\theta\) কোণ উৎপন্ন করে।
\(OA\) বরাবর লম্বাংশ নিয়ে পাই, 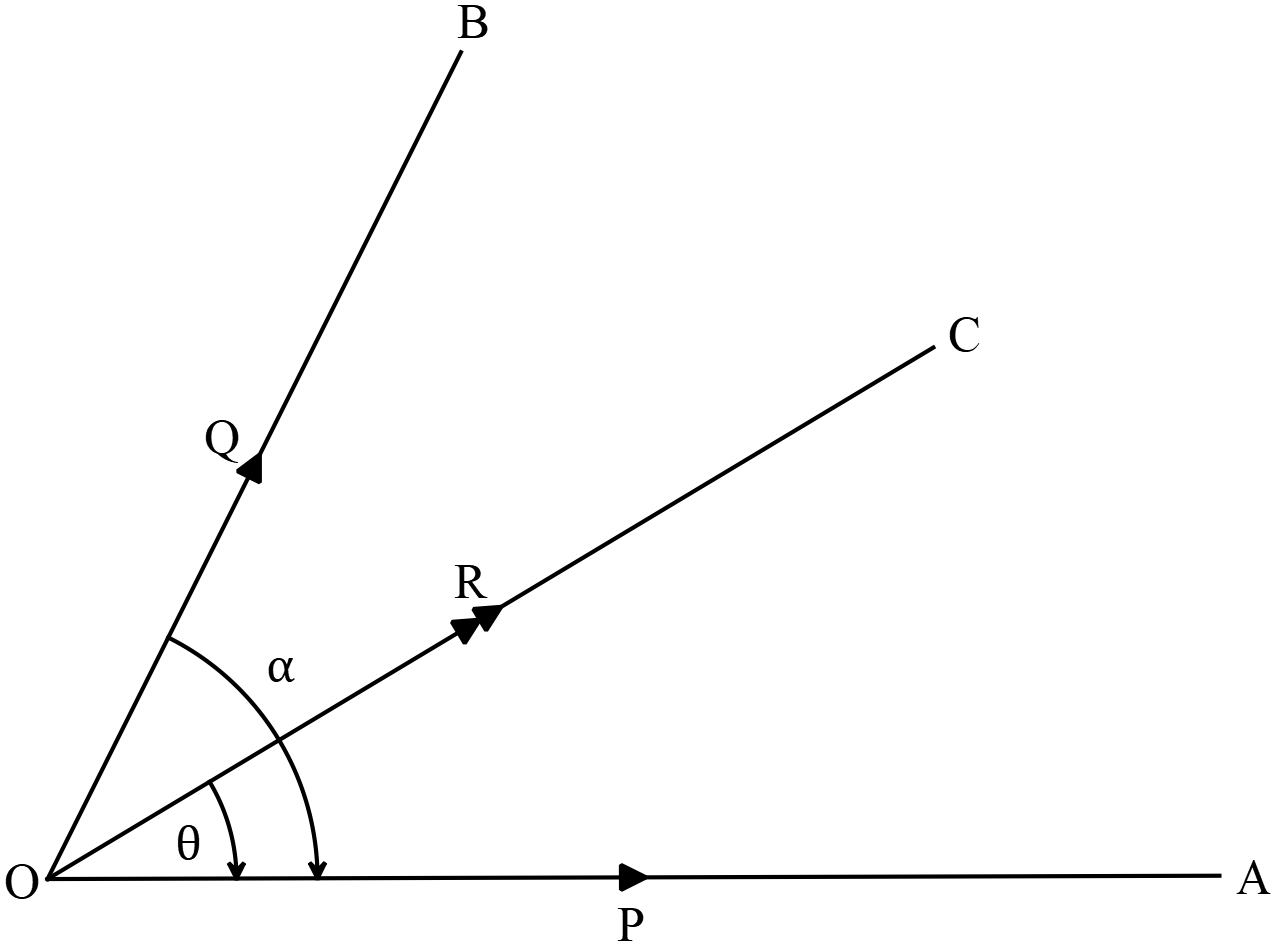
\(R\cos{\theta}=P\cos{0^{o}}+Q\cos{\alpha} \) ➜ লম্বাংশের উপপাদ্য অনুসারে।
\(\Rightarrow R\cos{\theta}=P.1+Q\cos{\alpha}\) ➜ \(\because \cos{0^{o}}=1\)
\(\therefore R\cos{\theta}=P+Q\cos{\alpha}.......(1) \)
এবং \(OA\) এর উপর লম্ব বরাবর লম্বাংশ নিয়ে পাই,
\(R\sin{\theta}=P\sin{0^{o}}+Q\sin{\alpha}\)
\(\Rightarrow R\sin{\theta}=P.0+Q\sin{\alpha}\) ➜ \(\because \sin{0^{o}}=0\)
\(\Rightarrow R\sin{\theta}=0+Q\sin{\alpha} \)
\(\therefore R\sin{\theta}=Q\sin{\alpha}.....(2) \)
\((1)\) ও \((2)\) বর্গকরে যোগ করি,
\(R^{2}\cos^{2}{\theta}+R^{2}\sin^{2}{\theta}=(P+Q\cos{\alpha})^{2}+(Q\sin{\alpha})^{2}\)
\(\Rightarrow R^{2}(\sin^{2}{\theta}+\cos^{2}{\theta})=P^{2}+2PQ\cos{\alpha}+Q^2\cos^2{\alpha}+Q^2\sin^2{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^2(\cos^2{\alpha}+\sin^2{\alpha})\) ➜ \(\because \sin^{2}{A}+\cos^{2}{A}=1\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^2\) ➜ \(\because \sin^{2}{A}+\cos^{2}{A}=1\)
\(\Rightarrow R^{2}=P^{2}+Q^2+2PQ\cos{\alpha}\)
\(\therefore R=\sqrt{P^{2}+Q^2+2PQ\cos{\alpha}}\)
আবার,
\((2)\) কে \((1)\) দ্বারা ভাগ করি,
\(\frac{R\sin{\theta}}{R\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
\(R\) ও \(\theta\) এর মান থেকে লব্ধির মান ও দিক পাওয়া যাবে।

\(R\cos{\theta}=P\cos{0^{o}}+Q\cos{\alpha} \) ➜ লম্বাংশের উপপাদ্য অনুসারে।
\(\Rightarrow R\cos{\theta}=P.1+Q\cos{\alpha}\) ➜ \(\because \cos{0^{o}}=1\)
\(\therefore R\cos{\theta}=P+Q\cos{\alpha}.......(1) \)
এবং \(OA\) এর উপর লম্ব বরাবর লম্বাংশ নিয়ে পাই,
\(R\sin{\theta}=P\sin{0^{o}}+Q\sin{\alpha}\)
\(\Rightarrow R\sin{\theta}=P.0+Q\sin{\alpha}\) ➜ \(\because \sin{0^{o}}=0\)
\(\Rightarrow R\sin{\theta}=0+Q\sin{\alpha} \)
\(\therefore R\sin{\theta}=Q\sin{\alpha}.....(2) \)
\((1)\) ও \((2)\) বর্গকরে যোগ করি,
\(R^{2}\cos^{2}{\theta}+R^{2}\sin^{2}{\theta}=(P+Q\cos{\alpha})^{2}+(Q\sin{\alpha})^{2}\)
\(\Rightarrow R^{2}(\sin^{2}{\theta}+\cos^{2}{\theta})=P^{2}+2PQ\cos{\alpha}+Q^2\cos^2{\alpha}+Q^2\sin^2{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^2(\cos^2{\alpha}+\sin^2{\alpha})\) ➜ \(\because \sin^{2}{A}+\cos^{2}{A}=1\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^2\) ➜ \(\because \sin^{2}{A}+\cos^{2}{A}=1\)
\(\Rightarrow R^{2}=P^{2}+Q^2+2PQ\cos{\alpha}\)
\(\therefore R=\sqrt{P^{2}+Q^2+2PQ\cos{\alpha}}\)
আবার,
\((2)\) কে \((1)\) দ্বারা ভাগ করি,
\(\frac{R\sin{\theta}}{R\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
\(R\) ও \(\theta\) এর মান থেকে লব্ধির মান ও দিক পাওয়া যাবে।
সমবিন্দুগামী যে কোন সংখ্যক একতলীয় বলের লব্ধি নির্ণয়
Determine the Resultant of any number of concentric Forces
নির্দিষ্ট \(O\) বিন্দুর মধ্যদিয়ে একটি নির্দিষ্ট সরলরেখা \(OX\) আঁকি। \(OX\) এর সাথে সমকোণ উৎপন্ন করে এমন একটি রেখা \(OY\) আঁকি।
মনে করি, \(P_{1}, P_{2}, P_{3}, P_{4} .............\) সমবিন্দু বলগুলি \(OX\) এর সাথে যথাক্রমে \(\alpha_{1},\alpha_{2}, \alpha_{3}, \alpha_{4} .............\)কোণ উৎপন্ন করে।
মনে করি, বলগুলোর লব্ধি \(F\) এবং তা \(OX\) এর সাথে \(\theta\) কোণ উপন্ন করে। তাহলে, যেহেতু একই বিন্দুতে ক্রিয়ারত যে কোন সংখ্যক একতলীয় বলের কোন নির্দিষ্ট দিকের লম্বাংশগুলোর বীজগাণিতিক যোগফল তাদের লব্ধির উক্ত দিকের লম্বাংশের সমান। অতএব পৃথকভাবে \(OX\) ও \(OY\) বরাবর বিভাজন করে,
\(F\cos{\theta}=P_{1}\cos{\alpha_{1}}+P_{2}\cos{\alpha_{2}}+P_{3}\cos{\alpha_{3}}....\)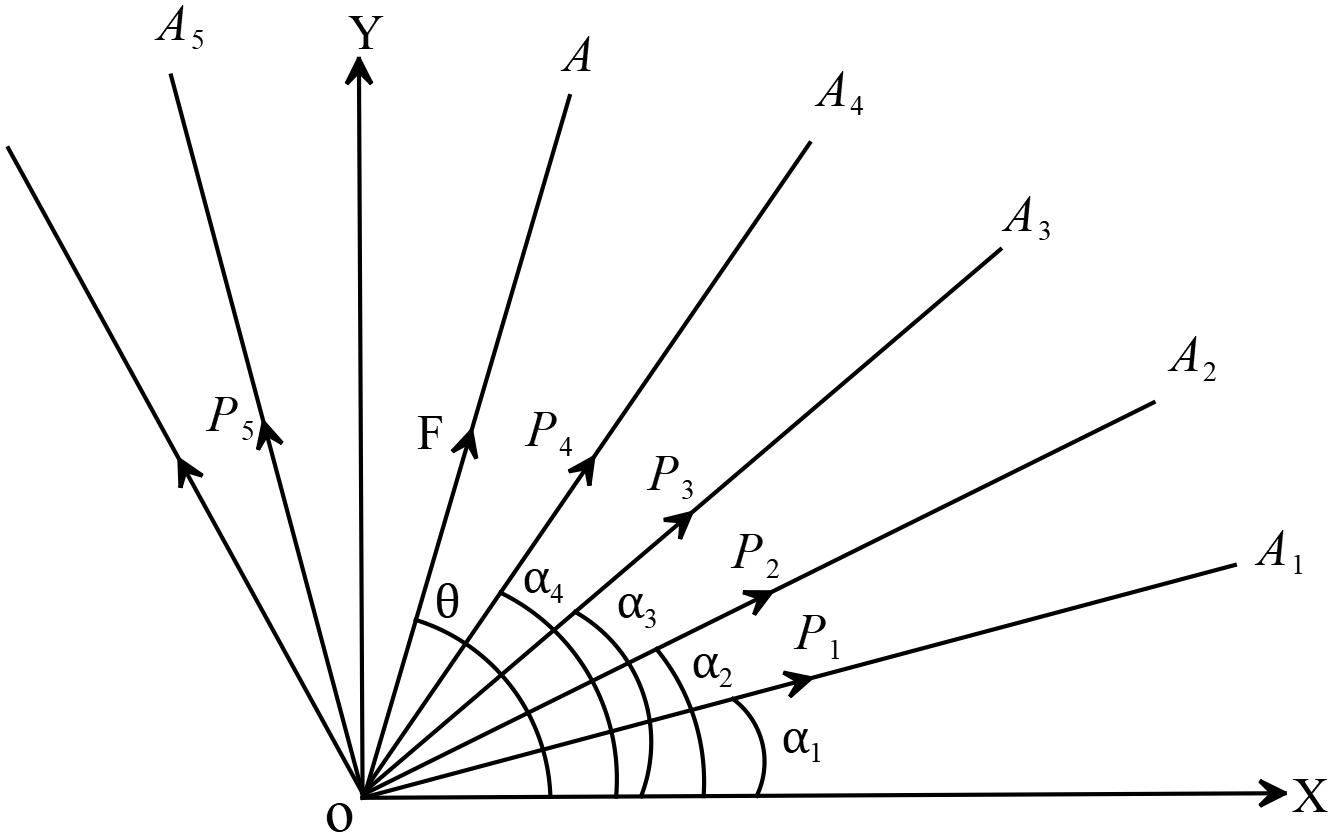
\(\therefore F\cos{\theta}=X....(i)\) ➜ যেখানে, \(X=P_{1}\cos{\alpha_{1}}+P_{2}\cos{\alpha_{2}}+P_{3}\cos{\alpha_{3}}....\)
এবং \(F\sin{\theta}=P_{1}\sin{\alpha_{1}}+P_{2}\sin{\alpha_{2}}+P_{3}\sin{\alpha_{3}}....\)
\(\therefore F\sin{\theta}=Y....(ii)\) ➜ যেখানে, \(Y=P_{1}\sin{\alpha_{1}}+P_{2}\sin{\alpha_{2}}+P_{3}\sin{\alpha_{3}}....\)
\((i)\) ও \((ii)\) বর্গকরে যোগ করি,
\(F^{2}\sin^{2}{\theta}+F^{2}\cos^{2}{\theta}=X^{2}+Y^{2}\)
\(\Rightarrow F^{2}(\sin^{2}{\theta}+\cos^{2}{\theta})=X^{2}+Y^{2}\)
\(\Rightarrow F^{2}=X^{2}+Y^{2}\)
\(\therefore F=\sqrt{X^{2}+Y^{2}}\)
আবার,
\((ii)\) কে \((i)\) দ্বারা ভাগ করি,
\(\frac{F\sin{\theta}}{F\cos{\theta}}=\frac{Y}{X}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Y}{X}\)
\(\Rightarrow \tan{\theta}=\frac{Y}{X}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Y}{X}\right)\)
\(F\) ও \(\theta\) এর মান থেকে লব্ধির মান ও দিক পাওয়া যাবে।
\(F\cos{\theta}=P_{1}\cos{\alpha_{1}}+P_{2}\cos{\alpha_{2}}+P_{3}\cos{\alpha_{3}}....\)

\(\therefore F\cos{\theta}=X....(i)\) ➜ যেখানে, \(X=P_{1}\cos{\alpha_{1}}+P_{2}\cos{\alpha_{2}}+P_{3}\cos{\alpha_{3}}....\)
এবং \(F\sin{\theta}=P_{1}\sin{\alpha_{1}}+P_{2}\sin{\alpha_{2}}+P_{3}\sin{\alpha_{3}}....\)
\(\therefore F\sin{\theta}=Y....(ii)\) ➜ যেখানে, \(Y=P_{1}\sin{\alpha_{1}}+P_{2}\sin{\alpha_{2}}+P_{3}\sin{\alpha_{3}}....\)
\((i)\) ও \((ii)\) বর্গকরে যোগ করি,
\(F^{2}\sin^{2}{\theta}+F^{2}\cos^{2}{\theta}=X^{2}+Y^{2}\)
\(\Rightarrow F^{2}(\sin^{2}{\theta}+\cos^{2}{\theta})=X^{2}+Y^{2}\)
\(\Rightarrow F^{2}=X^{2}+Y^{2}\)
\(\therefore F=\sqrt{X^{2}+Y^{2}}\)
আবার,
\((ii)\) কে \((i)\) দ্বারা ভাগ করি,
\(\frac{F\sin{\theta}}{F\cos{\theta}}=\frac{Y}{X}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Y}{X}\)
\(\Rightarrow \tan{\theta}=\frac{Y}{X}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Y}{X}\right)\)
\(F\) ও \(\theta\) এর মান থেকে লব্ধির মান ও দিক পাওয়া যাবে।
×
বল সামান্তরিক সুত্রটি লিখ এবং এক বিন্দুতে পরস্পর \(\alpha\) কোণে ক্রিয়ারত দুইটি বলের লব্ধির মান ও দিক নির্ণয় কর।
উত্তরঃ লব্ধির মান \(R=\sqrt{P^{2}+Q^{2}+2PQcos\alpha}\) লব্ধির দিক \(\theta=\tan^{-1}(\frac{Qsin\alpha}{P+Qcos\alpha})\)
রাঃ ২০১৬,২০১২,২০০৭;দিঃ ২০১৩;কুঃ২০১১,২০০৯,২০০৭; চঃ ২০১৫,২০১৩,২০০৮;যঃ ২০০৯,২০০৬; বঃ ২০১৫,২০১২; সিঃ২০১১,২০০৭; মাঃ ২০১৫,২০১২,২০১০
উত্তরঃ লব্ধির মান \(R=\sqrt{P^{2}+Q^{2}+2PQcos\alpha}\) লব্ধির দিক \(\theta=\tan^{-1}(\frac{Qsin\alpha}{P+Qcos\alpha})\)
রাঃ ২০১৬,২০১২,২০০৭;দিঃ ২০১৩;কুঃ২০১১,২০০৯,২০০৭; চঃ ২০১৫,২০১৩,২০০৮;যঃ ২০০৯,২০০৬; বঃ ২০১৫,২০১২; সিঃ২০১১,২০০৭; মাঃ ২০১৫,২০১২,২০১০
সমাধানঃ
বলের সামান্তরিক সুত্রঃ যদি কোন সামান্তরিকের দুইটি সন্নিহিত বাহু দ্বারা কোন বিন্দুতে একই সময়ে ক্রিয়ারত দুইটি বলের মান ও দিক সূচিত করা যায়, তাহলে সামান্তরিকের উক্ত বাহুদ্বয়ের ছেদবিন্দুগামী কর্ণ দ্বারা উক্ত বলদ্বয়ের লব্ধির মান ও দিক সূচিত হয়।
লব্ধির মান ও দিক নির্ণয়ঃ মনে করি \(O\) বিন্দতে \(α\) কোণে ক্রিয়াশীল দুইটি বল \(P\) ও \(Q\) এর মান ও দিক যথাক্রমে \(OA\) এবং \(OB\) বাহু দ্বারা সূচিত হয়েছে। \(OACB\) সামান্তরিকটি অংকন করি। তাহলে বলের সামান্তরিক সুত্রানুসারে \(OC\) কর্ণটি ঐ বলদ্বয়ের লব্ধি \(R\) বলের মান ও দিক সূচিত করবে।
\((i)\) নং চিত্রে, \(OA\) এর বর্ধিতাংশের উপর \(CD\) লম্ব অংকন করি।
এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে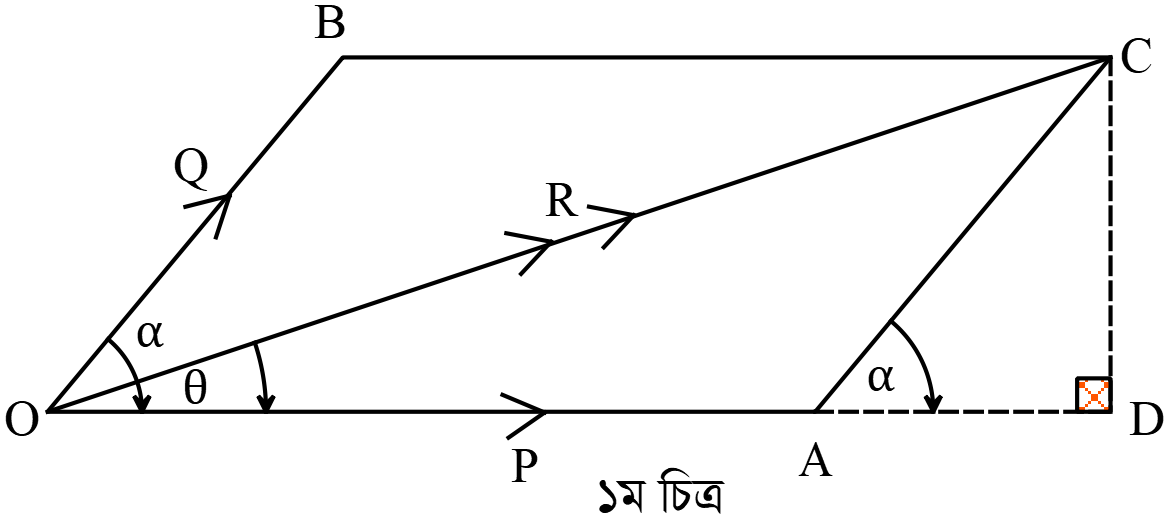
\(OC^{2}=OD^{2}+CD^{2}\Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
\(R\) যদি \(P\) এর দিকের সহিত \(θ\) কোণ উৎপন্ন করে অর্থাৎ \(\angle COD=\theta\) হলে,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA+AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA+AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\) \((ii)\) নং চিত্রে, \(OA\) এর উপর \(CD\) লম্ব অংকন করি।
এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে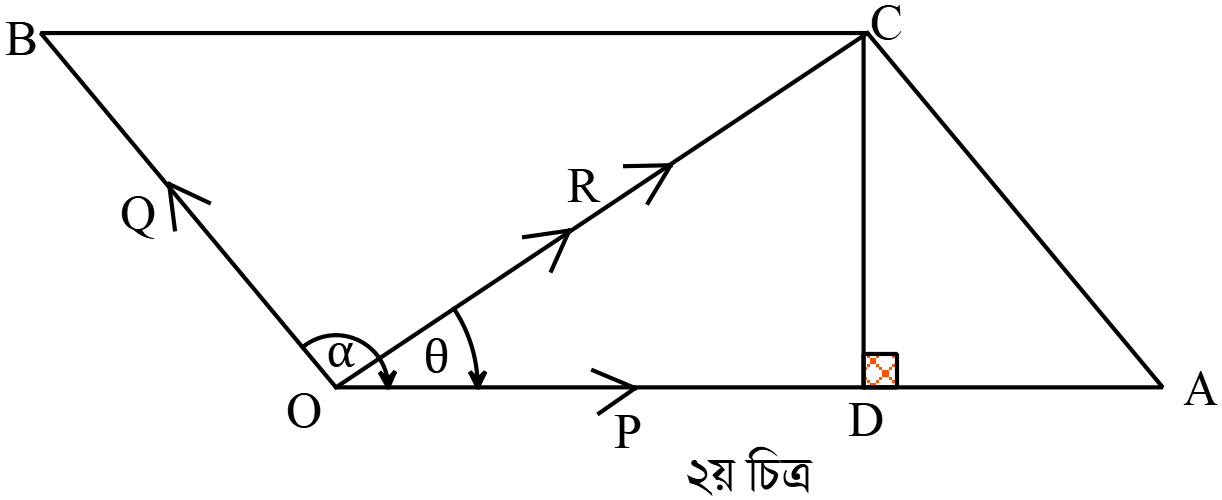
\(OC^{2}=OD^{2}+CD^{2}\Rightarrow OC^{2}=\left\{OA-AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA-AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(\Rightarrow OC^{2}=\left\{OA-AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P-Q\cos{(180^{o}-\alpha)}\right\}^{2}+\left\{Q\sin{(180^{o}-\alpha)}\right\}^{2}\)
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
আবার,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA-AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA-AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{(180^{o}-\alpha)}}{P+Q\cos{(180^{o}-\alpha)}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
অতএব লব্ধির মান ও দিক যথাক্রমে \(R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\) ও \(\theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
আবার,
যদি বল \(Q\) এর সাথে লব্ধি \(\beta\) কোন উৎপন্ন করে সেই ক্ষেত্রে লদ্ধির দিক হবে নিম্নুরুপ
\(\beta=\tan^{-1}\left(\frac{P\sin{\alpha}}{Q+P\cos{\alpha}}\right)\)
এখন \((i)\) নং চিত্রে,\(AD=AC\frac{AD}{AC}=AC.\cos{\angle CAD}=Q\cos{\alpha}\) এবং \(CD=AC\frac{CD}{AC}=AC.\cos{\angle CAD}=Q\sin{\alpha}\)
\(\therefore OD=OA+AD=P+Q\cos{\alpha}\)
\((ii)\) নং চিত্রে,\(AD=AC\frac{AD}{AC}=AC.\cos{\angle CAD}=Q\cos{(180^{o}-\alpha)}=-Q\cos{\alpha}\)
\(\therefore OD=OA-AD=P+Q\cos{\alpha}\)
এবং \(CD=AC\frac{CD}{AC}=AC.\sin{\angle CAD}=Q\sin{(180^{o}-\alpha)}=Q\sin{\alpha}\) এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে

 \(OC^{2}=OD^{2}+CD^{2} \Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(OC^{2}=OD^{2}+CD^{2} \Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
\(R\) যদি \(P\) এর দিকের সহিত \(θ\) কোণ উৎপন্ন করে অর্থাৎ \(\angle COD=\theta\) হলে,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA+AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA+AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
অতএব লব্ধির মান ও দিক যথাক্রমে \(R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\) ও \(\theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
সুতরাং \(\triangle{OAC}\) হতে পাই , \(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\)
\(\Rightarrow \overrightarrow{Oc}=\overrightarrow{OA}+\overrightarrow{OB}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\therefore \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)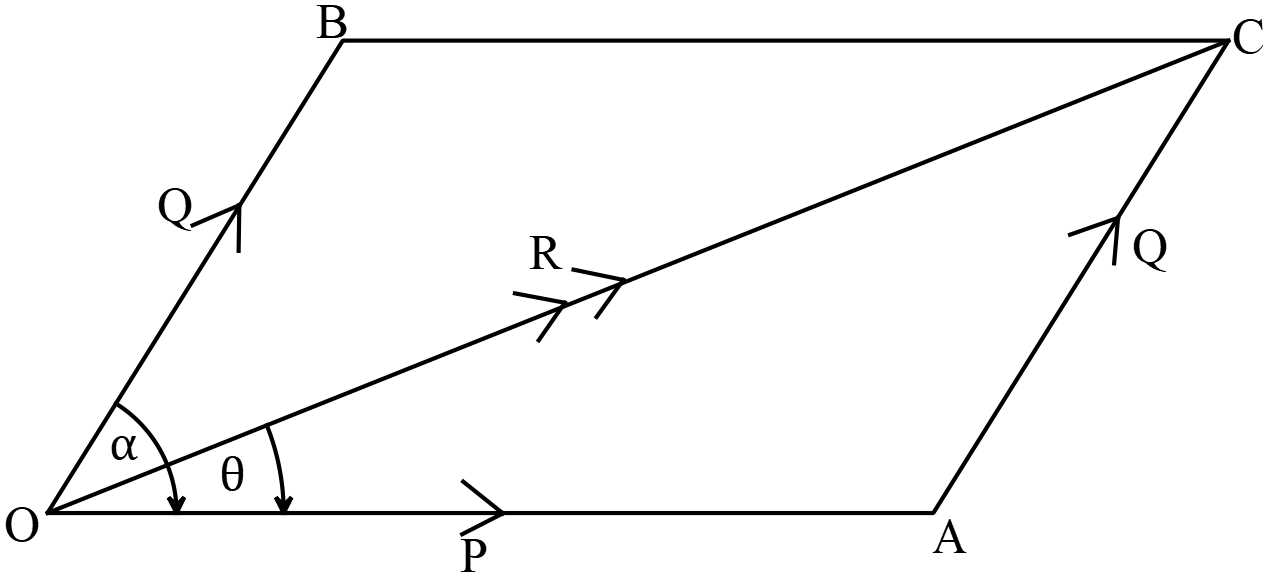
\(\Rightarrow \overrightarrow{R}.\overrightarrow{R}=(\overrightarrow{P}+\overrightarrow{Q}).(\overrightarrow{P}+\overrightarrow{Q})\)
\(\Rightarrow \overrightarrow{R}.\overrightarrow{R}=\overrightarrow{P}.\overrightarrow{P}+2\overrightarrow{P}.\overrightarrow{Q}+\overrightarrow{Q}.\overrightarrow{Q}\)
\(\Rightarrow R^2=P^2+2PQ\cos{\alpha}+Q^2\) ➜ \(\because \overrightarrow{v}.\overrightarrow{v}=v^2, \overrightarrow{u}.\overrightarrow{v}=uv\cos{\alpha}\)
\(\Rightarrow R^2=P^2+Q^2+2PQ\cos{\alpha}\)
\(\therefore R=\sqrt{P^2+Q^2+2PQ\cos{\alpha}}\)
যা বলদ্বয়ের লব্ধি নির্দেশ করে।
আবার,
\(\overrightarrow{P}.\overrightarrow{R}=\overrightarrow{P}.(\overrightarrow{P}+\overrightarrow{Q})\) ➜ \(\because \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)
\(\Rightarrow PR\cos{\theta}=\overrightarrow{P}.\overrightarrow{P}+\overrightarrow{P}.\overrightarrow{Q}\)
\(\Rightarrow PR\cos{\theta}=P^2+PQ\cos{\alpha}\) ➜ \(\because \overrightarrow{v}.\overrightarrow{v}=v^2, \overrightarrow{u}.\overrightarrow{v}=uv\cos{\alpha}\)
\(\Rightarrow PR\cos{\theta}=P(P+Q\cos{\alpha})\)
\(\therefore R\cos{\theta}=P+Q\cos{\alpha} ......(1)\) ➜ উভয় পার্শে \(P\) ভাগ করে।
এবং \(\overrightarrow{P}\times{\overrightarrow{R}}=\overrightarrow{P}\times{(\overrightarrow{P}+\overrightarrow{Q})}\) ➜ \(\because \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)
\(\Rightarrow \overrightarrow{P}\times{\overrightarrow{R}}=\overrightarrow{P}\times{\overrightarrow{P}}+\overrightarrow{P}\times{\overrightarrow{Q}}\)
\(\Rightarrow \hat{n}PR\sin{\theta}=0+\hat{n}PQ\sin{\alpha}\) ➜ \(\because \overrightarrow{u}\times{\overrightarrow{v}}=\hat{n}uv\sin{\alpha}, \overrightarrow{v}\times{\overrightarrow{v}}=0\)
\(\Rightarrow \hat{n}PR\sin{\theta}=\hat{n}PQ\sin{\alpha}\)
\(\therefore R\sin{\theta}=Q\sin{\alpha} ......(2)\) ➜ উভয় পার্শে \(\hat{n}P\) ভাগ করে।
\((2)\div{(1)}\) এর সাহায্যে
\(\frac{R\sin{\theta}}{R\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
যা লব্ধির দিক নির্দেশ করে।
লব্ধির মান ও দিক নির্ণয়ঃ মনে করি \(O\) বিন্দতে \(α\) কোণে ক্রিয়াশীল দুইটি বল \(P\) ও \(Q\) এর মান ও দিক যথাক্রমে \(OA\) এবং \(OB\) বাহু দ্বারা সূচিত হয়েছে। \(OACB\) সামান্তরিকটি অংকন করি। তাহলে বলের সামান্তরিক সুত্রানুসারে \(OC\) কর্ণটি ঐ বলদ্বয়ের লব্ধি \(R\) বলের মান ও দিক সূচিত করবে।
\((i)\) নং চিত্রে, \(OA\) এর বর্ধিতাংশের উপর \(CD\) লম্ব অংকন করি।
এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে

\(OC^{2}=OD^{2}+CD^{2}\Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
\(R\) যদি \(P\) এর দিকের সহিত \(θ\) কোণ উৎপন্ন করে অর্থাৎ \(\angle COD=\theta\) হলে,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA+AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA+AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\) \((ii)\) নং চিত্রে, \(OA\) এর উপর \(CD\) লম্ব অংকন করি।
এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে

\(OC^{2}=OD^{2}+CD^{2}\Rightarrow OC^{2}=\left\{OA-AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA-AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(\Rightarrow OC^{2}=\left\{OA-AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P-Q\cos{(180^{o}-\alpha)}\right\}^{2}+\left\{Q\sin{(180^{o}-\alpha)}\right\}^{2}\)
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
আবার,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA-AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA-AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{(180^{o}-\alpha)}}{P+Q\cos{(180^{o}-\alpha)}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
অতএব লব্ধির মান ও দিক যথাক্রমে \(R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\) ও \(\theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
আবার,
যদি বল \(Q\) এর সাথে লব্ধি \(\beta\) কোন উৎপন্ন করে সেই ক্ষেত্রে লদ্ধির দিক হবে নিম্নুরুপ
\(\beta=\tan^{-1}\left(\frac{P\sin{\alpha}}{Q+P\cos{\alpha}}\right)\)
বিকল্প পদ্ধতিঃ
\((i)\) নং চিত্রে, \(OA\) এর বর্ধিতাংশের উপর অথবা \((ii)\) নং চিত্রে, \(OA\) এর উপর লম্ব অংকন করি।এখন \((i)\) নং চিত্রে,\(AD=AC\frac{AD}{AC}=AC.\cos{\angle CAD}=Q\cos{\alpha}\) এবং \(CD=AC\frac{CD}{AC}=AC.\cos{\angle CAD}=Q\sin{\alpha}\)
\(\therefore OD=OA+AD=P+Q\cos{\alpha}\)
\((ii)\) নং চিত্রে,\(AD=AC\frac{AD}{AC}=AC.\cos{\angle CAD}=Q\cos{(180^{o}-\alpha)}=-Q\cos{\alpha}\)
\(\therefore OD=OA-AD=P+Q\cos{\alpha}\)
এবং \(CD=AC\frac{CD}{AC}=AC.\sin{\angle CAD}=Q\sin{(180^{o}-\alpha)}=Q\sin{\alpha}\) এক্ষণে, \(OCD\) সমকোণী ত্রিভুজ থেকে

 \(OC^{2}=OD^{2}+CD^{2} \Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)
\(OC^{2}=OD^{2}+CD^{2} \Rightarrow OC^{2}=\left\{OA+AD\right\}^{2}+CD^{2}\)
\(\Rightarrow OC^{2}=\left\{OA+AC.\frac{AD}{AC}\right\}^{2}+\left\{AC\frac{CD}{AC}\right\}^{2}\)\(\Rightarrow OC^{2}=\left\{OA+AC.\cos{\angle CAD}\right\}^{2}+\left\{AC.\sin{\angle CAD}\right\}^{2}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\Rightarrow R^{2}=\left\{P+Q\cos{\alpha}\right\}^{2}+\left\{Q\sin{\alpha}\right\}^{2}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\cos^{2}{\alpha}+Q^{2}\sin^{2}{\alpha}\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\left(\cos^{2}{\alpha}+\sin^{2}{\alpha}\right)\)
\(\Rightarrow R^{2}=P^{2}+2PQ\cos{\alpha}+Q^{2}\)
\(\Rightarrow R^{2}=P^{2}+Q^{2}+2PQ\cos{\alpha}\)
\(\Rightarrow R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
\(R\) যদি \(P\) এর দিকের সহিত \(θ\) কোণ উৎপন্ন করে অর্থাৎ \(\angle COD=\theta\) হলে,
\(\tan\theta=\frac{CD}{OD}=\frac{CD}{OA+AD}\)
\(=\frac{AC.\frac{CD}{AC}}{OA+AC.\frac{AD}{AC}}\)
\(=\frac{Q\sin{\angle CAD}}{P+Q\cos{\angle CAD}}\)
\(=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
অতএব লব্ধির মান ও দিক যথাক্রমে \(R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\) ও \(\theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
ভেক্টর পদ্ধতিঃ
এখানে \(P, Q\) ও \(R\) বলতিনটির প্রত্যেকেই ভেক্টর এবং যথাক্রমে \(\overrightarrow{OA}, \overrightarrow{OB}\) ও \(\overrightarrow{OC}\) দ্বারা সূচিত।সুতরাং \(\triangle{OAC}\) হতে পাই , \(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\)
\(\Rightarrow \overrightarrow{Oc}=\overrightarrow{OA}+\overrightarrow{OB}\) ➜ \(OB\) ও \(AC\) রেখা সমান ও সমান্তরাল
\(\therefore \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)

\(\Rightarrow \overrightarrow{R}.\overrightarrow{R}=(\overrightarrow{P}+\overrightarrow{Q}).(\overrightarrow{P}+\overrightarrow{Q})\)
\(\Rightarrow \overrightarrow{R}.\overrightarrow{R}=\overrightarrow{P}.\overrightarrow{P}+2\overrightarrow{P}.\overrightarrow{Q}+\overrightarrow{Q}.\overrightarrow{Q}\)
\(\Rightarrow R^2=P^2+2PQ\cos{\alpha}+Q^2\) ➜ \(\because \overrightarrow{v}.\overrightarrow{v}=v^2, \overrightarrow{u}.\overrightarrow{v}=uv\cos{\alpha}\)
\(\Rightarrow R^2=P^2+Q^2+2PQ\cos{\alpha}\)
\(\therefore R=\sqrt{P^2+Q^2+2PQ\cos{\alpha}}\)
যা বলদ্বয়ের লব্ধি নির্দেশ করে।
আবার,
\(\overrightarrow{P}.\overrightarrow{R}=\overrightarrow{P}.(\overrightarrow{P}+\overrightarrow{Q})\) ➜ \(\because \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)
\(\Rightarrow PR\cos{\theta}=\overrightarrow{P}.\overrightarrow{P}+\overrightarrow{P}.\overrightarrow{Q}\)
\(\Rightarrow PR\cos{\theta}=P^2+PQ\cos{\alpha}\) ➜ \(\because \overrightarrow{v}.\overrightarrow{v}=v^2, \overrightarrow{u}.\overrightarrow{v}=uv\cos{\alpha}\)
\(\Rightarrow PR\cos{\theta}=P(P+Q\cos{\alpha})\)
\(\therefore R\cos{\theta}=P+Q\cos{\alpha} ......(1)\) ➜ উভয় পার্শে \(P\) ভাগ করে।
এবং \(\overrightarrow{P}\times{\overrightarrow{R}}=\overrightarrow{P}\times{(\overrightarrow{P}+\overrightarrow{Q})}\) ➜ \(\because \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\)
\(\Rightarrow \overrightarrow{P}\times{\overrightarrow{R}}=\overrightarrow{P}\times{\overrightarrow{P}}+\overrightarrow{P}\times{\overrightarrow{Q}}\)
\(\Rightarrow \hat{n}PR\sin{\theta}=0+\hat{n}PQ\sin{\alpha}\) ➜ \(\because \overrightarrow{u}\times{\overrightarrow{v}}=\hat{n}uv\sin{\alpha}, \overrightarrow{v}\times{\overrightarrow{v}}=0\)
\(\Rightarrow \hat{n}PR\sin{\theta}=\hat{n}PQ\sin{\alpha}\)
\(\therefore R\sin{\theta}=Q\sin{\alpha} ......(2)\) ➜ উভয় পার্শে \(\hat{n}P\) ভাগ করে।
\((2)\div{(1)}\) এর সাহায্যে
\(\frac{R\sin{\theta}}{R\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \frac{\sin{\theta}}{\cos{\theta}}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\Rightarrow \tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\therefore \theta=\tan^{-1}\left(\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\right)\)
যা লব্ধির দিক নির্দেশ করে।
×
এক বিন্দুতে নির্দিষ্ট কোণে ক্রিয়ারত দুইটি বলের লব্ধির বৃহত্তম ও ক্ষুদ্রতম মান নির্ণয় কর।
উত্তরঃ লব্ধির বৃহত্তম মান \(R_{max}=P+Q\)
লব্ধির ক্ষুদ্রতম মান \(R_{min}=P-Q\)
উত্তরঃ লব্ধির বৃহত্তম মান \(R_{max}=P+Q\)
লব্ধির ক্ষুদ্রতম মান \(R_{min}=P-Q\)
সমাধানঃ
আমরা জানি \(R=\sqrt{P^{2}+Q^{2}+2PQ\cos{\alpha}}\)
লব্ধি বৃহত্তম হবে, যখন \(\alpha=0^{০} \)
বৃহত্তম লব্ধি \(R_{max}=\sqrt{P^{2}+Q^{2}+2PQ\cos{0^{o}}}\)
\(=\sqrt{P^{2}+Q^{2}+2PQ}\) ➜ \(\because \cos{0^{o}}=1\)
\(=\sqrt{(P+Q)^{2}}\)
\(=(P+Q)\)
লব্ধি ক্ষুদ্রতম হবে, যখন \(\alpha=180^{০} \)
ক্ষুদ্রতম লব্ধি \(R_{min}=\sqrt{P^{2}+Q^{2}+2PQ\cos{180^{o}}}\)
\(=\sqrt{P^{2}+Q^{2}-2PQ}\) ➜ \(\because \cos{180^{o}}=-1\)
\(=\sqrt{(P-Q)^{2}}\)
\(=(P-Q)\) ➜ \(p>Q\)
অতএব বৃহত্তম ও ক্ষুদ্রতম লব্ধি যথাক্রমে,
\(R_{max}=P+Q\) ও \(R_{min}=P-Q\)
লব্ধি বৃহত্তম হবে, যখন \(\alpha=0^{০} \)
বৃহত্তম লব্ধি \(R_{max}=\sqrt{P^{2}+Q^{2}+2PQ\cos{0^{o}}}\)
\(=\sqrt{P^{2}+Q^{2}+2PQ}\) ➜ \(\because \cos{0^{o}}=1\)
\(=\sqrt{(P+Q)^{2}}\)
\(=(P+Q)\)
লব্ধি ক্ষুদ্রতম হবে, যখন \(\alpha=180^{০} \)
ক্ষুদ্রতম লব্ধি \(R_{min}=\sqrt{P^{2}+Q^{2}+2PQ\cos{180^{o}}}\)
\(=\sqrt{P^{2}+Q^{2}-2PQ}\) ➜ \(\because \cos{180^{o}}=-1\)
\(=\sqrt{(P-Q)^{2}}\)
\(=(P-Q)\) ➜ \(p>Q\)
অতএব বৃহত্তম ও ক্ষুদ্রতম লব্ধি যথাক্রমে,
\(R_{max}=P+Q\) ও \(R_{min}=P-Q\)
×
একই বিন্দুতে ক্রিয়াশীল দুইটি বলের মান ও দিক কোন ত্রিভুজের একইক্রমে গ্রিহীত দুইটি বাহু দ্বারা সূচিত হলে, তাদের লব্ধির মান ও দিক ঐ ত্রিভুজের বিপরীতক্রমে গৃহীত তৃতীয় বাহু দ্বারা সূচিত হবে।
Proof:
মনে করি, একই বিন্দুতে ক্রিয়াশীল দুইটি বলের মান ও দিক যথাক্রমে \(OAB\) ত্রিভুজের \(OA\) এবং \(AB\) বাহু দ্বারা সূচিত হল। তাহলে তাদের লব্ধির মান ও দিক বিপরীতক্রমে গৃহীত তৃতীয় বাহু \(OB\) দ্বারা সূচিত হবে।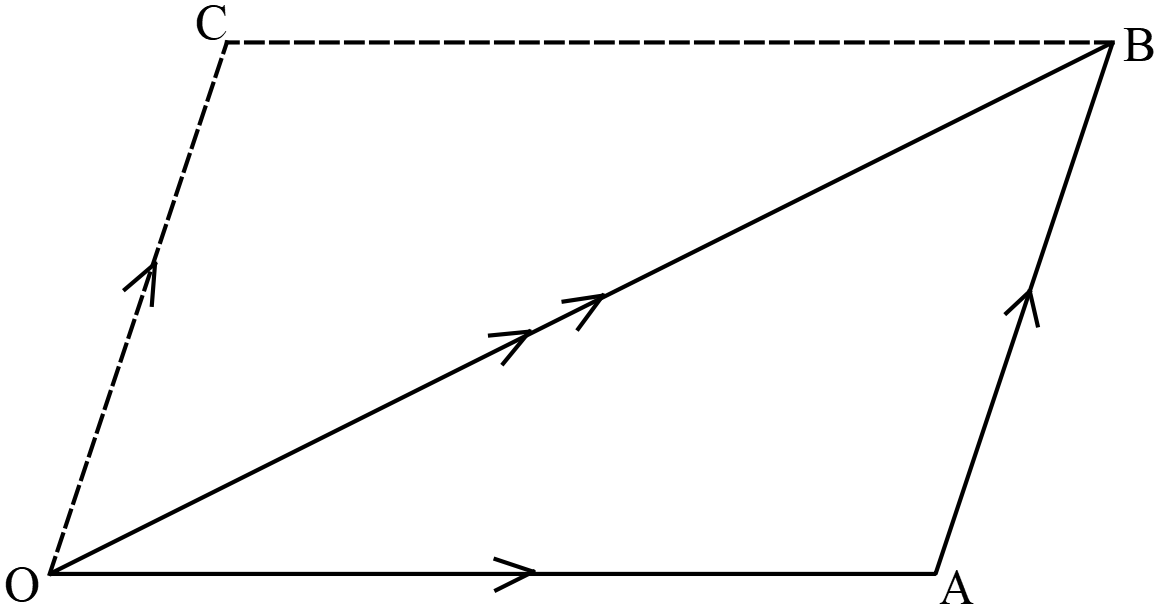
\(OABC\) সামান্তরিক অংকন করি। বলের সামান্তরিক সূত্রানুসারে \(OA\) এবং \(OC\) বাহু দ্বারা সূচিত বলদ্বয়ের লব্ধি \(OB\) দ্বারা সূচিত হবে। কিন্তু \(AB\) ও \(OC\) সমান ও সমান্তরাল বলে তারা একই বল সুচীত করে।
অতএব \(OA\) এবং \(AB\) বাহু দ্বারা সূচিত বলদ্বয়ের লব্ধি \(OB\) দ্বারা সূচিত হবে।
ভেক্টরের সাহায্যে \(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)

\(OABC\) সামান্তরিক অংকন করি। বলের সামান্তরিক সূত্রানুসারে \(OA\) এবং \(OC\) বাহু দ্বারা সূচিত বলদ্বয়ের লব্ধি \(OB\) দ্বারা সূচিত হবে। কিন্তু \(AB\) ও \(OC\) সমান ও সমান্তরাল বলে তারা একই বল সুচীত করে।
অতএব \(OA\) এবং \(AB\) বাহু দ্বারা সূচিত বলদ্বয়ের লব্ধি \(OB\) দ্বারা সূচিত হবে।
ভেক্টরের সাহায্যে \(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
×
একই বিন্দুতে ক্রিয়াশীল \((n-1)\) সংখ্যক বলের মান ও দিক কোন n সংখ্যক বাহুবিশিষ্ট বহুভুজের একইক্রমে গ্রিহীত \((n-1)\) সংখ্যক বাহু দ্বারা সূচিত হলে, তাদের লব্ধির মান ও দিক ঐ বহুভুজের বিপরীতক্রমে গৃহীত \(n\) তম বাহু দ্বারা সূচিত হবে।
Proof:
মনে করি, একই বিন্দুতে ক্রিয়াশীল পাঁচটি বলের মান ও দিক যথাক্রমে ABCDEF বহুভুজের একইক্রমে গৃহীত \(AB,BC,CD,DE\) এবং \(EF\) বাহু দ্বারা সূচিত হল। তাহলে তাদের লব্ধির মান ও দিক বিপরীতক্রমে গৃহীত তৃতীয় বাহু \(AF\) দ্বারা সূচিত হবে। 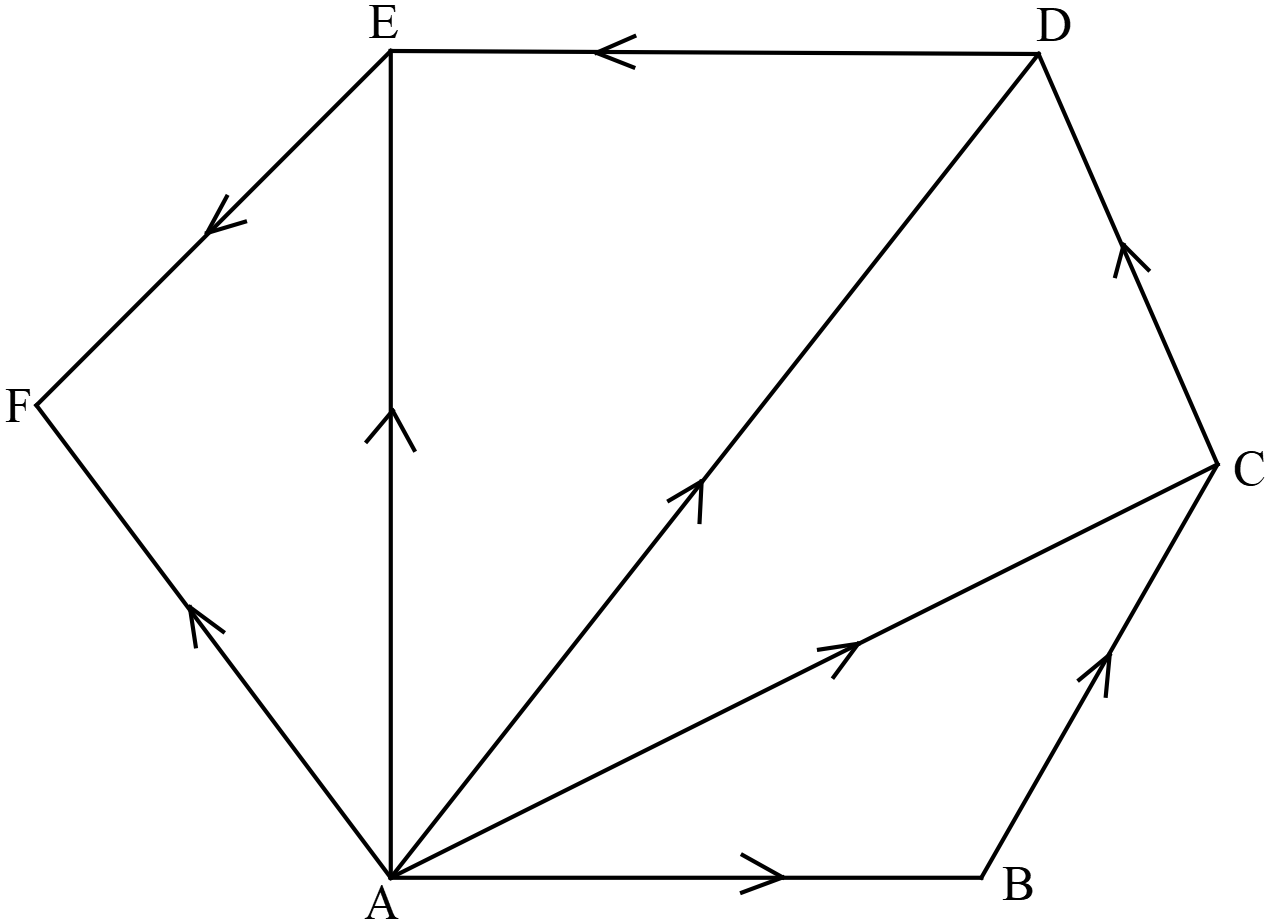
\(AC,AD,AE\) সংযুক্ত কুরি। বল সংযোজনের ত্রিভুজ সূত্রানুসারে \(AB\) এবং \(BC\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \(AC\) দ্বারা সূচিত হবে।
অনুরূপে \(AC\) এবং \(CD\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \(AD\) দ্বারা সূচিত হবে। \(AD\) ও \(DE\) এর লব্ধি \(AE\) এবং \(AE\) ও \(EF\) এর লব্ধি \(AF\) দ্বারা সূচিত হবে। সুতরাং বলগুলোর সকলের লব্ধি \(AF\) দ্বারা সুচিত হবে।
ভেক্টরের সাহায্যে সুচিত করলে, \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{AF}\)

\(AC,AD,AE\) সংযুক্ত কুরি। বল সংযোজনের ত্রিভুজ সূত্রানুসারে \(AB\) এবং \(BC\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \(AC\) দ্বারা সূচিত হবে।
অনুরূপে \(AC\) এবং \(CD\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \(AD\) দ্বারা সূচিত হবে। \(AD\) ও \(DE\) এর লব্ধি \(AE\) এবং \(AE\) ও \(EF\) এর লব্ধি \(AF\) দ্বারা সূচিত হবে। সুতরাং বলগুলোর সকলের লব্ধি \(AF\) দ্বারা সুচিত হবে।
ভেক্টরের সাহায্যে সুচিত করলে, \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{AF}\)
×
প্রমান কর যে, কোন \(O\) বিন্দুতে \(OA\) এবং \(AB\) রেখা বরাবর ক্রিয়াশীল দুইটি বলের মান যথাক্রমে \(m.OA\) এবং \(n.OB\) দ্বারা সূচিত হলে, উক্ত বলদ্বয়ের লব্ধির মান ও দিক \((m+n)OC\) দ্বারা সূচিত হবে, \(C\) বিন্দুটি \(AB\) এর উপর এমনভাবে অবস্থিত হবে যে, \(m.AC=n.BC\) হবে; অর্থাৎ \(C\) বিন্দুটি \(AB\) রেখাকে \(n:m\) অনুপাতে অন্তর্বিভক্ত করবে।
Proof:
\(AB\) যোগ করি এবং এর উপর এমন একটি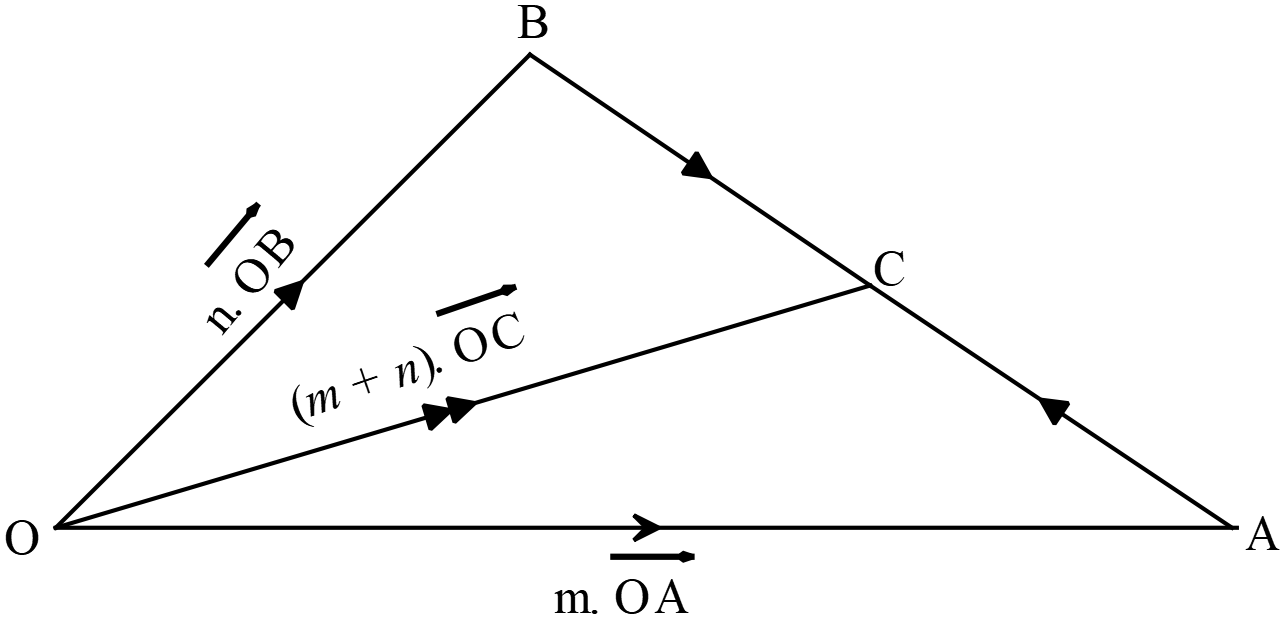
\(C\) বিন্দু নেই যেন \(m.AC=n.BC\) হয়। \(OC\) যোগ করি; তাহলে বলগুলো একই বিন্দুতে ক্রিয়াশীল মনে করে ( বল সংযোজনের ত্রিভুজ সূত্রানুসারে ) ভেক্টরের সাহায্যে \(OAC\) ত্রিভুজ থেকে, \(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\).
\(\Rightarrow m\overrightarrow{OA}+m\overrightarrow{AC}=m\overrightarrow{OC}\) ........(i)
অনুরূপভাবে,
\(OBC\) ত্রিভুজ থেকে,\(\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}\).
\(\Rightarrow n\overrightarrow{OB}+n\overrightarrow{BC}=n\overrightarrow{OC}\) ........(ii)
\((i)\) এবং \((ii)\) যোগ করে,
\(\Rightarrow m\overrightarrow{OA}+m\overrightarrow{AC}+n\overrightarrow{OB}+n\overrightarrow{BC}=m\overrightarrow{OC}+n\overrightarrow{OC}\)
কিন্তু \(\overrightarrow{AC}\) ও \(n\overrightarrow{BC}\) বলদ্বয়ের মান সমান ও তারা বিপরীতমূখী বলে একে অপরের ক্রিয়া বিনাশ করে।
\(\therefore m\overrightarrow{OA}+n\overrightarrow{OB}=(m+n)\overrightarrow{OC}\)
সুতরাং \(m\overrightarrow{OA}\) ও \(n\overrightarrow{OB}\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \((m+n)\overrightarrow{OC}\) দ্বারা সূচিত হবে।

\(C\) বিন্দু নেই যেন \(m.AC=n.BC\) হয়। \(OC\) যোগ করি; তাহলে বলগুলো একই বিন্দুতে ক্রিয়াশীল মনে করে ( বল সংযোজনের ত্রিভুজ সূত্রানুসারে ) ভেক্টরের সাহায্যে \(OAC\) ত্রিভুজ থেকে, \(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\).
\(\Rightarrow m\overrightarrow{OA}+m\overrightarrow{AC}=m\overrightarrow{OC}\) ........(i)
অনুরূপভাবে,
\(OBC\) ত্রিভুজ থেকে,\(\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}\).
\(\Rightarrow n\overrightarrow{OB}+n\overrightarrow{BC}=n\overrightarrow{OC}\) ........(ii)
\((i)\) এবং \((ii)\) যোগ করে,
\(\Rightarrow m\overrightarrow{OA}+m\overrightarrow{AC}+n\overrightarrow{OB}+n\overrightarrow{BC}=m\overrightarrow{OC}+n\overrightarrow{OC}\)
কিন্তু \(\overrightarrow{AC}\) ও \(n\overrightarrow{BC}\) বলদ্বয়ের মান সমান ও তারা বিপরীতমূখী বলে একে অপরের ক্রিয়া বিনাশ করে।
\(\therefore m\overrightarrow{OA}+n\overrightarrow{OB}=(m+n)\overrightarrow{OC}\)
সুতরাং \(m\overrightarrow{OA}\) ও \(n\overrightarrow{OB}\) দ্বারা সূচিত বলদ্বয়ের লব্ধি \((m+n)\overrightarrow{OC}\) দ্বারা সূচিত হবে।
×
কোন বিন্দুতে ক্রিয়ারত দুইটি বলের কোন নির্দিষ্ট দিকের লম্বাংশের বীজগাণিতিক যোগফল তাদের লব্ধির উক্ত দিকের লম্বাংশের সমান।
Proof:
মনে করি, \(OA\) এবং \(OB\) রেখাদ্বয় যথাক্রমে \(O\) বিন্দুতে ক্রিয়ারত \(P\) ও \(Q\) বলদ্বয়কে সূচিত করেছে। তাহলে \(OACB\) সামান্তরিকের \(OC\) কর্ণ দ্বারা তাদের লব্ধি \(R\) সূচিত হবে।
মনে করি, \(OX\) রেখাটি নির্দিষ্ট দিক নির্দেশ করে। \(OX\) এর উপর \(AL, BM, CN\) লম্ব টানি। তাহলে \(OX\) বরাবর \(P, Q, R\) বলের লম্বাংশ যথাক্রমে \(OL, OM, ON\) হবে।
প্রথম চিত্রে তারা সকলেই যোগবোধক এবং দ্বিতীয় চিত্রে, \(OM\) বিয়োগবোধক।
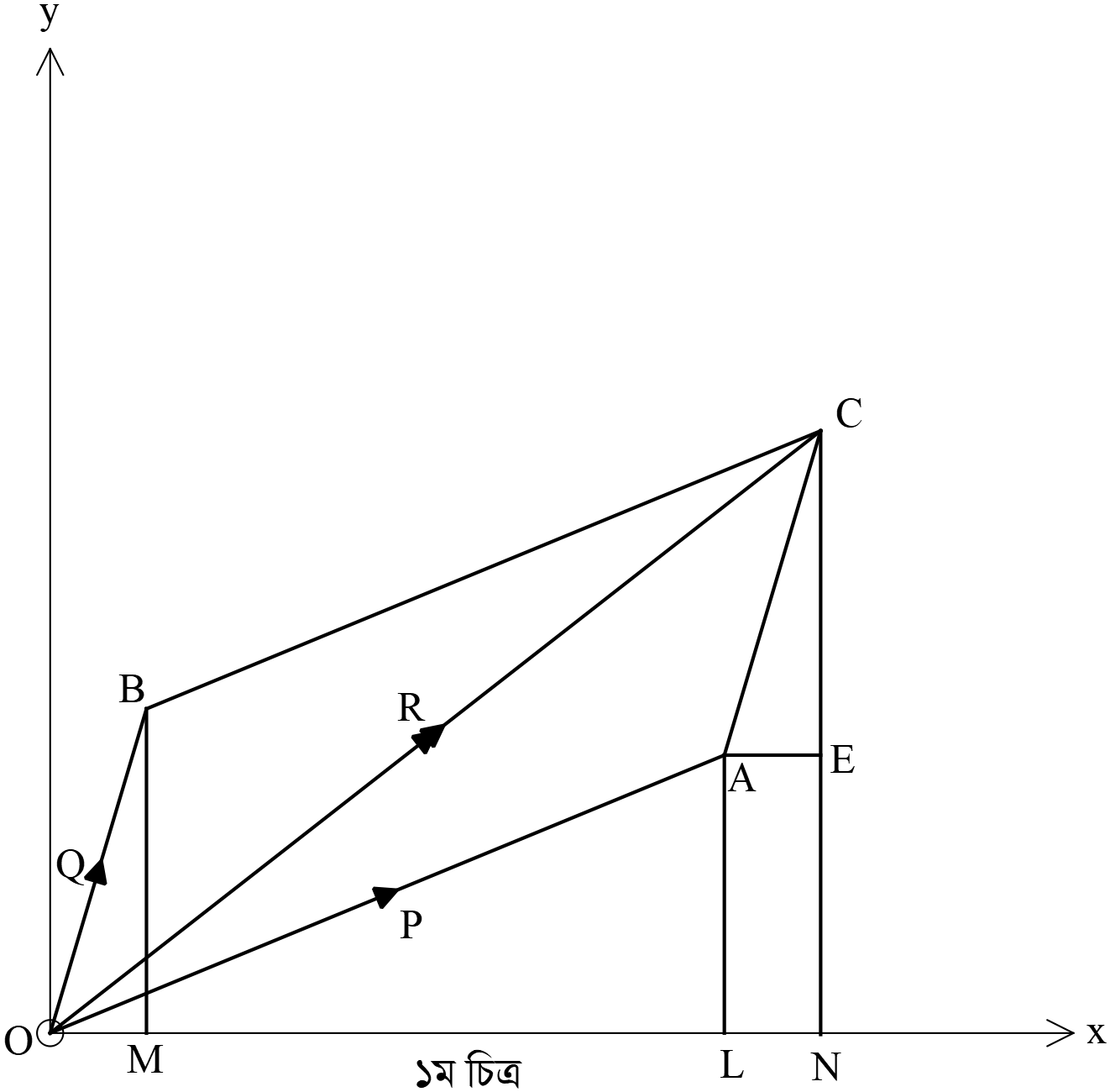
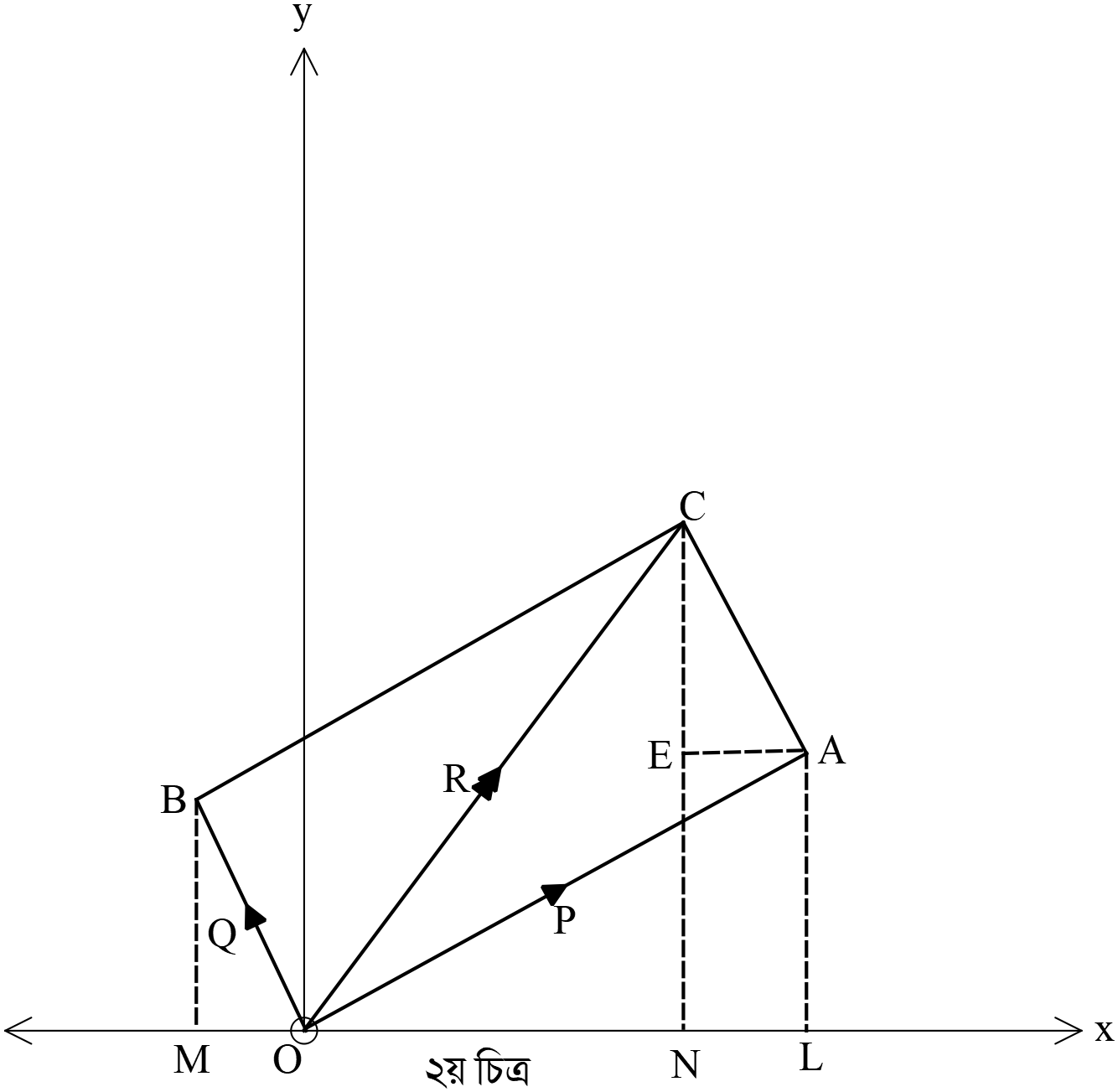 \(CN\) এর উপর \(AE\) লম্ব আঁকি। এক্ষণে \(OBM\) এবং \(CAE\) ত্রিভুজদ্বয়ের বাহুগুলি পরস্পর সমান্তরাল এবং \(OB\) ও \(AC\) এর দৈর্ঘ্য সমান। অতএব \(OM=AE=LN.\)
সুতরাং \(OX\) বরাবর \(P\) ও \(Q\) বলদ্বয়ের লম্বাংশের বীজগাণিতিক যোগফল,
\(CN\) এর উপর \(AE\) লম্ব আঁকি। এক্ষণে \(OBM\) এবং \(CAE\) ত্রিভুজদ্বয়ের বাহুগুলি পরস্পর সমান্তরাল এবং \(OB\) ও \(AC\) এর দৈর্ঘ্য সমান। অতএব \(OM=AE=LN.\)
সুতরাং \(OX\) বরাবর \(P\) ও \(Q\) বলদ্বয়ের লম্বাংশের বীজগাণিতিক যোগফল,
পথম চিত্রে,
\(OL+OM\)
\(=OL+LN\)
\(=ON\)
\(=OX\) বরাবর লব্ধি R এর লম্বাংশ।
দ্বিতীয় চিত্রে,
\(OL-OM\)
\(=OL-LN\)
\(=ON\)
\(=OX\) বরাবর লব্ধি R এর লম্বাংশ।
মনে করি, \(OX\) রেখাটি নির্দিষ্ট দিক নির্দেশ করে। \(OX\) এর উপর \(AL, BM, CN\) লম্ব টানি। তাহলে \(OX\) বরাবর \(P, Q, R\) বলের লম্বাংশ যথাক্রমে \(OL, OM, ON\) হবে।
প্রথম চিত্রে তারা সকলেই যোগবোধক এবং দ্বিতীয় চিত্রে, \(OM\) বিয়োগবোধক।

 \(CN\) এর উপর \(AE\) লম্ব আঁকি। এক্ষণে \(OBM\) এবং \(CAE\) ত্রিভুজদ্বয়ের বাহুগুলি পরস্পর সমান্তরাল এবং \(OB\) ও \(AC\) এর দৈর্ঘ্য সমান। অতএব \(OM=AE=LN.\)
সুতরাং \(OX\) বরাবর \(P\) ও \(Q\) বলদ্বয়ের লম্বাংশের বীজগাণিতিক যোগফল,
\(CN\) এর উপর \(AE\) লম্ব আঁকি। এক্ষণে \(OBM\) এবং \(CAE\) ত্রিভুজদ্বয়ের বাহুগুলি পরস্পর সমান্তরাল এবং \(OB\) ও \(AC\) এর দৈর্ঘ্য সমান। অতএব \(OM=AE=LN.\)
সুতরাং \(OX\) বরাবর \(P\) ও \(Q\) বলদ্বয়ের লম্বাংশের বীজগাণিতিক যোগফল,পথম চিত্রে,
\(OL+OM\)
\(=OL+LN\)
\(=ON\)
\(=OX\) বরাবর লব্ধি R এর লম্বাংশ।
দ্বিতীয় চিত্রে,
\(OL-OM\)
\(=OL-LN\)
\(=ON\)
\(=OX\) বরাবর লব্ধি R এর লম্বাংশ।
প্রয়োজনীয় সূত্রাবলী
Required formulas
পরস্পর \(\alpha\) কোণে একই সময়ে ক্রিয়াশীল দুইটি সমবিন্দু বল \(\bar{P}\) ও \(\bar{Q}\) এর লব্ধি \(\bar{R},\) যা \(\bar{P}\) এর সাথে \(\theta\) কোণ উৎপন্ন করে।
\(\bar{R}=\bar{P}+\bar{Q}\)
\(R^2=P^2+Q^2+2PQ\cos{\alpha}\)
\(Q^2=P^2+R^2-2PR\cos{\theta}\)
\(R\cos{\theta}=P+Q\cos{\alpha}\)
\(R\sin{\theta}=Q\sin{\alpha}\)
\(\frac{P}{\sin{(\alpha-\theta)}}=\frac{Q}{\sin{\theta}}=\frac{R}{\sin{\alpha}}\)
\(\tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\cot{\theta}=\frac{P+Q\cos{\alpha}}{Q\sin{\alpha}}\)
\(\alpha=90^{o}\) হলে,
\(R^2=P^2+Q^2\)
\(R\cos{\theta}=P\)
\(R\sin{\theta}=Q\)
\(\theta=\tan^{-1}{\left(\frac{Q}{P}\right)}\)
\(\theta=90^{o}\) হলে,
\(Q^2=P^2+R^2\)
\(P+Q\cos{\alpha}=0\)
\(R=Q\sin{\alpha}\)
\(R\) বলের দুই পার্শ্বে তার সাথে যথাক্রমে \(\alpha\) ও \(\beta\) কোণে কার্যরত অংশকদ্বয় \(P\) ও \(Q\) হলে,
\(P=\frac{R\sin{\beta}}{\sin{(\alpha+\beta)}}\)
\(Q=\frac{R\sin{\alpha}}{\sin{(\alpha+\beta)}}\)
\(\bar{R}=\bar{P}+\bar{Q}\)
\(R^2=P^2+Q^2+2PQ\cos{\alpha}\)
\(Q^2=P^2+R^2-2PR\cos{\theta}\)
\(R\cos{\theta}=P+Q\cos{\alpha}\)
\(R\sin{\theta}=Q\sin{\alpha}\)
\(\frac{P}{\sin{(\alpha-\theta)}}=\frac{Q}{\sin{\theta}}=\frac{R}{\sin{\alpha}}\)
\(\tan{\theta}=\frac{Q\sin{\alpha}}{P+Q\cos{\alpha}}\)
\(\cot{\theta}=\frac{P+Q\cos{\alpha}}{Q\sin{\alpha}}\)
\(\alpha=90^{o}\) হলে,
\(R^2=P^2+Q^2\)
\(R\cos{\theta}=P\)
\(R\sin{\theta}=Q\)
\(\theta=\tan^{-1}{\left(\frac{Q}{P}\right)}\)
\(\theta=90^{o}\) হলে,
\(Q^2=P^2+R^2\)
\(P+Q\cos{\alpha}=0\)
\(R=Q\sin{\alpha}\)
\(R\) বলের দুই পার্শ্বে তার সাথে যথাক্রমে \(\alpha\) ও \(\beta\) কোণে কার্যরত অংশকদ্বয় \(P\) ও \(Q\) হলে,
\(P=\frac{R\sin{\beta}}{\sin{(\alpha+\beta)}}\)
\(Q=\frac{R\sin{\alpha}}{\sin{(\alpha+\beta)}}\)
উদাহরণসমুহ
\(Ex.1.\) \(O\) বিন্দুতে যুগপৎ ক্রিয়ারত \(P\) ও \(Q\) বল দুইটি যথাক্রমে \(OA\) ও \(OB\) রেখাংশ দ্বারা সূচিত। \(P=160 \ lb.wt, \ Q=100 \ lb.wt\) এবং \(OA=8 cm\) হলে \(OB\) রেখাংশের দৈর্ঘ্য কত?
উত্তরঃ \(5 cm\)
উত্তরঃ \(5 cm\)
\(Ex.2.\) কোন বিন্দুতে ক্রিয়ারত \(3P\) এবং \(2P\) মানের দুইটি বলের লব্ধি \(R;\) প্রথম বলটির মান দ্বিগুন করলে লব্ধির মানও দ্বিগুন হয়। বলদ্বয়ের অন্তর্গত কোণ নির্ণয় কর।
উত্তরঃ \(120^{o}\)
উত্তরঃ \(120^{o}\)
রাঃ,যঃ ২০০৩; বঃ ২০০৩; কুঃ,সিঃ ২০০৭; বুয়েটঃ ২০০৩-২০০৪; ডুয়েটঃ ২০১৪-২০১৫
\(Ex.3.\) কোনো বিন্দুতে ক্রিয়ারত দুইটি বলের বৃহত্তম ও ক্ষুদ্রতম লব্ধির মান যথাক্রমে \(F\) ও \(G\)। প্রমাণ কর যে, বলদ্বয়ের ক্রিয়ারেখার মধ্যবর্তী কোণ \(\alpha\) হলে তাদের লব্ধির মান \(\sqrt{F^2\cos^2{\frac{\alpha}{2}}+G^2\sin^2{\frac{\alpha}{2}}}\) হবে।
দিঃ ২০১২; যঃ ২০১৪,২০১৯; রাঃ ২০২১
\(Ex.4.\) একটি বিন্দুতে কার্যরত \(P\) ও \(Q\) বলের লব্ধি \(R; \ P\) বলকে দ্বিগুণ করলে নতুন লব্ধি \(P\) বলের ক্রিয়া রেখার উপর লম্ব হয়। প্রমাণ কর যে, \(Q=R\)
\(Ex.5.\) কোন বিন্দুতে \(P\) এবং \(2P\) মানের দুইটি বল ক্রিয়াশীল। প্রথমটিকে দ্বিগুণ করে দ্বিতীয়টির মাণ \(8\) একক বৃদ্ধি করলে লব্ধির দিক অপরিবর্তিত থাকে। \(P\) এর মাণ নির্ণয় কর।
উত্তরঃ \(4\) একক।
উত্তরঃ \(4\) একক।
ঢাঃ ২০০০; রাঃ ২০১১; কুয়েটঃ ২০০৮-২০০৯; চুয়েটঃ ২০১১-২০১২
\(Ex.6.\) কোনো বিন্দুতে \(2\alpha\) কোণে ক্রিয়ারত \(P+Q\) এবং \(P-Q\) মানের বল দুইটির লব্ধি এদের অন্তর্গত কোণের সমদ্বিখন্ডকের সাথে \(\theta\) কোণ উৎপন্ন করে। দেখাও যে, \(P\tan{\theta}=Q\tan{\alpha}\)
ঢাঃ ২০০৪,২০২১; রাঃ ২০০৯; চঃ ২০২১
\(Ex.7.\) \(P\) বলের উপাংশদ্বয় বিপরীত দিকে \(P\) এর সাথে \(15^{o}\) ও \(45^{o}\) কোণ উৎপন্ন করে। উপাংশদ্বয়ের মান নির্ণয় কর।
\(Ex.8.\) \(O\) বিন্দুতে ক্রিয়াশীল \(4P, \ 3P\) মানের বল দুইটির লব্ধির মান \(5P\) । যদি কোনো ছেদক তাদের ক্রিয়ারেখাকে যথাক্রমে \(R, \ S\) ও \(T\) বিন্দুতে ছেদ করে, তাহলে প্রমাণ কর যে, \(\frac{4}{OR}+\frac{3}{OS}=\frac{5}{OT}\)
বঃ ২০০২; রাঃ ২০০৭; চঃ ২০০৮,২০১৩; সিঃ ২০০৯,২০১৪; কুঃ ২০১১; দিঃ ২০১৩
\(Ex.9.\) কোন বিন্দুতে কিয়ারত \(P\) এবং \(Q\) বলদ্বয়ের লব্ধি \(R\) এর লম্বাংশ \(Q\) হলে দেখাও যে, বলদ্বয়ের অন্তর্গত কোণ \(\alpha=2\sin^{-1}\left(\sqrt{\frac{P}{2Q}}\right)=\cos^{-1}\left(\frac{Q-P}{Q}\right)\) এবং \(R=\sqrt{Q^2-P^2+2PQ}.\)
দিঃ ২০১৬; যঃ ২০১৩,২০০৮; রাঃ ২০১৩,২০২১; কুঃ ২০০৮; চঃ ২০০১; সিঃ ২০০২; মাঃ ২০১৩
\(Ex.10.\) কোনো বিন্দুতে ক্রিয়ারত \(Q-R, Q, Q+R\) মাণের বলগুলির দিক একইক্রমে কোনো সমবাহু ত্রিভুজের বাহুগুলির সমান্তরাল। বলগুলির লব্ধির মাণ ও দিক নির্ণয় কর।
উত্তরঃ \(\sqrt{3}R; Q-R\) বলের সাথে \(210^{o}\)
উত্তরঃ \(\sqrt{3}R; Q-R\) বলের সাথে \(210^{o}\)
যঃ ২০০৪; ঢাঃ ২০০১; কুঃ ২০২১
\(Ex.11.\) \(\triangle{ABC}\) এর সমতলে \(O\) একটি বিন্দু। \(BC, \ CA, \ AB\) বাহুগুলির মধ্যবিন্দু যথাক্রমে \(D, \ E, \ F\) হলে, প্রমাণ কর যে, \(\overline{OD}, \ \overline{OF}\) এবং \(\overline{EO}\) বলগুলির লব্ধি \(\overline{OB}.\)
সিঃ ২০০১
\(Ex.12.\) \(\theta\) কোণে ক্রিয়ারত \(P, Q\) মানের বলদ্বয়ের লব্ধি \((2m+1)\sqrt{P^{2}+Q^{2}}\), উক্ত কোণটি (\(90^{o}-\theta\)) হলে লব্ধির মান \((2m-1)\sqrt{P^{2}+Q^{2}}\) হয়। প্রমাণ কর যে, \(\tan\theta=\frac{m-1}{m+1}\).
দিঃ ২০১৫; ঢাঃ ২০১২,২০০৮;রাঃ ২০০৬,২০০৯; কুঃ ২০০০; মাঃ ২০১২
\(Ex.13.\) কোন বিন্দুতে কিয়ারত \(P\) এবং \(Q\) মানের দুইটি বলের লব্ধি তাদের অন্তর্গত কোণকে এক তৃতীয়াংশে বিভক্ত করে। দেখাও যে, তাদের অন্তর্গত কোণের পরিমাণ \(3\cos^{-1}{\left(\frac{P}{2Q}\right)}\) এবং লব্ধির মান \(\frac{P^{2}-Q^{2}}{Q}\) \(\left(P\gt{Q}\right)\).
ঢাঃ ২০১৬,২০১৩; সিঃ ২০১৫,২০০৮; দিঃ ২০১৪; মাঃ ২০১১; যঃ ২০১২,২০০৬; বঃ ২০০৩; কুঃ ২০১০,২০০১; রাঃ ২০০৮,২০০৪,২০০১; চঃ ২০০১; টেক্সটাইলঃ ২০০৯-২০১০
\(Ex.14.\) \(O\) বিন্দুতে ক্রিয়ারত \(P\) ও \(Q\) বলদ্বয়ের লব্ধি \(R\) একটি সরলরেখা তাদের ক্রিয়ারেখাগুলিকে যথাক্রমে \(L, M, N\) বিন্দুতে ছেদ করলে প্রমাণ কর যে, \(\frac{P}{OL}+\frac{Q}{OM}=\frac{R}{ON}\).
রাঃ ২০১৪; যঃ ২০০৮; চঃ ২০০৬,২০০২; রুয়েটঃ২০১১-২০১২
\(Ex.15.\) \(1, 2, 3, 4, 5 \) কেজি ওজনের বলগুলি কোন সুষম ষড়ভুজের একটি কৌণিক বিন্দু থেকে যথাক্রমে অপর কৌণিক বিন্দুগুলির দিকে ক্রিয়ারত আছে। এদের লব্ধি নির্ণয় কর।
উত্তরঃ \(2\sqrt{19+10\sqrt{3}}\)
উত্তরঃ \(2\sqrt{19+10\sqrt{3}}\)
\(Ex.16.\) যদি \(ABCD\) চতুর্ভুজের \(AB, \ BC, \ CD, \ DA\) বাহু চতুষ্টয়ের মধ্যবিন্দু যথাক্রমে \(E, \ F, \ G\) ও \(H\) এর তলে \(O\) যে কোনো একটি বিন্দু। দেখাও যে, \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OE}+\overrightarrow{OF}+\overrightarrow{OG}+\overrightarrow{OH}\)
\(Ex.17.\) একটি বৃত্তের \(AB\) ও \(AC\) দুইটি জ্যা দ্বারা সূচীত দুইটি বলের লব্ধি বৃত্তের কেন্দ্রগামী হলে প্রমাণ কর যে, বল দুইটি সমান অথবা পরস্পর লম্ব।
\(Ex.18.\) \(7\) ও \(8\) কিলোগ্রাম ওজনের দুইটি বলের লব্ধি \(13\) কিলোগ্রাম হলে বলদ্বয়ের মধ্যবর্তী কোণ ও দিক নির্ণয় কর।
উত্তরঃ \(60^{o}, \ \tan^{-1}{\frac{4\sqrt{3}}{11}}\)
উত্তরঃ \(60^{o}, \ \tan^{-1}{\frac{4\sqrt{3}}{11}}\)
\(Ex.19.\)
চিত্র থেকে পরস্পর লম্ব দিকে \(10 N\) বলের আনুভূমিক ও উল্লম্ব উপাংশ নির্ণয় কর।
উত্তরঃ \(5\sqrt{3} N, \ 5 N\)
চিত্র থেকে পরস্পর লম্ব দিকে \(10 N\) বলের আনুভূমিক ও উল্লম্ব উপাংশ নির্ণয় কর।
উত্তরঃ \(5\sqrt{3} N, \ 5 N\)

Q.2-এর বর্ণনামূলক প্রশ্নসমূহ
Q.3-এর বর্ণনামূলক প্রশ্নসমূহ
Q.4-এর বর্ণনামূলক প্রশ্নসমূহ
Q.5-এর সৃজনশীল প্রশ্নসমূহ
ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000003